北师大版七年级数学下册第三章变量之间的关系同步单元练习(含答案)
文档属性
| 名称 | 北师大版七年级数学下册第三章变量之间的关系同步单元练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 105.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-29 12:16:04 | ||
图片预览


文档简介
第3章 变量之间的关系
一.选择题(共10小题)
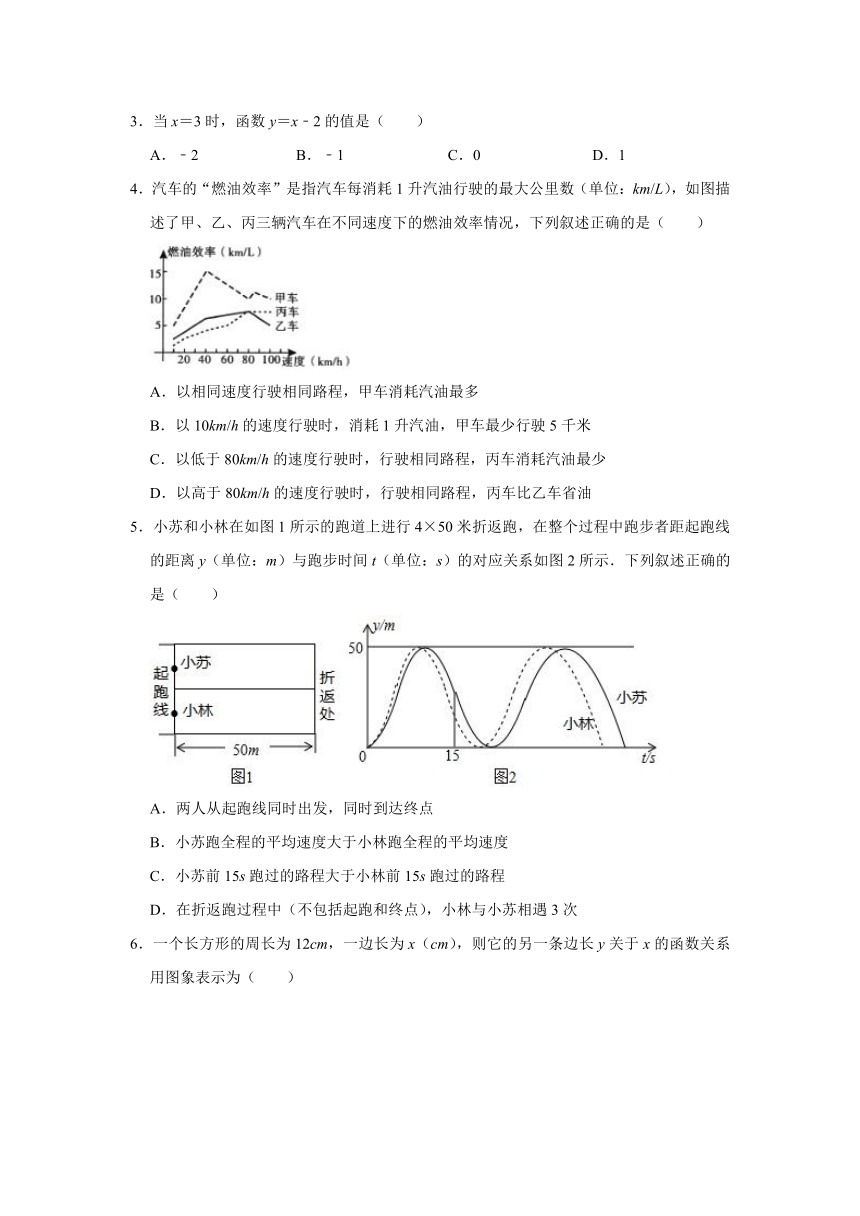
1.函数y=|x|﹣1中的自变量x的取值范围是( )
A.x≠±1 B.x≠1
C.x≠﹣1 D.x为全体实数
2.下列各曲线中,表示y是x的函数的是( )
A.
B.
C.
D.
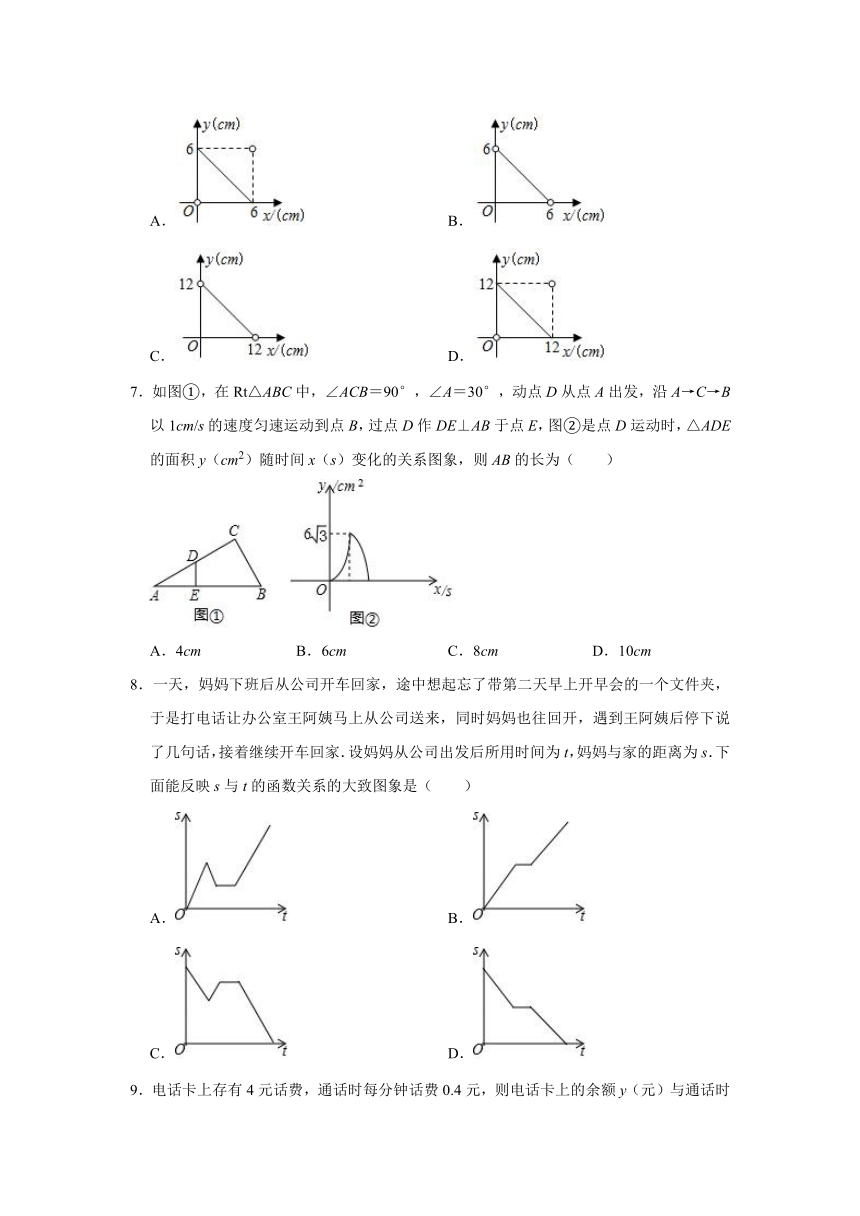
3.当x=3时,函数y=x﹣2的值是( )
A.﹣2 B.﹣1 C.0 D.1
4.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
A.以相同速度行驶相同路程,甲车消耗汽油最多
B.以10km/h的速度行驶时,消耗1升汽油,甲车最少行驶5千米
C.以低于80km/h的速度行驶时,行驶相同路程,丙车消耗汽油最少
D.以高于80km/h的速度行驶时,行驶相同路程,丙车比乙车省油
5.小苏和小林在如图1所示的跑道上进行4×50米折返跑,在整个过程中跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图2所示.下列叙述正确的是( )
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15s跑过的路程大于小林前15s跑过的路程
D.在折返跑过程中(不包括起跑和终点),小林与小苏相遇3次
6.一个长方形的周长为12cm,一边长为x(cm),则它的另一条边长y关于x的函数关系用图象表示为( )
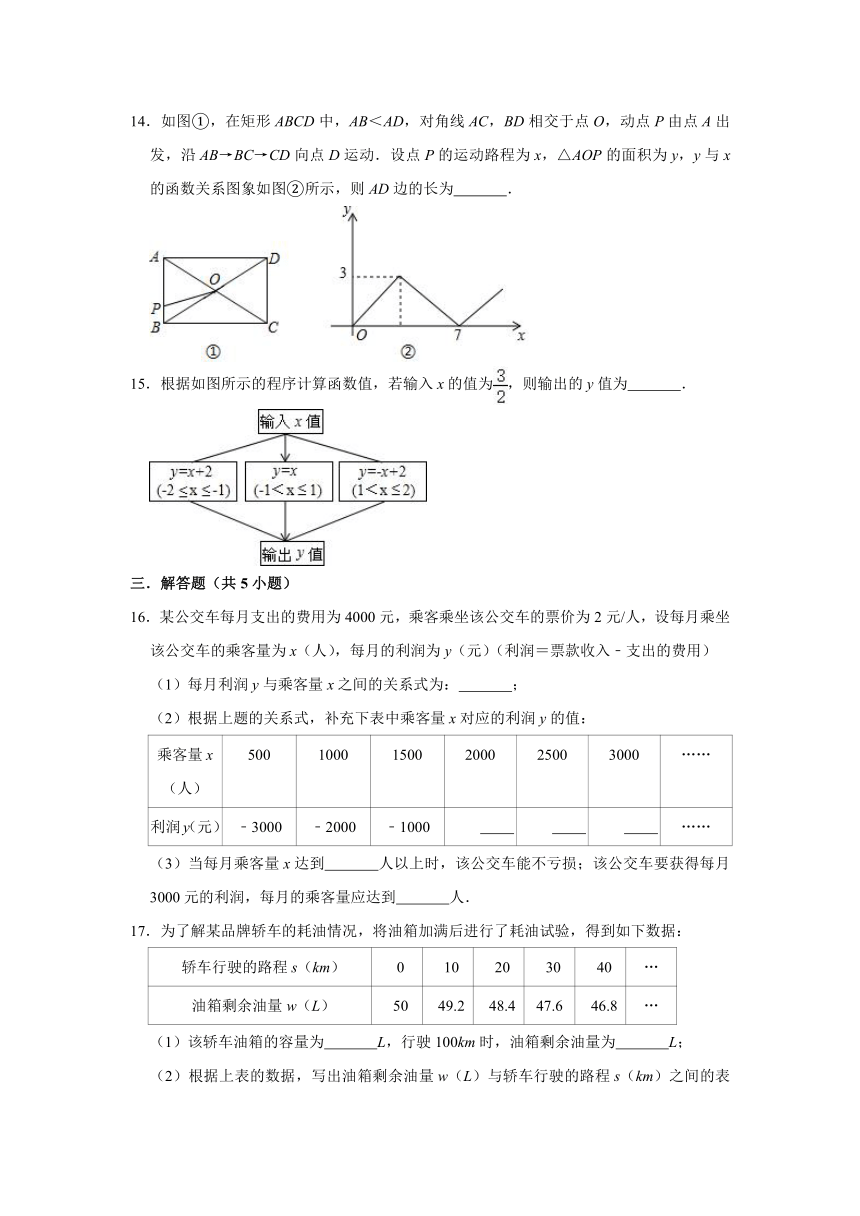
A. B.
C. D.
7.如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,动点D从点A出发,沿A→C→B以1cm/s的速度匀速运动到点B,过点D作DE⊥AB于点E,图②是点D运动时,△ADE的面积y(cm2)随时间x(s)变化的关系图象,则AB的长为( )
A.4cm B.6cm C.8cm D.10cm
8.一天,妈妈下班后从公司开车回家,途中想起忘了带第二天早上开早会的一个文件夹,于是打电话让办公室王阿姨马上从公司送来,同时妈妈也往回开,遇到王阿姨后停下说了几句话,接着继续开车回家.设妈妈从公司出发后所用时间为t,妈妈与家的距离为s.下面能反映s与t的函数关系的大致图象是( )
A. B.
C. D.
9.电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A. B.
C. D.
10.某厂前5个月生产的总产量y(件)与时间x(月)的关系如图所示,则下列说法正确的是( )
A.1﹣3月的月产量逐月增加,4、5两月产量逐月减少
B.1﹣3月的月产量逐月增加,4、5两月产量与3月持平
C.1﹣3月的月产量逐月增加,4、5两月停产
D.1﹣3月的月产量逐月持平,4、5两月停产
二.填空题(共5小题)
11.图书馆现有1500本图书供学生借阅,如果每个学生一次借3本,则剩下的数y(本)和借书学生人数x(人)之间的函数关系式是 .
12.点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分
0
2
4
6
8
10
h/厘米
30
29
28
27
26
25
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式 ;这根蜡烛最多能燃烧的时间为 分.
13.归纳观察图象的方法:
①当x>0时?观察 的函数图象;当x<0时?观察 的函数图象.
②当y>0时?观察 的函数图象;当y<0时?观察 的函数图象.
14.如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动.设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AD边的长为 .
15.根据如图所示的程序计算函数值,若输入x的值为,则输出的y值为 .
三.解答题(共5小题)
16.某公交车每月支出的费用为4000元,乘客乘坐该公交车的票价为2元/人,设每月乘坐该公交车的乘客量为x(人),每月的利润为y(元)(利润=票款收入﹣支出的费用)
(1)每月利润y与乘客量x之间的关系式为: ;
(2)根据上题的关系式,补充下表中乘客量x对应的利润y的值:
乘客量x(人)
500
1000
1500
2000
2500
3000
……
利润y(元)
﹣3000
﹣2000
﹣1000
……
(3)当每月乘客量x达到 人以上时,该公交车能不亏损;该公交车要获得每月3000元的利润,每月的乘客量应达到 人.
17.为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如下数据:
轿车行驶的路程s(km)
0
10
20
30
40
…
油箱剩余油量w(L)
50
49.2
48.4
47.6
46.8
…
(1)该轿车油箱的容量为 L,行驶100km时,油箱剩余油量为 L;
(2)根据上表的数据,写出油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式 ;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.
18.如图,在四边形APBE中,AB为对角线,C是边AE上一动点,连接PC交AB于点D.设B,D两点间的距离为xcm,P,C两点间的距离为y1cm,P,D两点间的距离为y2cm.
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究,下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值,如下表:
位置1
位置2
位置3
位置4
位置5
位置6
位置7
y1/cm
9.68
9.26
7.79
6.09
5.54
4.93
4.72
y2/cm
4.08
4.03
3.88
3.74
3.76
3.99
4.72
x/cm
5.00
5.11
5.60
6.50
7.00
8.00
9.50
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数关系的图象m,n如下:
其中能表示y1与x的函数关系的图象大致是 ;
其中能表示y2与x的函数关系的图象大致是 .
(3)解决问题:当x=6时可知P,C两点间的距离 P,D两点间的距离(填“>“,“=“,“<“)
19.如图.正方形ABCD的边长为4cm.P为DC上的点,当点P从C向D移动时,四边形APCB的面积发生了变化.
(1)设线段CP长为x,则△APD的面积y可以表示为 ;
(2)这个变化过程中,自变量是 ,因变量是 ;
(3)当线段CP从1cm增加到3cm时,△APD的面积减小了多少?
20.将长为40cm、宽为15cm的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为5cm.
(1)根据上图,将表格补充完整:
白纸张数
1
2
3
4
…
10
…
纸条长度
40
75
110
…
…
(2)设x张白纸黏合后的总长度为ycm,则y与x之间的关系式是 ;
(3)你认为白纸黏合起来总长度可能为2018cm吗?为什么?
参考答案
一.选择题(共10小题)
1. D.
2. D.
3. D.
4.D.
5. D.
6. B.
7. C.
8. C.
9. D.
10. D.
二.填空题(共5小题)
11. y=1500﹣3x.
12. y=30﹣0.5t,60.
13. x轴上方,x轴下方.
14. 4.
15. .
三.解答题(共5小题)
16.解:(1)每月利润y与乘客量x之间的关系式为y=2x﹣4000,
故答案为:y=2x﹣4000;
(2)当x=2000时,y=2×2000﹣4000=0,
当x=2500时,y=2×2500﹣4000=1000,
当x=3000时,y=2×3000﹣4000=2000,
故答案为:0;1000;2000;
(3)当每月乘客量x达到2000人以上时,该公交车能不亏损;
设公交车要获得每月3000元的利润,每月的乘客量应达到x人,
由题意得,2x﹣4000=3000,
解得,x=3500,
故答案为:3500.
17.解:(1)由表格中的数据可知,该轿车油箱的容量为50L,行驶100km时,油箱剩余油量为:50﹣×0.8=42(L).、
故答案是:50;42;
(2)由表格可知,开始油箱中的油为50L,每行驶10km,油量减少0.8L,据此可得w与s的关系式为w=50﹣0.08s;
故答案是:w=50﹣0.08s;
(3)令w=26,得s=300.
答:A,B两地之间的距离为300km.
18.解:(2)由图象可得:表示y1与x的函数关系的图象大致是m,表示y2与x的函数关系的图象大致是n,
故答案为:m,n;
(3)由图象可得:当x=6时,图象m在图象n的上方,
∴P,C两点间的距离>P,D两点间的距离,
故答案为:>.
19.解:(1)因为线段CP长为x,则DP=CD﹣CP=4﹣x(cm),
根据△APD的面积=,
∴=8﹣2x.
(2)在这个变化过程中,自变量是x,因变量是y;
(3)当CP=1cm时,y=8﹣2×1=6(cm2),
当CP=3cm时,y=8﹣2×3=2(cm2),
6﹣2=4(cm2),
所以△APD的面积减少了4cm2.
20.解:(1)填表如下:
白纸张数
1
2
3
4
…
10
…
纸条长度
40
75
110
145
…
355
…
(2)设x张白纸黏合后的总长度为ycm,则y与x之间的关系式是y=40x﹣5(x﹣1)=35x+5.
(3)不能.
把y=2018代入y=35x+5,得35x+5=2018
解得57,不是整数,
所以不能.
故答案为:y=35x+5.
一.选择题(共10小题)
1.函数y=|x|﹣1中的自变量x的取值范围是( )
A.x≠±1 B.x≠1
C.x≠﹣1 D.x为全体实数
2.下列各曲线中,表示y是x的函数的是( )
A.
B.
C.
D.
3.当x=3时,函数y=x﹣2的值是( )
A.﹣2 B.﹣1 C.0 D.1
4.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )
A.以相同速度行驶相同路程,甲车消耗汽油最多
B.以10km/h的速度行驶时,消耗1升汽油,甲车最少行驶5千米
C.以低于80km/h的速度行驶时,行驶相同路程,丙车消耗汽油最少
D.以高于80km/h的速度行驶时,行驶相同路程,丙车比乙车省油
5.小苏和小林在如图1所示的跑道上进行4×50米折返跑,在整个过程中跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图2所示.下列叙述正确的是( )
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15s跑过的路程大于小林前15s跑过的路程
D.在折返跑过程中(不包括起跑和终点),小林与小苏相遇3次
6.一个长方形的周长为12cm,一边长为x(cm),则它的另一条边长y关于x的函数关系用图象表示为( )
A. B.
C. D.
7.如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,动点D从点A出发,沿A→C→B以1cm/s的速度匀速运动到点B,过点D作DE⊥AB于点E,图②是点D运动时,△ADE的面积y(cm2)随时间x(s)变化的关系图象,则AB的长为( )
A.4cm B.6cm C.8cm D.10cm
8.一天,妈妈下班后从公司开车回家,途中想起忘了带第二天早上开早会的一个文件夹,于是打电话让办公室王阿姨马上从公司送来,同时妈妈也往回开,遇到王阿姨后停下说了几句话,接着继续开车回家.设妈妈从公司出发后所用时间为t,妈妈与家的距离为s.下面能反映s与t的函数关系的大致图象是( )
A. B.
C. D.
9.电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A. B.
C. D.
10.某厂前5个月生产的总产量y(件)与时间x(月)的关系如图所示,则下列说法正确的是( )
A.1﹣3月的月产量逐月增加,4、5两月产量逐月减少
B.1﹣3月的月产量逐月增加,4、5两月产量与3月持平
C.1﹣3月的月产量逐月增加,4、5两月停产
D.1﹣3月的月产量逐月持平,4、5两月停产
二.填空题(共5小题)
11.图书馆现有1500本图书供学生借阅,如果每个学生一次借3本,则剩下的数y(本)和借书学生人数x(人)之间的函数关系式是 .
12.点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分
0
2
4
6
8
10
h/厘米
30
29
28
27
26
25
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式 ;这根蜡烛最多能燃烧的时间为 分.
13.归纳观察图象的方法:
①当x>0时?观察 的函数图象;当x<0时?观察 的函数图象.
②当y>0时?观察 的函数图象;当y<0时?观察 的函数图象.
14.如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动.设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AD边的长为 .
15.根据如图所示的程序计算函数值,若输入x的值为,则输出的y值为 .
三.解答题(共5小题)
16.某公交车每月支出的费用为4000元,乘客乘坐该公交车的票价为2元/人,设每月乘坐该公交车的乘客量为x(人),每月的利润为y(元)(利润=票款收入﹣支出的费用)
(1)每月利润y与乘客量x之间的关系式为: ;
(2)根据上题的关系式,补充下表中乘客量x对应的利润y的值:
乘客量x(人)
500
1000
1500
2000
2500
3000
……
利润y(元)
﹣3000
﹣2000
﹣1000
……
(3)当每月乘客量x达到 人以上时,该公交车能不亏损;该公交车要获得每月3000元的利润,每月的乘客量应达到 人.
17.为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如下数据:
轿车行驶的路程s(km)
0
10
20
30
40
…
油箱剩余油量w(L)
50
49.2
48.4
47.6
46.8
…
(1)该轿车油箱的容量为 L,行驶100km时,油箱剩余油量为 L;
(2)根据上表的数据,写出油箱剩余油量w(L)与轿车行驶的路程s(km)之间的表达式 ;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.
18.如图,在四边形APBE中,AB为对角线,C是边AE上一动点,连接PC交AB于点D.设B,D两点间的距离为xcm,P,C两点间的距离为y1cm,P,D两点间的距离为y2cm.
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究,下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值,如下表:
位置1
位置2
位置3
位置4
位置5
位置6
位置7
y1/cm
9.68
9.26
7.79
6.09
5.54
4.93
4.72
y2/cm
4.08
4.03
3.88
3.74
3.76
3.99
4.72
x/cm
5.00
5.11
5.60
6.50
7.00
8.00
9.50
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数关系的图象m,n如下:
其中能表示y1与x的函数关系的图象大致是 ;
其中能表示y2与x的函数关系的图象大致是 .
(3)解决问题:当x=6时可知P,C两点间的距离 P,D两点间的距离(填“>“,“=“,“<“)
19.如图.正方形ABCD的边长为4cm.P为DC上的点,当点P从C向D移动时,四边形APCB的面积发生了变化.
(1)设线段CP长为x,则△APD的面积y可以表示为 ;
(2)这个变化过程中,自变量是 ,因变量是 ;
(3)当线段CP从1cm增加到3cm时,△APD的面积减小了多少?
20.将长为40cm、宽为15cm的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为5cm.
(1)根据上图,将表格补充完整:
白纸张数
1
2
3
4
…
10
…
纸条长度
40
75
110
…
…
(2)设x张白纸黏合后的总长度为ycm,则y与x之间的关系式是 ;
(3)你认为白纸黏合起来总长度可能为2018cm吗?为什么?
参考答案
一.选择题(共10小题)
1. D.
2. D.
3. D.
4.D.
5. D.
6. B.
7. C.
8. C.
9. D.
10. D.
二.填空题(共5小题)
11. y=1500﹣3x.
12. y=30﹣0.5t,60.
13. x轴上方,x轴下方.
14. 4.
15. .
三.解答题(共5小题)
16.解:(1)每月利润y与乘客量x之间的关系式为y=2x﹣4000,
故答案为:y=2x﹣4000;
(2)当x=2000时,y=2×2000﹣4000=0,
当x=2500时,y=2×2500﹣4000=1000,
当x=3000时,y=2×3000﹣4000=2000,
故答案为:0;1000;2000;
(3)当每月乘客量x达到2000人以上时,该公交车能不亏损;
设公交车要获得每月3000元的利润,每月的乘客量应达到x人,
由题意得,2x﹣4000=3000,
解得,x=3500,
故答案为:3500.
17.解:(1)由表格中的数据可知,该轿车油箱的容量为50L,行驶100km时,油箱剩余油量为:50﹣×0.8=42(L).、
故答案是:50;42;
(2)由表格可知,开始油箱中的油为50L,每行驶10km,油量减少0.8L,据此可得w与s的关系式为w=50﹣0.08s;
故答案是:w=50﹣0.08s;
(3)令w=26,得s=300.
答:A,B两地之间的距离为300km.
18.解:(2)由图象可得:表示y1与x的函数关系的图象大致是m,表示y2与x的函数关系的图象大致是n,
故答案为:m,n;
(3)由图象可得:当x=6时,图象m在图象n的上方,
∴P,C两点间的距离>P,D两点间的距离,
故答案为:>.
19.解:(1)因为线段CP长为x,则DP=CD﹣CP=4﹣x(cm),
根据△APD的面积=,
∴=8﹣2x.
(2)在这个变化过程中,自变量是x,因变量是y;
(3)当CP=1cm时,y=8﹣2×1=6(cm2),
当CP=3cm时,y=8﹣2×3=2(cm2),
6﹣2=4(cm2),
所以△APD的面积减少了4cm2.
20.解:(1)填表如下:
白纸张数
1
2
3
4
…
10
…
纸条长度
40
75
110
145
…
355
…
(2)设x张白纸黏合后的总长度为ycm,则y与x之间的关系式是y=40x﹣5(x﹣1)=35x+5.
(3)不能.
把y=2018代入y=35x+5,得35x+5=2018
解得57,不是整数,
所以不能.
故答案为:y=35x+5.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
