人教版八年级下册数学17.1勾股定理课件:20PPT
文档属性
| 名称 | 人教版八年级下册数学17.1勾股定理课件:20PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-30 23:30:46 | ||
图片预览








文档简介
(共20张PPT)
勾股定理
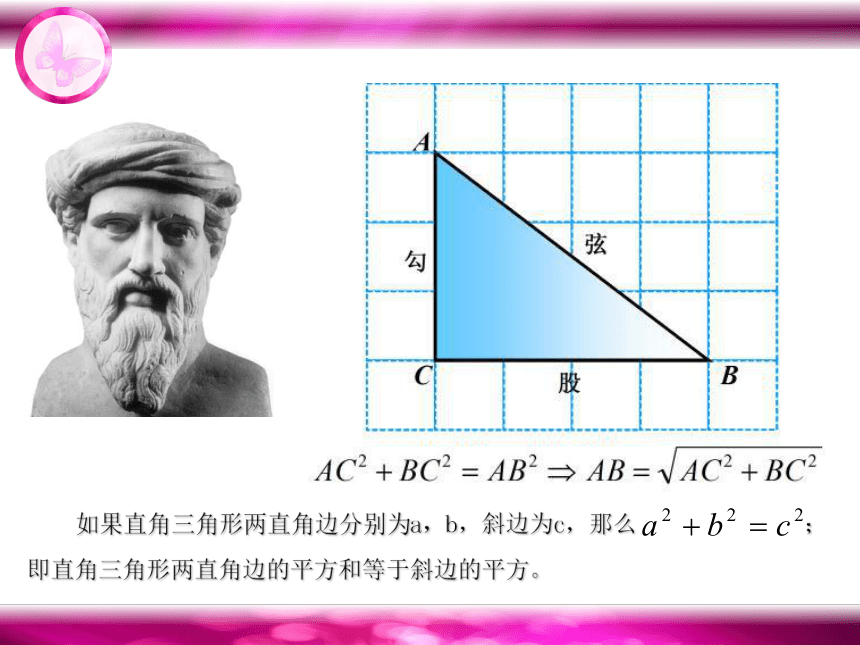
如果直角三角形两直角边分别为a,b,斜边为c,那么 ; 即直角三角形两直角边的平方和等于斜边的平方。
勾股定理的证明
证明方法:拼三角形
同学们动手一起拼
利用拼图来验证勾股定理:
1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边为c);
2、你能用这四个直角三角形拼成一个以斜边c正方形吗?拼一拼试试看?
3.你能否就你拼出的图说明a2+b2=c2?
∵ c2= 4?ab/2 +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4?ab/2-(b- a)2
∵ (a+b)2 = c2 + 4?ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4?ab/2
勾股定理的证明
证明方法:赵爽弦图,动手拼图
勾股定理的证明
证明方法:美国总统加菲尔德的证明方法
在直角三角形中,已知两边可以求第三边
例1 如图,在Rt△ABC中,BC=24,AC=7,求AB的长。
在Rt△ABC中
, 根据勾股定理
解:
例2 已知等边三角形ABC的边长是6cm, (1)求高AD的长;(2)S△ABC
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
, 根据勾股定理
例3 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
练习
1.在△ABC中,∠C=90°.
(1)若a=6,c=10,则b= ;
(2)若a=12,b=9,则c= ;
3.如图,在△ABC中,C=90°,CD为斜边AB上的高,你可以得出哪些与边有关的结论?
(3)若c=25,b=15,则a= ;
20
2.等边三角形边长为10,求它的高及面积。
b
a
如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么 ; 即直角三角形两直角边的平方和等于斜边的平方。
勾股定理的证明
证明方法:拼三角形
同学们动手一起拼
利用拼图来验证勾股定理:
1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边为c);
2、你能用这四个直角三角形拼成一个以斜边c正方形吗?拼一拼试试看?
3.你能否就你拼出的图说明a2+b2=c2?
∵ c2= 4?ab/2 +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4?ab/2-(b- a)2
∵ (a+b)2 = c2 + 4?ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
c2 +4?ab/2
勾股定理的证明
证明方法:赵爽弦图,动手拼图
勾股定理的证明
证明方法:美国总统加菲尔德的证明方法
在直角三角形中,已知两边可以求第三边
例1 如图,在Rt△ABC中,BC=24,AC=7,求AB的长。
在Rt△ABC中
, 根据勾股定理
解:
例2 已知等边三角形ABC的边长是6cm, (1)求高AD的长;(2)S△ABC
解:(1)
∵△ABC是等边三角形,AD是高
在Rt△ABD中
, 根据勾股定理
例3 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
练习
1.在△ABC中,∠C=90°.
(1)若a=6,c=10,则b= ;
(2)若a=12,b=9,则c= ;
3.如图,在△ABC中,C=90°,CD为斜边AB上的高,你可以得出哪些与边有关的结论?
(3)若c=25,b=15,则a= ;
20
2.等边三角形边长为10,求它的高及面积。
b
a
如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
