江苏省昆山市石牌中学2019-2020学年第二学期苏科版八年级数学第11章《反比例函数》自主学习检测 含答案
文档属性
| 名称 | 江苏省昆山市石牌中学2019-2020学年第二学期苏科版八年级数学第11章《反比例函数》自主学习检测 含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 362.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-29 00:00:00 | ||
图片预览

文档简介
《反比例函数》自主学习检测
一、单选题(共10题;共30分)
1.下列函数中,反比例函数是 (???? )
A.;????????B.?;????????C.?;????????D.?
2.点A(3,2)在反比例函数?(x>0),则点B的坐标不可能的是( ? ? )
A.?(2,3);????B.??;??????????C.??;???????????D.?;
3.反比例函数y=的图象,当x>0时,y随x的增大而增大,则k的取值范围是(?? )
A.?k<3?????????????????????????????????????B.?k≤3?????????????????????????????????????C.?k>3?????????????????????????????????????D.?k≥3
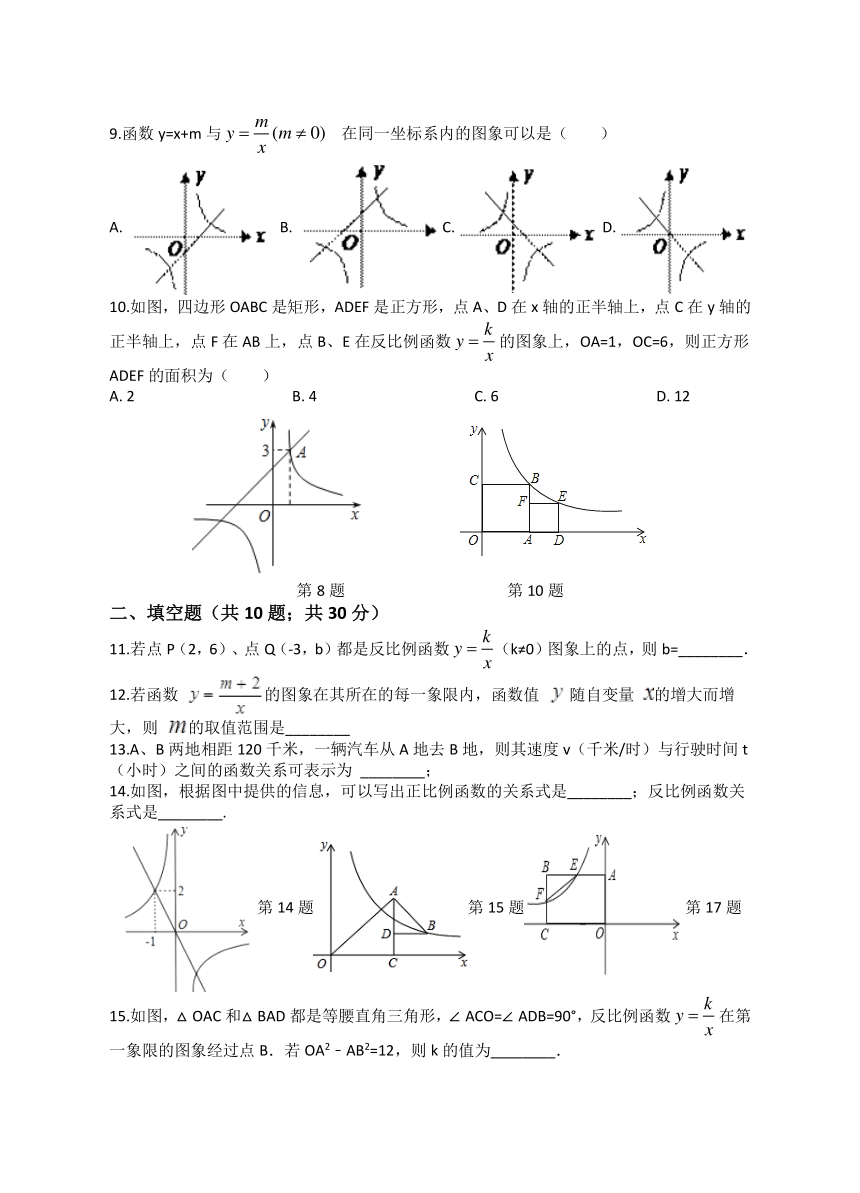
第2题第4题第6题
4.如图,双曲线y= 的一个分支为(?? )
A.?①;?????????????????B.?②;????????????????????C.?③?;????????????????D.?④
5.已知甲、乙两地相距 (km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(h)与行驶速度 (km/h)的函数关系图像大致是(?? )
A.??C.??D.?
6.如图,矩形OABC上,点A、C分别在x、y轴上,点B在反比例位于第二象限的图象上,矩形面积为6,则k的值是(?? )
A.?3?????????????????????????????????????????B.?6?????????????????????????????????????????C.?﹣6?????????????????????????????????????????D.?﹣3
7.已知点A(x1 , y1)、B(x2 , y2)是反比例函数y=﹣图象上的两点,若x2<0<x1 , 则有(?? )
A.?0<y1<y2????????????????????????B.?0<y2<y1????????????????????????C.?y2<0<y1????????????????????????D.?y1<0<y2
8.如图,直线y=x+2与双曲线相交于点A,点A的纵坐标为3,k的值为( )
A.?1 ??????????????????????????????????????B.?2??????????????????????????????????????C.?3 ??????????????????????????????????????D.?4
9.函数y=x+m与 ?在同一坐标系内的图象可以是(? ? )
A.???B.?C.??D.?
10.如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数的图象上,OA=1,OC=6,则正方形ADEF的面积为( )
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?6???????????????????????????????????????????D.?12
第8题 第10题
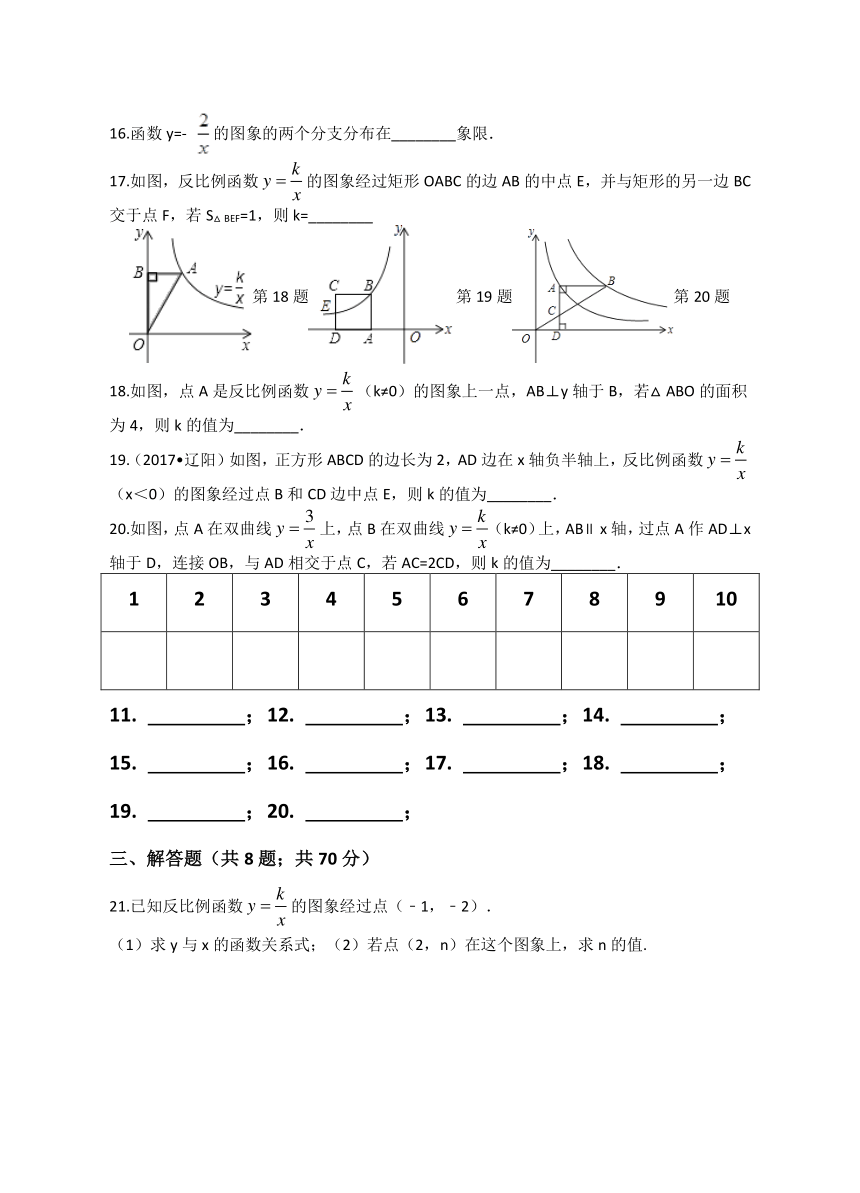
二、填空题(共10题;共30分)
11.若点P(2,6)、点Q(-3,b)都是反比例函数(k≠0)图象上的点,则b=________.
12.若函数 的图象在其所在的每一象限内,函数值 随自变量 的增大而增大,则 的取值范围是________
13.A、B两地相距120千米,一辆汽车从A地去B地,则其速度v(千米/时)与行驶时间t(小时)之间的函数关系可表示为 ________;
14.如图,根据图中提供的信息,可以写出正比例函数的关系式是________;反比例函数关系式是________.
第14题第15题第17题
15.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数在第一象限的图象经过点B.若OA2﹣AB2=12,则k的值为________.
16.函数y=- 的图象的两个分支分布在________象限.
17.如图,反比例函数的图象经过矩形OABC的边AB的中点E,并与矩形的另一边BC交于点F,若S△BEF=1,则k=________
第18题第19题第20题
18.如图,点A是反比例函数(k≠0)的图象上一点,AB⊥y轴于B,若△ABO的面积为4,则k的值为________.
19.(2017?辽阳)如图,正方形ABCD的边长为2,AD边在x轴负半轴上,反比例函数(x<0)的图象经过点B和CD边中点E,则k的值为________.
20.如图,点A在双曲线上,点B在双曲线(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D,连接OB,与AD相交于点C,若AC=2CD,则k的值为________.
1 2 3 4 5 6 7 8 9 10
11. ;12. ;13. ;14. ;15. ;16. ;17. ;18. ;19. ;20. ;
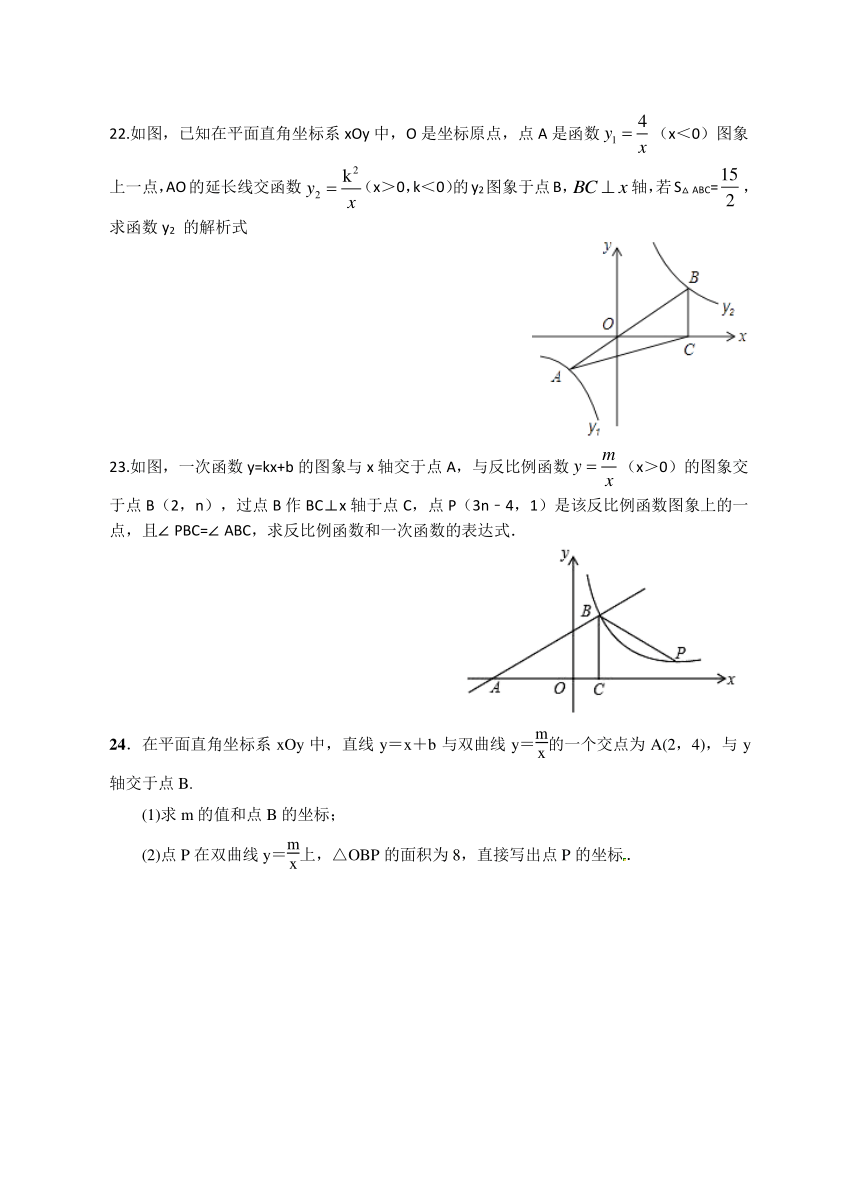
三、解答题(共8题;共70分)
21.已知反比例函数的图象经过点(﹣1,﹣2).
(1)求y与x的函数关系式;(2)若点(2,n)在这个图象上,求n的值.
22.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数(x<0)图象上一点,AO的延长线交函数(x>0,k<0)的y2图象于点B,轴,若S△ABC=,求函数y2 的解析式
23.如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
24.在平面直角坐标系xOy中,直线y=x+b与双曲线y=的一个交点为A(2,4),与y轴交于点B.
(1)求m的值和点B的坐标;
(2)点P在双曲线y=上,△OBP的面积为8,直接写出点P的坐标.
25.已知反比例函数y=.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
(第25题)
26.如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,AC∥x轴,A、B两点在反比例函数(x>0)的图象上,延长CA交y轴于点D,AD=1.
(1)求该反比例函数的解析式;
(2)将△ABC绕点B顺时针旋转得到△EBF,使点C落在x轴上的点F处,点A的对应点为E,求旋转角的度数和点E的坐标.
27.如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若S△BOD=4,请回答下列问题:
(1)求反比例函数解析式;
(2)求C点坐标.
28.如图,已知一次函数y=x﹣3与反比例函数的图象相交于点A(4,n),与轴相交于点B.
(1)填空:n的值为________,k的值为________;
(2)以AB为边作菱形ABCD,使点C在 轴正半轴上,点D在第一象限,求点D的坐标;
(3)考察反比函数的图象,当时,请直接写出自变量的取值范围.
答案解析部分
一、单选题
1.【答案】B 2.【答案】C 3.【答案】A 4.【答案】D 5.【答案】C 6.【答案】C
7.【答案】D 8.【答案】C 9.【答案】B 10.【答案】B
二、填空题
11.【答案】-4 12.【答案】m<-2 13.【答案】v =14.【答案】y=-2x;
15.【答案】6 16.【答案】二、四 17.【答案】-4 18.【答案】8
19.【答案】﹣4 20.【答案】9
三、解答题
21.【答案】解:(1)∵点(﹣1,﹣2)在反比例函数上,∴k=﹣1×(﹣2)=2,
∴y与x的函数关系式为.
(2)∵点(2,n)在这个图象上,∴2n=2,∴n=1.
22.【答案】解:设A(m, )(m<0), 直线AB的解析式为y=ax(k≠0),
∵A(m, ),∴ma= ,解得a= ,∴直线AB的解析式为y= x.
∵AO的延长线交函数y= 的图象于点B,∴B(﹣ mk,﹣ ),
∵△ABC的面积等于 ,CB⊥x轴,∴ ×(﹣ )×(﹣ mk+|m|)= ,
解得k1=﹣5(舍去),k2=3,∴y2=
23.【答案】解:∵点B(2,n)、P(3n﹣4,1)在反比例函数(x>0)的图象上,∴ .解得 .∴反比例函数解析式:,∴点B(2,4),(8,1).过点P作PD⊥BC,垂足为D,并延长交AB与点P′.在△BDP和△BDP′中,
,∴△BDP≌△BDP′.∴DP′=DP=6.∴点P′(﹣4,1).
∴ ,解得: .∴一次函数的表达式为y=x+3.
24.解:(1)∵双曲线y=经过点A(2,4),∴m=8.
∵直线y=x+b经过点A(2,4),∴b=2.
∴此直线与y轴的交点B的坐标为(0,2).
(2)点P的坐标为(8,1)或(-8,-1).
25.解:(1)联立方程组得kx2+4x-4=0.∵反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,∴Δ=16+16k=0,∴k=-1.
(2)如图所示,C1平移至C2处所扫过的面积为2×3=6.
(第25题)
26.【答案】解:(1)∵AC∥x轴,AD=1,∴A(1,k),
∵∠C=90°,AC=2,BC=4,∴B(3,k﹣4),
∵点B在的图象上,∴3(k﹣4)=k,解得k=6,
∴该反比例函数的解析式为y=;
(2)作BM⊥x轴于M,EN⊥x轴于N,如图,
∵△ABC绕点B顺时针旋转得到△EBF,
∴BF=BC=4,EF=AC=2,∠BFE=∠BCA=90°,∠CBF等于旋转角,
∵BC⊥x轴,A(1,6),∴BM=CM﹣BC=6﹣4=2,
在Rt△BMF中,∵cos∠MBF===,∴∠MBF=60°,MF=BM=,
∴∠CBF=180°﹣∠MBF=120°,∴旋转角为120°;
∵∠BFM+∠MBF=90°,∠BFM+∠EFN=90°,∴∠MBF=∠EFN,∴Rt△BMF∽Rt△FNE,
∴==,即==,∴FN=1,EN=,∴ON=OM+MF+FN=1++1=2+,
∴E点坐标为(2+,).
27.【答案】(1)解:∵∠ABO=90°,S△BOD=4,∴ ×k=4,解得k=8,
∴反比例函数解析式为 ;
(2)解:∵∠ABO=90°,OB=4,AB=8,∴A点坐标为(4,8),
设直线OA的解析式为y=kx,把A(4,8)代入得4k=8,解得k=2,
∴直线OA的解析式为y=2x,解方程组 ,得 或 ,
∵C在第一象限,∴C点坐标为(2,4).
28.【答案】(1)解:把点A(4,n)代入一次函数y=x﹣3,可得n=×4﹣3=3;;把点A(4,3)代入反比例函数y= , 可得3= , 解得k=12;
(2)解:∵一次函数y=x﹣3与x轴相交于点B,???? ∴x﹣3=0,解得x=2,
∴点B的坐标为(2,0);
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),∴OE=4,AE=3,OB=2,∴BE=OE﹣OB=4﹣2=2,
在Rt△ABE中,AB===,
∵四边形ABCD是菱形,∴AB=CD=BC=,
∵AB∥CD,∴∠ABE=∠DCF,∵AE⊥x轴,DF⊥x轴,∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3;∴OF=OB+BC+CF=2++2=4+,∴点D的坐标为(4+,3)
(3)解:当y=﹣2时,﹣2=,解得x=﹣6.
故当y≥﹣2时,自变量x的取值范围是x≤﹣6或x>0.
学校 班级 姓名 考试号
-----------------------------------------------------------密---------------------------------封----------------------------------线--------------------------------------
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
