人教版高一物理必修2第七章 7.1追寻守恒量——能量(共31张PPT)
文档属性
| 名称 | 人教版高一物理必修2第七章 7.1追寻守恒量——能量(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 32.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-29 16:04:06 | ||
图片预览








文档简介
(共31张PPT)
第1节 追寻守恒量——能量
找棋子
放学后,两个小孩在家中下象棋。下完棋后,当他们收拾象棋时,忽然发现少了3颗棋子,他们找啊找,发现门后有1颗,墙角有1颗,但还是少1颗。他们不放弃,继续寻找,终于在地毯下找到了最后1颗棋子。
问题:支撑两个小孩能够坚持找到最后1颗棋子的信念是什么?
棋子的数量守恒
[案例一]
查水表
自来水公司抄表员最近发现,某小区一单元楼的自来水管道的总表读数和各住户家中分表读数总和不一致。对于这个问题,你有什么想法?
问题:支撑你们有这些想法的依据是什么?
水的体积守恒
[案例二]
沙漏
装有沙子的封闭沙漏,细砂从A中流入B中。A、B中沙子的总质量如何变化?
问题:支撑你们有这种想法的依据是什么?
沙漏中沙子的质量守恒
A
B
[案例三]
化学反应方程式
Fe+2Fe3+= 3Fe2+
问题:配平化学方程式的依据是什么?
原子数守恒、电荷守恒
[案例四]
物理学的任务是发现普遍的自然规律。因为这样的规律的最简单的形式之一表现为某种物理量的不变性,所以对于守恒量的寻求不仅是合理的,而且也是极为重要的研究方向。
——劳厄
(1879-1960德国)
物理学家,1912年发现晶体的X射线衍射现象,并因此获得诺贝尔物理学奖
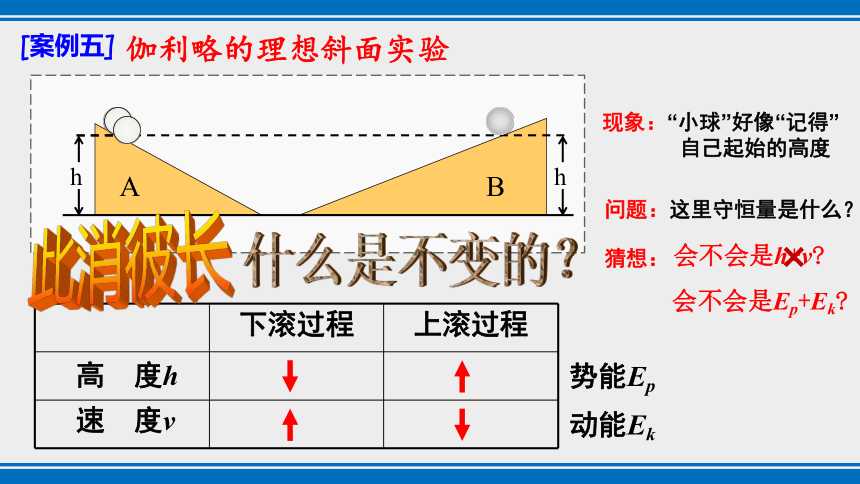
伽利略的理想斜面实验
[案例五]
A
B
h
h
下滚过程 上滚过程
高 度h
速 度v
此消彼长
现象:“小球”好像“记得”
自己起始的高度
问题:这里守恒量是什么?
什么是不变的?
会不会是h+v?
×
势能Ep
动能Ek
会不会是Ep+Ek?
猜想:
势能:相互作用的物体凭借其位置而具有的
能量叫做势能。
[概念梳理]
动能:运动的物体所具有的能量叫动能。
在A斜面上:a=gsinα
因此小球下落到任意高度都满足
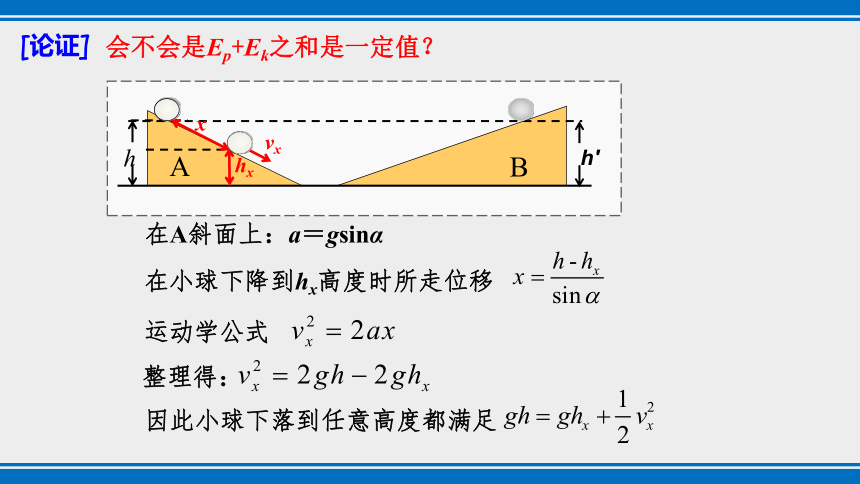
[论证]
会不会是Ep+Ek之和是一定值?
A
B
h
h′
hx
x
vx
在小球下降到hx高度时所走位移
运动学公式
整理得:
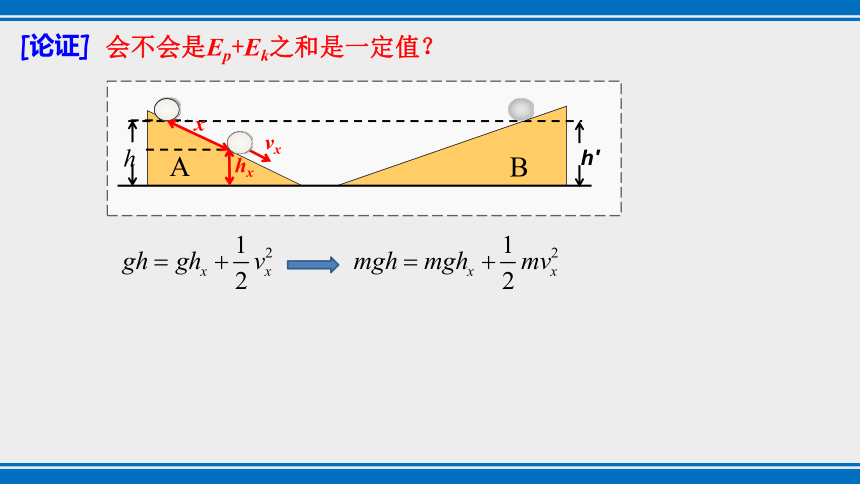
[论证]
会不会是Ep+Ek之和是一定值?
A
B
h
h′
hx
x
vx
伽利略的理想斜面实验
[案例五]
A
B
h
h
下滚过程 上滚过程
现象:“小球”好像“记得”
自己起始的高度
问题:这里守恒量是什么?
会不会是h+v?
×
势能Ep
动能Ek
会不会是Ep+Ek?
结论:
√
机械能E
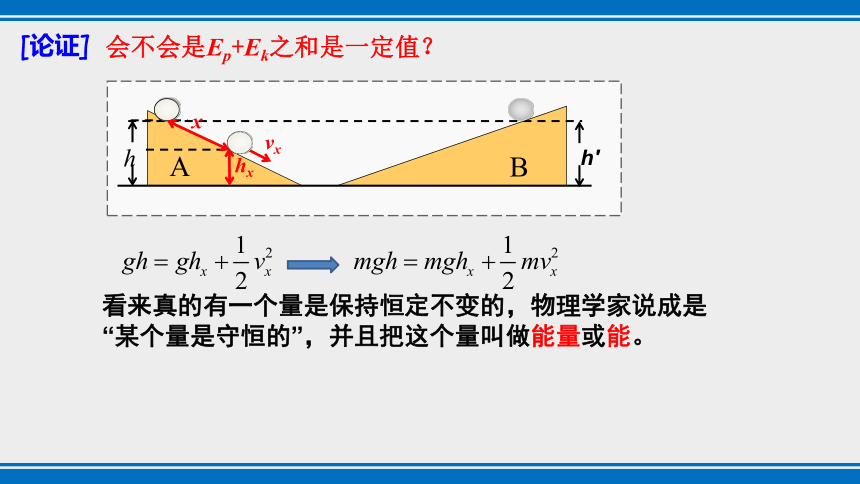
[论证]
会不会是Ep+Ek之和是一定值?
A
B
h
h′
hx
x
vx
看来真的有一个量是保持恒定不变的,物理学家说成是“某个量是守恒的”,并且把这个量叫做能量或能。
有一个事实,如果你愿意,也可以说一条定律,支配着至今所知的一切自然现象……这条定律称做能量守恒定律。它指出某一个量,我们把它称为能量,在自然界经历的多种多样的变化中它不变化。那是一个最抽象的概念……
——费恩曼
(1918-1988美国)
美籍犹太裔物理学家,加州理工学院物理学教授,1965年诺贝尔物理奖得主
费恩曼
[延伸链接]
永动机
人类曾经想设计出永远不需能量输入,却能一直运动着的“永动机”!为此付出了不懈努力!
人类曾经发现类似的“能量不守恒”的现象!
经过研究,结果往往会发现新的能量存在方式!
[延伸链接]
各种各样形式的能
[案例六]
行星运动
[案例七]
单摆
[案例六]
单摆
[案例七]
单摆
[案例八]
滚摆
[案例八]
滚摆
[案例九]
弹簧振子
[案例九]
弹簧振子
有一个事实,如果你愿意,也可以说一条定律,支配着至今所知的一切自然现象……这条定律称做能量守恒定律。它指出某一个量,我们把它称为能量,在自然界经历的多种多样的变化中它不变化。那是一个最抽象的概念……
——费恩曼
(1918-1988美国)
美籍犹太裔物理学家,加州理工学院物理学教授,1965年诺贝尔物理奖得主
费恩曼
“能量”是牛顿没有留给我们的少数力学概念之一,究其原因是能量及其守恒的思想与牛顿的力学研究思路有所不同,能量及其守恒的思想从更抽象层次上反映了物质运动和相互作用的本质。
[反思总结]
追寻守恒量是科学研究的重要思想和方法。
思想和方法则是我们物理学习和研究的精髓和灵魂!
[反思总结]
如果知识的背后没有方法,知识只能是一种沉重的负担;
如果方法的背后没有思想,方法只不过是笨拙的工具。
[反思总结]
[趣味链接]
圆盘为什么会自动往上走?能量不守恒了吗?
谢
谢
聆
听
第1节 追寻守恒量——能量
找棋子
放学后,两个小孩在家中下象棋。下完棋后,当他们收拾象棋时,忽然发现少了3颗棋子,他们找啊找,发现门后有1颗,墙角有1颗,但还是少1颗。他们不放弃,继续寻找,终于在地毯下找到了最后1颗棋子。
问题:支撑两个小孩能够坚持找到最后1颗棋子的信念是什么?
棋子的数量守恒
[案例一]
查水表
自来水公司抄表员最近发现,某小区一单元楼的自来水管道的总表读数和各住户家中分表读数总和不一致。对于这个问题,你有什么想法?
问题:支撑你们有这些想法的依据是什么?
水的体积守恒
[案例二]
沙漏
装有沙子的封闭沙漏,细砂从A中流入B中。A、B中沙子的总质量如何变化?
问题:支撑你们有这种想法的依据是什么?
沙漏中沙子的质量守恒
A
B
[案例三]
化学反应方程式
Fe+2Fe3+= 3Fe2+
问题:配平化学方程式的依据是什么?
原子数守恒、电荷守恒
[案例四]
物理学的任务是发现普遍的自然规律。因为这样的规律的最简单的形式之一表现为某种物理量的不变性,所以对于守恒量的寻求不仅是合理的,而且也是极为重要的研究方向。
——劳厄
(1879-1960德国)
物理学家,1912年发现晶体的X射线衍射现象,并因此获得诺贝尔物理学奖
伽利略的理想斜面实验
[案例五]
A
B
h
h
下滚过程 上滚过程
高 度h
速 度v
此消彼长
现象:“小球”好像“记得”
自己起始的高度
问题:这里守恒量是什么?
什么是不变的?
会不会是h+v?
×
势能Ep
动能Ek
会不会是Ep+Ek?
猜想:
势能:相互作用的物体凭借其位置而具有的
能量叫做势能。
[概念梳理]
动能:运动的物体所具有的能量叫动能。
在A斜面上:a=gsinα
因此小球下落到任意高度都满足
[论证]
会不会是Ep+Ek之和是一定值?
A
B
h
h′
hx
x
vx
在小球下降到hx高度时所走位移
运动学公式
整理得:
[论证]
会不会是Ep+Ek之和是一定值?
A
B
h
h′
hx
x
vx
伽利略的理想斜面实验
[案例五]
A
B
h
h
下滚过程 上滚过程
现象:“小球”好像“记得”
自己起始的高度
问题:这里守恒量是什么?
会不会是h+v?
×
势能Ep
动能Ek
会不会是Ep+Ek?
结论:
√
机械能E
[论证]
会不会是Ep+Ek之和是一定值?
A
B
h
h′
hx
x
vx
看来真的有一个量是保持恒定不变的,物理学家说成是“某个量是守恒的”,并且把这个量叫做能量或能。
有一个事实,如果你愿意,也可以说一条定律,支配着至今所知的一切自然现象……这条定律称做能量守恒定律。它指出某一个量,我们把它称为能量,在自然界经历的多种多样的变化中它不变化。那是一个最抽象的概念……
——费恩曼
(1918-1988美国)
美籍犹太裔物理学家,加州理工学院物理学教授,1965年诺贝尔物理奖得主
费恩曼
[延伸链接]
永动机
人类曾经想设计出永远不需能量输入,却能一直运动着的“永动机”!为此付出了不懈努力!
人类曾经发现类似的“能量不守恒”的现象!
经过研究,结果往往会发现新的能量存在方式!
[延伸链接]
各种各样形式的能
[案例六]
行星运动
[案例七]
单摆
[案例六]
单摆
[案例七]
单摆
[案例八]
滚摆
[案例八]
滚摆
[案例九]
弹簧振子
[案例九]
弹簧振子
有一个事实,如果你愿意,也可以说一条定律,支配着至今所知的一切自然现象……这条定律称做能量守恒定律。它指出某一个量,我们把它称为能量,在自然界经历的多种多样的变化中它不变化。那是一个最抽象的概念……
——费恩曼
(1918-1988美国)
美籍犹太裔物理学家,加州理工学院物理学教授,1965年诺贝尔物理奖得主
费恩曼
“能量”是牛顿没有留给我们的少数力学概念之一,究其原因是能量及其守恒的思想与牛顿的力学研究思路有所不同,能量及其守恒的思想从更抽象层次上反映了物质运动和相互作用的本质。
[反思总结]
追寻守恒量是科学研究的重要思想和方法。
思想和方法则是我们物理学习和研究的精髓和灵魂!
[反思总结]
如果知识的背后没有方法,知识只能是一种沉重的负担;
如果方法的背后没有思想,方法只不过是笨拙的工具。
[反思总结]
[趣味链接]
圆盘为什么会自动往上走?能量不守恒了吗?
谢
谢
聆
听
