人教版初中数学七年级下册5.2.1《平行线(定义、平行公理及推论)》课件(共34张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册5.2.1《平行线(定义、平行公理及推论)》课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-29 00:00:00 | ||
图片预览






文档简介
(共34张PPT)
初一年级 数学
平行线的概念与平行公理及其推论
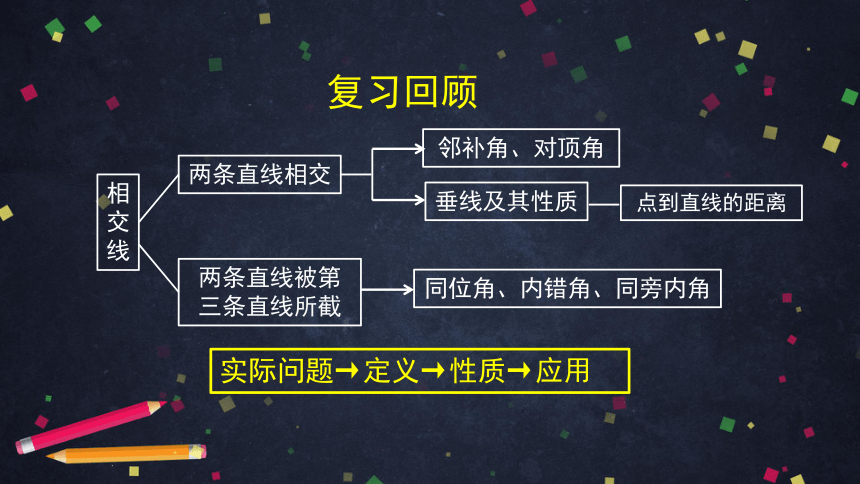
相交
线
两条直线相交
邻补角、对顶角
垂线及其性质
点到直线的距离
两条直线被第三条直线所截
同位角、内错角、同旁内角
实际问题→定义→性质→应用
复习回顾
生活中的相交线与平行线
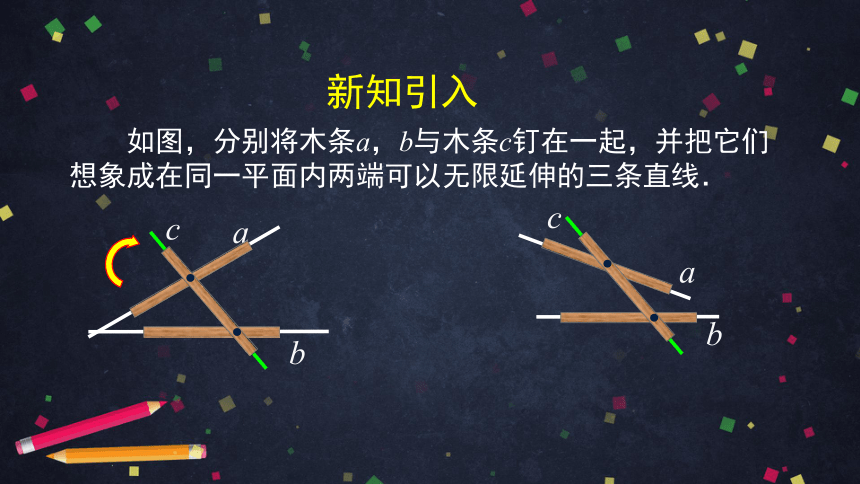
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
a
b
c
a
a
a
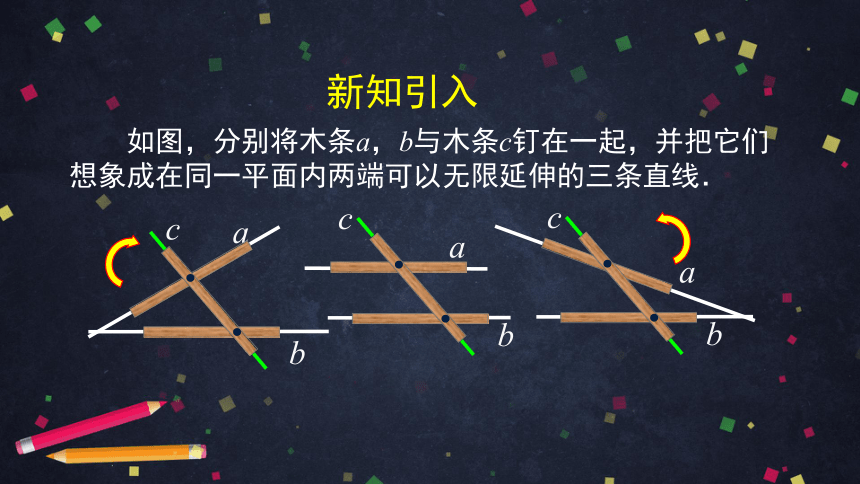
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
b
c
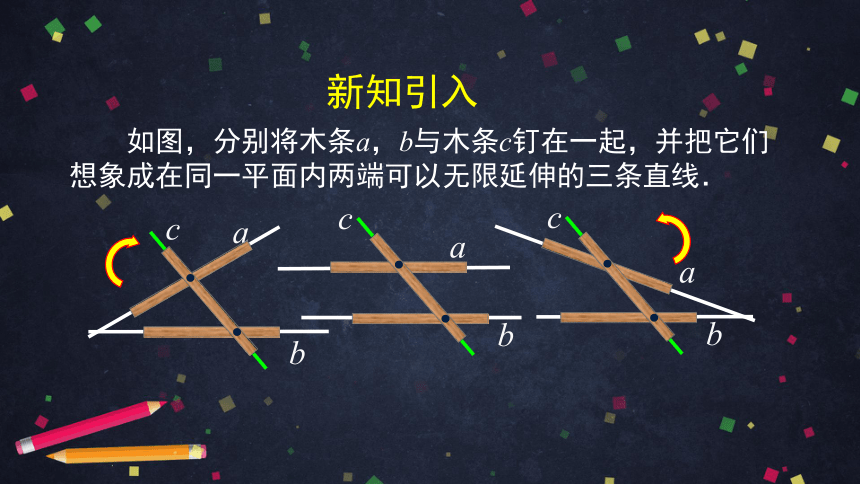
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
b
c
b
c
a
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
b
c
b
c
a
b
c
a
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
b
c
b
c
a
b
c
a
新知引入
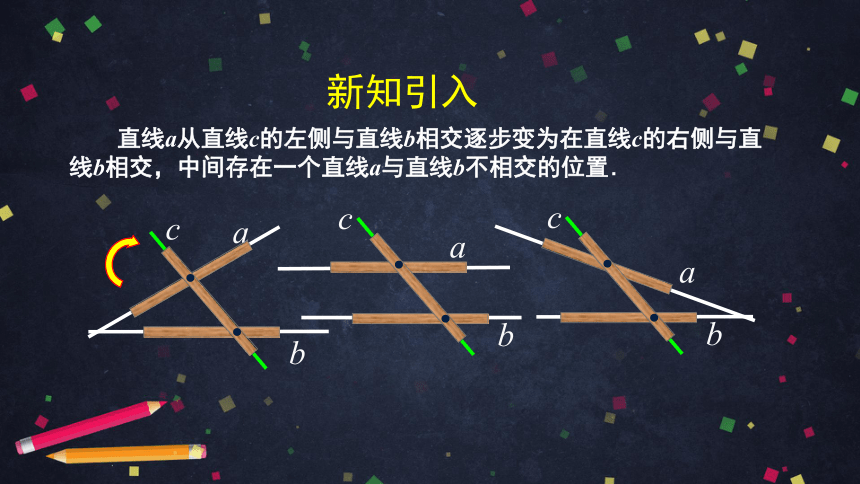
直线a从直线c的左侧与直线b相交逐步变为在直线c的右侧与直线b相交,中间存在一个直线a与直线b不相交的位置.
a
b
c
b
c
a
b
c
a
直线a与b不相交,
则我们说a与b互相平行.
记作a∥b.
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
新知引入
a
b
c
平行线在生活中很常见.
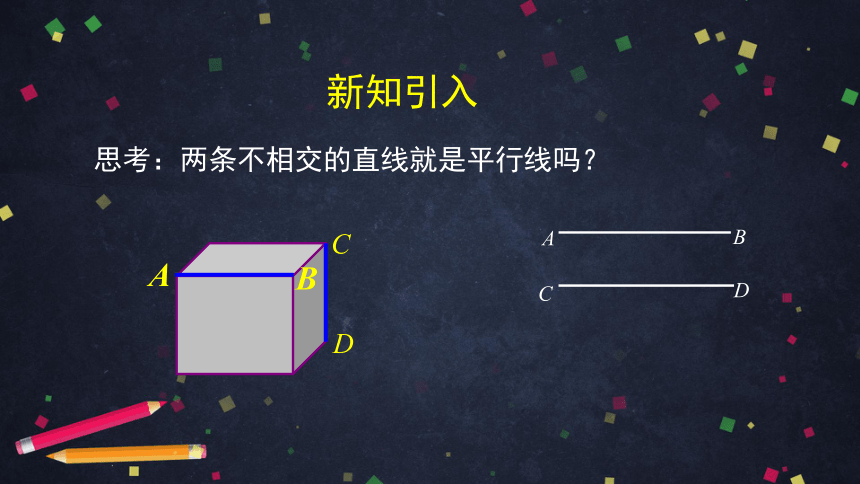
思考:两条不相交的直线就是平行线吗?
A
B
C
D
新知引入
A
B
C
D
平行线的定义
不相交的两条直线叫做平行线.
在同一平面内,
C
D
A
B
A
B
C
D
平行线的定义
不相交的两条直线叫做平行线.
在同一平面内,
符号表示:
如图,直线AB与直线CD平行,
记作“AB∥CD”,
读作“AB平行于CD”.
A
B
C
D
思考:在同一平面内任意画两条不重合的直线,它们的位置关系有几种情况?
平行线的定义
平行
相交
a
b
a
b
a
b
在同一平面内,
不重合的两条直线只有两种位置关系:
相交和平行.
思考1:如图,转动木条a的过程中,有几个位置使得直线a与b平行?
新知探究
a
a
b
c
a
a
a
b
c
a
P
如图,转动木条a的过程中,有几个位置使得直线a与b平行?
新知探究
b
P
过直线b外一点P能画几条直线与已知直线b平行?
b
c
a
b
P
新知探究
思考2:如图,过点P画直线b的平行线,能画出几条?
a
b
P
新知探究
思考2:如图,过点P画直线b的平行线,能画出几条?
a
再过点Q画直线b的平行线,能画出几条?
Q
c
b
P
a
Q
c
新知探究
经过直线外一点,有且只有一条直线与这条直线平行.
基本事实
(平行公理)
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
存在
唯一
新知探究
经过直线外一点,有且只有一条直线与这条直线平行.
基本事实
(平行公理)
猜想: 如果两条直线都与第三条直线平行,那么这两条直线互相平行.
b
P
a
Q
c
b
a
c
新知探究
如果a∥b,c∥b,那么a∥c.
P
设交点为P,
那么过点P就有两条直线a和c都与直线b平行,而根据前面的平行公理,这是不可能的,因此a∥c.
假设a与c不平行,
那么a与c相交,
b
a
c
平行公理及其推论
经过直线外一点,有且只有一条直线与这条直线平行.
基本事实
(平行公理)
推论: 如果两条直线都与第三条直线平行,那么这两条直线互相平行.
b
a
c
平行公理及其推论
推论: 如果两条直线都与第三条直线平行,那么这两条直线互相平行.
如果a∥b,c∥b,那么a∥c.
a∥b,c∥b
a∥c
因为a∥b,c∥b,
所以a∥c.
b
a
c
平行公理及其推论
经过直线外一点,有且只有一条直线与这条直线平行.
基本事实
(平行公理)
推论: 如果两条直线都与第三条直线平行,那么这两条直线互相平行.
如果a∥b,c∥b,那么a∥c.
唯一性
传递性
P
典例分析
例1 如图,点P 是∠AOB内一点,请过点P画PC∥OA交OB于点C,画PD∥OB交OA于点D.
过点P画PC∥OA交OB于点C
P
P
过点P画PD∥OB交OA于点D
先画平行,再找交点
典例分析
例1 如图,点P 是∠AOB内一点,请过点P画PC∥OA交OB于点C,画PD∥OB交OA于点D.
P
O
A
B
C
D
直线AB,CD是相交直线,点P 是直线AB,CD 外的一点,直线EF经过点P 且与直线AB平行,
与直线CD相交于点E .
例2 读下列语句,并画出图形:
典例分析
例2 读下列语句,并画出图形:
典例分析
①直线AB,CD是相交直线;
②点P是直线AB,CD外的一点;
③直线EF:经过点P,与直线AB平行,与直线CD相交于点E.
直线AB,CD是相交直线,点P是直线AB,CD外的一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E.
例2 读下列语句,并画出图形:
A
D
C
E
F
B
P
典例分析
①直线AB,CD是相交直线;
②点P是直线AB,CD外的一点;
③直线EF:经过点P,与直线AB平行,与直线CD相交于点E.
解题小结
几何画图
文字语言
符号语言
图形语言
几何识图
平行
相交
a
b
a
b
a
b
平行线的定义
平行线的画法
平行公理及推论
a
b
c
同一平面内,两条直线
课堂小结
课后作业
观察如图所示的长方体,用符号表示下列两棱的位置关系:A1B1 AB,AA1 AB,A1D1 C1D1,AD BC.
你能在房间里找到这些位置关系的实例吗?与同学们讨论一下.
同学们再见!
初一年级 数学
平行线的概念与平行公理及其推论
相交
线
两条直线相交
邻补角、对顶角
垂线及其性质
点到直线的距离
两条直线被第三条直线所截
同位角、内错角、同旁内角
实际问题→定义→性质→应用
复习回顾
生活中的相交线与平行线
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
a
b
c
a
a
a
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
b
c
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
b
c
b
c
a
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
b
c
b
c
a
b
c
a
新知引入
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
a
b
c
b
c
a
b
c
a
新知引入
直线a从直线c的左侧与直线b相交逐步变为在直线c的右侧与直线b相交,中间存在一个直线a与直线b不相交的位置.
a
b
c
b
c
a
b
c
a
直线a与b不相交,
则我们说a与b互相平行.
记作a∥b.
如图,分别将木条a,b与木条c钉在一起,并把它们想象成在同一平面内两端可以无限延伸的三条直线.
新知引入
a
b
c
平行线在生活中很常见.
思考:两条不相交的直线就是平行线吗?
A
B
C
D
新知引入
A
B
C
D
平行线的定义
不相交的两条直线叫做平行线.
在同一平面内,
C
D
A
B
A
B
C
D
平行线的定义
不相交的两条直线叫做平行线.
在同一平面内,
符号表示:
如图,直线AB与直线CD平行,
记作“AB∥CD”,
读作“AB平行于CD”.
A
B
C
D
思考:在同一平面内任意画两条不重合的直线,它们的位置关系有几种情况?
平行线的定义
平行
相交
a
b
a
b
a
b
在同一平面内,
不重合的两条直线只有两种位置关系:
相交和平行.
思考1:如图,转动木条a的过程中,有几个位置使得直线a与b平行?
新知探究
a
a
b
c
a
a
a
b
c
a
P
如图,转动木条a的过程中,有几个位置使得直线a与b平行?
新知探究
b
P
过直线b外一点P能画几条直线与已知直线b平行?
b
c
a
b
P
新知探究
思考2:如图,过点P画直线b的平行线,能画出几条?
a
b
P
新知探究
思考2:如图,过点P画直线b的平行线,能画出几条?
a
再过点Q画直线b的平行线,能画出几条?
Q
c
b
P
a
Q
c
新知探究
经过直线外一点,有且只有一条直线与这条直线平行.
基本事实
(平行公理)
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
存在
唯一
新知探究
经过直线外一点,有且只有一条直线与这条直线平行.
基本事实
(平行公理)
猜想: 如果两条直线都与第三条直线平行,那么这两条直线互相平行.
b
P
a
Q
c
b
a
c
新知探究
如果a∥b,c∥b,那么a∥c.
P
设交点为P,
那么过点P就有两条直线a和c都与直线b平行,而根据前面的平行公理,这是不可能的,因此a∥c.
假设a与c不平行,
那么a与c相交,
b
a
c
平行公理及其推论
经过直线外一点,有且只有一条直线与这条直线平行.
基本事实
(平行公理)
推论: 如果两条直线都与第三条直线平行,那么这两条直线互相平行.
b
a
c
平行公理及其推论
推论: 如果两条直线都与第三条直线平行,那么这两条直线互相平行.
如果a∥b,c∥b,那么a∥c.
a∥b,c∥b
a∥c
因为a∥b,c∥b,
所以a∥c.
b
a
c
平行公理及其推论
经过直线外一点,有且只有一条直线与这条直线平行.
基本事实
(平行公理)
推论: 如果两条直线都与第三条直线平行,那么这两条直线互相平行.
如果a∥b,c∥b,那么a∥c.
唯一性
传递性
P
典例分析
例1 如图,点P 是∠AOB内一点,请过点P画PC∥OA交OB于点C,画PD∥OB交OA于点D.
过点P画PC∥OA交OB于点C
P
P
过点P画PD∥OB交OA于点D
先画平行,再找交点
典例分析
例1 如图,点P 是∠AOB内一点,请过点P画PC∥OA交OB于点C,画PD∥OB交OA于点D.
P
O
A
B
C
D
直线AB,CD是相交直线,点P 是直线AB,CD 外的一点,直线EF经过点P 且与直线AB平行,
与直线CD相交于点E .
例2 读下列语句,并画出图形:
典例分析
例2 读下列语句,并画出图形:
典例分析
①直线AB,CD是相交直线;
②点P是直线AB,CD外的一点;
③直线EF:经过点P,与直线AB平行,与直线CD相交于点E.
直线AB,CD是相交直线,点P是直线AB,CD外的一点,直线EF经过点P且与直线AB平行,与直线CD相交于点E.
例2 读下列语句,并画出图形:
A
D
C
E
F
B
P
典例分析
①直线AB,CD是相交直线;
②点P是直线AB,CD外的一点;
③直线EF:经过点P,与直线AB平行,与直线CD相交于点E.
解题小结
几何画图
文字语言
符号语言
图形语言
几何识图
平行
相交
a
b
a
b
a
b
平行线的定义
平行线的画法
平行公理及推论
a
b
c
同一平面内,两条直线
课堂小结
课后作业
观察如图所示的长方体,用符号表示下列两棱的位置关系:A1B1 AB,AA1 AB,A1D1 C1D1,AD BC.
你能在房间里找到这些位置关系的实例吗?与同学们讨论一下.
同学们再见!
