北京课改版数学八下14.2《函数的表示法》课件 (第一课时 共40张PPT)
文档属性
| 名称 | 北京课改版数学八下14.2《函数的表示法》课件 (第一课时 共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-29 20:44:38 | ||
图片预览











文档简介
(共40张PPT)
初二年级 数学
函数的表示法(第一课时)
一、知识要点回顾:
1.函数定义:
一般地,在一个变化过程中,有两个变量 x 和 y,对于变量 x 的每一个值,变量 y 都有唯一确定的值和它对应,
我们就把 x 称为自变量,
y 称为因变量,y 是 x 的函数.
2.函数自变量的取值范围:
一般地,研究函数时应考虑函数的自变量的取
x≠0
值范围.
x≥0
x可取任意实数
已知:等腰三角形的周长为20cm,若设底边长为 ycm,腰长xcm,则y与x之间的关系可表示为____
.
自变量x的取值范围是 .
;
由等腰三角形的周长是20cm,可得三边之和为20cm
分析:
即 y+2x=20,
变形可得:y=20-2x.
分析:我们再来看自变量的取值范围,对于变量
x和y它们代表的是三角形的边长,所以应该满足
的前提条件是三边长满足三角形的三边关系,故有,
x-x< y < x+x,
即 0< 20-2x <2x.
5< x <10.
x>0, y>0;
解得,
又因为围成三角形
即x>0,20-2x>0 ;
已知:等腰三角形的周长为20cm,若设底边长为 ycm,腰长为xcm,则y与x之间的关系可表示为:
自变量x的取值范围是 .
y=20-2x ;
5< x <10
自变量 因变量
s= 80t
y= 3x2-2x+4
t
s
x
y
x
y
这些表示函数的式子
有什么共同的特征?
s= 80t,y= 3x2-2x+4,
像这样用含有表示自变量的字母的代数式表示因变
二、函数的表达式
用这种表示函数关系的方法称为解析法.
.
量的式子叫做函数的表达式.
例如s= 80t
利用函数的表达式可以由函数的任意一个自变量的 值,求出相应的函数的值(简称函数值),也可以
t
s
1
80
2
…
…
…
…
160
3
240
由某一个确定的函数值求出相应的自变量的值.
400
5
例1: 已知两个函数的表达式分别为
y=2x-5 和
(1)当x=﹣4时,分别求出这两个函数的函数值;
三、例题解析
.
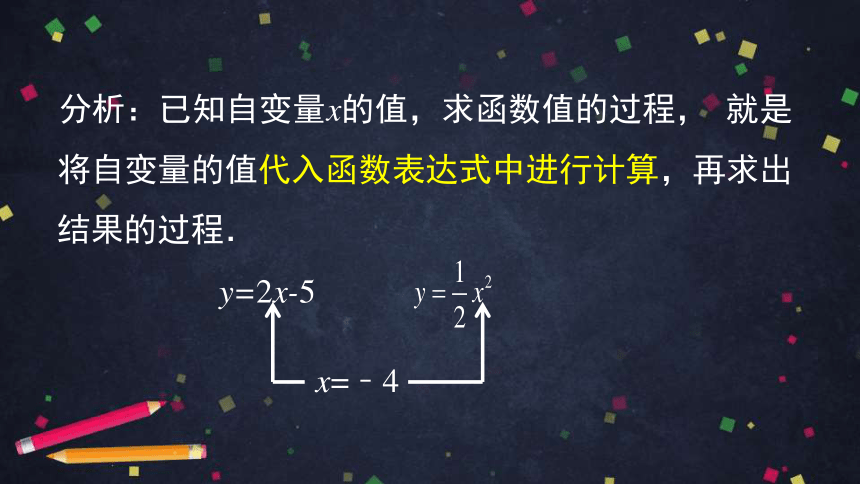
分析:已知自变量x的值,求函数值的过程, 就是将自变量的值代入函数表达式中进行计算,再求出
结果的过程.
y=2x-5
x=﹣4
(1)把 分别代入这两个函数表达式,得
y=2x-5
∴当x=﹣4时,函数y=2x-5的函数值为-13,函数
的函数值为8.
解:
例1: 已知两个函数的表达式分别为
y=2x-5 和
(2)当这两个函数的函数值都为18时,自变量x分
别取什么值?
.
若已知函数的函数值 y,将其代入函数表达式后会得到关于自变量x的方程,解这个方程就可以
分析:
得到自变量x的取值.
y=2x-5
y=18
解:(2)把函数值y=18代入函数的表达式
18=2x-5,
解这个方程,得
2x=23
一元一次方程
转化
y=2x-5,
得
.
.
.
把函数值y=18代入函数的表达式 ,得
于是,得
x2=36
一元二次方程
转化
或
.
.
.
因为x是36的平方根,所以
y=2x﹣5
的自变量x的值为
∴当这两个函数的函数值都为18时,函数
,函数
为 .
的自变量x的值
小结:
1.若已知函数的自变量取值,将其代入函数表达式,
就可以得到函数值;
x=﹣4
y=2x-5
小结:
2.若已知函数的函数值,则可以通过解方程来求出
对应的自变量的值.
y=2x-5
y=18
例2:
一辆汽车的油箱中现有 ,
那么油箱中的油量y (单位:升)随行驶里程
汽油50升
不再加
x(单位:千米)的增加而减少,平均耗油量为
如果
油,
0.1升/千米.
(1)写出表示y与x的函数关系的式子;
分析:
平均耗油量为0.1升/千米,也就是说每行驶1千米,耗油量为0.1升.所以行驶 x千米时,耗油
油箱中的油量=现有油量-所耗油量.
量为0.1x 升.
解:
(1)行驶里程x(单位:千米)是自变量,油箱
中的油量y(单位:升)是x的函数,它们的关系式
为:
.
例2:
一辆汽车的油箱中现有 ,
那么油箱中的油量y (单位:升)随行驶里程
汽油50升
不再加
x(单位:千米)的增加而减少,平均耗油量为
如果
油
0.1升/千米.
(2)求这个函数自变量的取值范围;
(2)仅从式子 看,x可以取任
分析:
意实数,但是考虑到x代表的实际意义为行驶里程,
所以x不能取负数.
即 ;
又因为行驶中的耗油量
油箱中现有汽油50升,
即
为0.1x,它不能超过
所以,这个函数自变量的取值范围是
解:
(2)由题意得,
解得,
.
.
例2:
一辆汽车的油箱中现有 ,
那么油箱中的油量y (单位:升)随行驶里程
汽油50升
不再加
x(单位:千米)的增加而减少,平均耗油量为
如果
油
0.1升/千米.
(3)汽车行驶200千米时,油箱中还有多少汽油?
(3)
解:
将x=200代入 ,得
所以,汽车行驶200千米,油箱中还有
30升汽油.
小结:
1.可以用函数的表达式来表示某些实际问题中的
两个变量间的关系.
例如:
2.实际问题的背景会对函数自变量的取值范围产生
影响,需要考虑清楚.
例如:
小结:
3.若对于自变量的不同取值,函数值有相同的对应
规律,则可以考虑用解析法来表示两个变量间的函
数关系.
例如:y= 3x2-2x+4
例3:我们知道,海拔高度每上升1km,温度下降
(1)写出y与x的函数表达式;
6℃.某时刻,地面温度20℃,设距离地面x(km)
处的温度为y(℃).
分析:海拔高度每上升1km,温度下降6 ℃.高度
上升xkm,温度应该下降6x ℃.
所以,
地面温度-
x千米高度的温度=
下降温度
解:
(1)
( x ≥ 0 )
例3:我们知道,海拔高度每上升1km,温度下降
6℃.某时刻,地面温度20℃,设距离地面x(km)
处的温度为y(℃).
(2)此时有一架飞机飞过上空,若机舱内仪表显示飞机外面的温度为-34 ℃,则飞机飞行的高度为多
少?
分析:此刻,飞机外面的温度为-34 ℃,也就是上
面表达式中y的值,所以,将y=-34代入函数表达式,
即可求出自变量x的值.
解:
(2)由题意,得y=-34,把y=-34代入
中,得
答:飞机飞行的高度为9千米.
解这个方程,得
.
四、课堂小结:
1.函数的表达式
用含有表示自变量的字母的代数式表示因变量的式
子叫做函数的表达式.
四、课堂小结:
2.应用函数表达式可以由自变量的每一个值,计算出相对应的函数的值,也可以由某一个确定的函数
值求出相应的自变量的值.
(转化思想)
四、课堂小结:
解析法具有形式简单,关系明确的特点.
叫做解析法.
3.函数的表示法——解析法.
用表达式来表示两个变量之间的函数关系的方法就
作业 :
1.已知城市轻轨列车的平均速度约是1330m/min.
廖欣同学每天上学时,须先步行850m到达车站.
当他上车后,离家的总路程s是他上车后的时间t的
函数吗?如果是,请写出这个函数关系.
2.一种可推拉的长方形塑钢窗,长862mm,打开
时的最大宽度475mm.若设打开的宽度为xmm .
(1)写出打开部分的面积s(mm2)与打开的宽度
x(mm)的函数表达式;
(2)写出自变量x的取值范围.
作业 :
初二年级 数学
函数的表示法(第一课时)
一、知识要点回顾:
1.函数定义:
一般地,在一个变化过程中,有两个变量 x 和 y,对于变量 x 的每一个值,变量 y 都有唯一确定的值和它对应,
我们就把 x 称为自变量,
y 称为因变量,y 是 x 的函数.
2.函数自变量的取值范围:
一般地,研究函数时应考虑函数的自变量的取
x≠0
值范围.
x≥0
x可取任意实数
已知:等腰三角形的周长为20cm,若设底边长为 ycm,腰长xcm,则y与x之间的关系可表示为____
.
自变量x的取值范围是 .
;
由等腰三角形的周长是20cm,可得三边之和为20cm
分析:
即 y+2x=20,
变形可得:y=20-2x.
分析:我们再来看自变量的取值范围,对于变量
x和y它们代表的是三角形的边长,所以应该满足
的前提条件是三边长满足三角形的三边关系,故有,
x-x< y < x+x,
即 0< 20-2x <2x.
5< x <10.
x>0, y>0;
解得,
又因为围成三角形
即x>0,20-2x>0 ;
已知:等腰三角形的周长为20cm,若设底边长为 ycm,腰长为xcm,则y与x之间的关系可表示为:
自变量x的取值范围是 .
y=20-2x ;
5< x <10
自变量 因变量
s= 80t
y= 3x2-2x+4
t
s
x
y
x
y
这些表示函数的式子
有什么共同的特征?
s= 80t,y= 3x2-2x+4,
像这样用含有表示自变量的字母的代数式表示因变
二、函数的表达式
用这种表示函数关系的方法称为解析法.
.
量的式子叫做函数的表达式.
例如s= 80t
利用函数的表达式可以由函数的任意一个自变量的 值,求出相应的函数的值(简称函数值),也可以
t
s
1
80
2
…
…
…
…
160
3
240
由某一个确定的函数值求出相应的自变量的值.
400
5
例1: 已知两个函数的表达式分别为
y=2x-5 和
(1)当x=﹣4时,分别求出这两个函数的函数值;
三、例题解析
.
分析:已知自变量x的值,求函数值的过程, 就是将自变量的值代入函数表达式中进行计算,再求出
结果的过程.
y=2x-5
x=﹣4
(1)把 分别代入这两个函数表达式,得
y=2x-5
∴当x=﹣4时,函数y=2x-5的函数值为-13,函数
的函数值为8.
解:
例1: 已知两个函数的表达式分别为
y=2x-5 和
(2)当这两个函数的函数值都为18时,自变量x分
别取什么值?
.
若已知函数的函数值 y,将其代入函数表达式后会得到关于自变量x的方程,解这个方程就可以
分析:
得到自变量x的取值.
y=2x-5
y=18
解:(2)把函数值y=18代入函数的表达式
18=2x-5,
解这个方程,得
2x=23
一元一次方程
转化
y=2x-5,
得
.
.
.
把函数值y=18代入函数的表达式 ,得
于是,得
x2=36
一元二次方程
转化
或
.
.
.
因为x是36的平方根,所以
y=2x﹣5
的自变量x的值为
∴当这两个函数的函数值都为18时,函数
,函数
为 .
的自变量x的值
小结:
1.若已知函数的自变量取值,将其代入函数表达式,
就可以得到函数值;
x=﹣4
y=2x-5
小结:
2.若已知函数的函数值,则可以通过解方程来求出
对应的自变量的值.
y=2x-5
y=18
例2:
一辆汽车的油箱中现有 ,
那么油箱中的油量y (单位:升)随行驶里程
汽油50升
不再加
x(单位:千米)的增加而减少,平均耗油量为
如果
油,
0.1升/千米.
(1)写出表示y与x的函数关系的式子;
分析:
平均耗油量为0.1升/千米,也就是说每行驶1千米,耗油量为0.1升.所以行驶 x千米时,耗油
油箱中的油量=现有油量-所耗油量.
量为0.1x 升.
解:
(1)行驶里程x(单位:千米)是自变量,油箱
中的油量y(单位:升)是x的函数,它们的关系式
为:
.
例2:
一辆汽车的油箱中现有 ,
那么油箱中的油量y (单位:升)随行驶里程
汽油50升
不再加
x(单位:千米)的增加而减少,平均耗油量为
如果
油
0.1升/千米.
(2)求这个函数自变量的取值范围;
(2)仅从式子 看,x可以取任
分析:
意实数,但是考虑到x代表的实际意义为行驶里程,
所以x不能取负数.
即 ;
又因为行驶中的耗油量
油箱中现有汽油50升,
即
为0.1x,它不能超过
所以,这个函数自变量的取值范围是
解:
(2)由题意得,
解得,
.
.
例2:
一辆汽车的油箱中现有 ,
那么油箱中的油量y (单位:升)随行驶里程
汽油50升
不再加
x(单位:千米)的增加而减少,平均耗油量为
如果
油
0.1升/千米.
(3)汽车行驶200千米时,油箱中还有多少汽油?
(3)
解:
将x=200代入 ,得
所以,汽车行驶200千米,油箱中还有
30升汽油.
小结:
1.可以用函数的表达式来表示某些实际问题中的
两个变量间的关系.
例如:
2.实际问题的背景会对函数自变量的取值范围产生
影响,需要考虑清楚.
例如:
小结:
3.若对于自变量的不同取值,函数值有相同的对应
规律,则可以考虑用解析法来表示两个变量间的函
数关系.
例如:y= 3x2-2x+4
例3:我们知道,海拔高度每上升1km,温度下降
(1)写出y与x的函数表达式;
6℃.某时刻,地面温度20℃,设距离地面x(km)
处的温度为y(℃).
分析:海拔高度每上升1km,温度下降6 ℃.高度
上升xkm,温度应该下降6x ℃.
所以,
地面温度-
x千米高度的温度=
下降温度
解:
(1)
( x ≥ 0 )
例3:我们知道,海拔高度每上升1km,温度下降
6℃.某时刻,地面温度20℃,设距离地面x(km)
处的温度为y(℃).
(2)此时有一架飞机飞过上空,若机舱内仪表显示飞机外面的温度为-34 ℃,则飞机飞行的高度为多
少?
分析:此刻,飞机外面的温度为-34 ℃,也就是上
面表达式中y的值,所以,将y=-34代入函数表达式,
即可求出自变量x的值.
解:
(2)由题意,得y=-34,把y=-34代入
中,得
答:飞机飞行的高度为9千米.
解这个方程,得
.
四、课堂小结:
1.函数的表达式
用含有表示自变量的字母的代数式表示因变量的式
子叫做函数的表达式.
四、课堂小结:
2.应用函数表达式可以由自变量的每一个值,计算出相对应的函数的值,也可以由某一个确定的函数
值求出相应的自变量的值.
(转化思想)
四、课堂小结:
解析法具有形式简单,关系明确的特点.
叫做解析法.
3.函数的表示法——解析法.
用表达式来表示两个变量之间的函数关系的方法就
作业 :
1.已知城市轻轨列车的平均速度约是1330m/min.
廖欣同学每天上学时,须先步行850m到达车站.
当他上车后,离家的总路程s是他上车后的时间t的
函数吗?如果是,请写出这个函数关系.
2.一种可推拉的长方形塑钢窗,长862mm,打开
时的最大宽度475mm.若设打开的宽度为xmm .
(1)写出打开部分的面积s(mm2)与打开的宽度
x(mm)的函数表达式;
(2)写出自变量x的取值范围.
作业 :
同课章节目录
