北京课改版数学八年级下册14.2《函数的表示法》(第二课时)课件 (共42张PPT)
文档属性
| 名称 | 北京课改版数学八年级下册14.2《函数的表示法》(第二课时)课件 (共42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-29 20:45:43 | ||
图片预览











文档简介
(共42张PPT)
函数的表示法(第二课时)
八年级下册 数学
知识要点回顾
解析法
S =80t
y =3x2-2x+4
像这样用含有表示自变量的字母的代数式表示因变量的式子叫做函数的表达式.
这种表示函数关系的方法称为解析法.
解析法的特点:
用解析法表示函数关系形式简单,关系明确.
是否所有的函数关系都能用解析法来表示呢?
例1 某城市有一路全程22站的公共汽车,其票价是这样规定的:
1~4站, 1.00元;5~8站, 1.50元;
9~14站,2.00元;15~22站,2.50元.
票价是乘车站数的函数吗?
1~4站, 1.00元;
5~8站, 1.50元;
9~14站, 2 .00元;
15~22站, 2.50元.
6
17
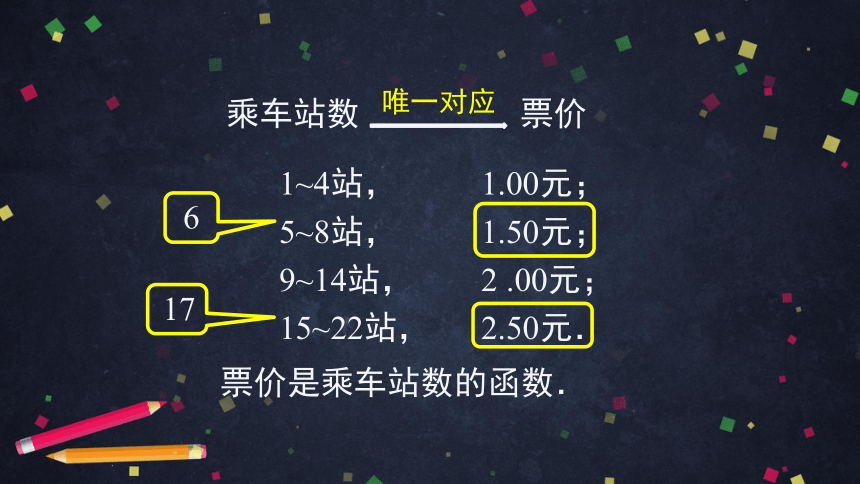
乘车站数
票价
唯一对应
票价是乘车站数的函数.
例1 某城市有一路全程22站的公共汽车,其票价是这样规定的:
1~4站,1.00元;5~8站,1.50元;
9~14站,2.00元;15~22站,2.50元.
怎样表示这个函数呢?
用解析法无法顺利地表示出此函数的关系.
乘车站数
票价/元
1~4
1.00
5~8
1.50
9~14
2.00
15~22
2.50
像这样用列表来表示函数关系的方法称为列表法.
例2 某文具店促销一种圆珠笔,它的单价随购买数量的增加而降低.具体方案如下:
1~5支,每支1.00元;6~10支,每支0.90元;11~20支,每支0.80元;21支及以上,每支0.70元.
顾客购买这种圆珠笔时,付款总额(元)是购买数量(支)的函数吗?
分析:1~5支,每支1.00元;6~10支,每支0.90元;11~20支,每支0.80元;21支及以上,每支0.70元.
购买数量 x(支)
付款总额 y(元)
单价
7
0.90
×
=
6.30
15
0.80
×
=
12.00
唯一对应
付款总额 y(元)是购买的数量 x(支)的函数.
用什么方法表示这个函数关系比较恰当呢?
购买数量x
付款总额y
购买数量x(支) 付款总额y(元)
1 ≤ x ≤ 5
x
6 ≤ x ≤ 10
0.9x
11 ≤ x ≤ 20
0.8x
x ≥ 21
0.7x
将解析法与列表法相结合来表示这个函数.
小结:
1.若对于自变量的不同取值,函数值有相同的对应规律,
则可以考虑用解析法来表示两个变量之间的函数关系.
例如: y=3x2-2x+4
用解析法来表示函数关系,形式简单、明了.
2.若对于自变量的不同取值,函数值有不同的对应规律,
则可以考虑用列表法来表示两个变量间的函数关系.
用列表法来表示函数关系虽然不像解析法那样简洁,但是在表格里两个变量之间的对应关系更加清楚,一目了然.
除了解析法、列表法表示函数关系外,还有其它表示函数关系的方法吗?
例3 洞庭湖地区连日遭受暴雨袭击,导致湖水的水位猛涨,如图是涨水期22日至27日的水位记录.
观察这个图形,你认为在这个问题中,水位是时间的函数吗?
分析:
这几天中的每一时刻,都有唯一确定的水位和它对应.
水位是时间的函数.
观察这个图形,你还能从中获得什么信息?
分析:
可以从以下几个角度来观察图形:
(1)最高水位和最低
水位的情况是怎样的?
(2)水位的上涨和回
落情况是怎样的?
(3)警戒水位开始于
何时?
解:
(1)22日水位最低,为30米,26日水位达到最高,为33.5米;
解:
(2)从22日起,水位开始上涨,26日水位达到最高,从26日起,水位开始
回落;
解:
(3)从24日起,水位开始超过警戒水位,全天水位上涨了1.5米.
用这样的图形表现一个函数关系的变化状态,可以做到直观、简洁和一目了然.
我们把这样的图形叫做这个函数的图象.
用画图象表示函数关系的方法称为图象法.
练习1 骆驼被称为“沙漠之舟”,如图,表示的是48小时内骆驼的体温(℃)随时间而发生变化的图象.
(1)一天中,骆驼的体温的变化范围是什么?它的体温从最低上升到最高需要多长时间?
●
●
35
(2)你能看出第二天8时骆驼的体温与第一天8时有什么关系吗?其它时刻呢?
(3)你还可以获得哪些信息?
●
●
37
●
●
35
练习2 某一天小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,同学们你们能想象出自行车行进路程与行进时间的函数图象吗?
到校后,小明画出了自行车行进路程与行进时间的函数图象,如图所示:
观察图象,你能从中获得哪些信息呢?
A
B
C
分析:
可以从以下几个角度进行观察:
(1)学校与小明家的总路程是多少?
(2)小明从家到学校共用了多长时间?
A
B
C
A
B
C
A
B
C
分析:
(3)你能计算出这一天小明从家到学校的平均速度吗?
(4)图象当中的哪一部分表示的是小明停下来修车?修车用了多长时间?
分析:
(5)小明在修车前和修车后的平均速度各是多少?
(6)你能知道小明平时从家到学校的平均速度是多少吗?
A
B
C
A
B
C
A
B
C
A
B
C
解:
(1)学校与小明家的总路程是4千米.
(2)小明从家到学校共用了0.4小时.
(3)这一天小明从家到学校的平均速度是:
4 ÷0.4=10(千米/时).
A
B
C
A
B
C
解:
(4)图象中线段AB表示的是小明停下来修车,修车用了
0.3-0.2=0.1(小时).
A
B
C
A
B
C
解:
(5)小明在修车前的平均速度是
2 ÷0.2=10(千米/时).
修车后的平均速度是
2 ÷0.1=20(千米/时).
A
B
C
解:(6)根据题意可知,小明这一天和往常一样准时到达了学校,因此这一天所用时间和平时所用的时间是相同的,都是0.4小时,所以平时从家到学校的平均速度也是10千米/时.
A
B
C
A
B
C
小结:
1.函数的三种表示方法:
解析法 列表法 图象法
2.若对于自变量的不同取值,函数值有相同的对应规律,
则可以考虑用解析法来表示两个变量的函数关系.
例如:s =80t y=3x2-2x+4
用解析法来表示函数关系,形式简单,关系明确.
3.若对于自变量的不同取值,函数值有不同的对应规律,
则可以考虑用列表法来表示两个变量间的函数关系.
1~4
1.00
5~8
1.50
9~14
2.00
15~22
2.50
乘车站数
票价/元
用列表法来表示函数关系,两个变量之间的对应关系更加清楚,一目了然.
4.图象法可以直接、形象地把函数关系表示出来.
作业:
1.请你找一个用图象法表示函数的实例,说出你从中获得的信息.
2.一个函数的图象如图所示,根据图象回答下列问题:
(1)写出函数的自变量x的取值范围.
(2)当x的值逐渐变大时,函数值y怎样变化?
(3)求线段AB的长.
(4)求△AOB的面积.
祝同学们
身体健康 学习进步
函数的表示法(第二课时)
八年级下册 数学
知识要点回顾
解析法
S =80t
y =3x2-2x+4
像这样用含有表示自变量的字母的代数式表示因变量的式子叫做函数的表达式.
这种表示函数关系的方法称为解析法.
解析法的特点:
用解析法表示函数关系形式简单,关系明确.
是否所有的函数关系都能用解析法来表示呢?
例1 某城市有一路全程22站的公共汽车,其票价是这样规定的:
1~4站, 1.00元;5~8站, 1.50元;
9~14站,2.00元;15~22站,2.50元.
票价是乘车站数的函数吗?
1~4站, 1.00元;
5~8站, 1.50元;
9~14站, 2 .00元;
15~22站, 2.50元.
6
17
乘车站数
票价
唯一对应
票价是乘车站数的函数.
例1 某城市有一路全程22站的公共汽车,其票价是这样规定的:
1~4站,1.00元;5~8站,1.50元;
9~14站,2.00元;15~22站,2.50元.
怎样表示这个函数呢?
用解析法无法顺利地表示出此函数的关系.
乘车站数
票价/元
1~4
1.00
5~8
1.50
9~14
2.00
15~22
2.50
像这样用列表来表示函数关系的方法称为列表法.
例2 某文具店促销一种圆珠笔,它的单价随购买数量的增加而降低.具体方案如下:
1~5支,每支1.00元;6~10支,每支0.90元;11~20支,每支0.80元;21支及以上,每支0.70元.
顾客购买这种圆珠笔时,付款总额(元)是购买数量(支)的函数吗?
分析:1~5支,每支1.00元;6~10支,每支0.90元;11~20支,每支0.80元;21支及以上,每支0.70元.
购买数量 x(支)
付款总额 y(元)
单价
7
0.90
×
=
6.30
15
0.80
×
=
12.00
唯一对应
付款总额 y(元)是购买的数量 x(支)的函数.
用什么方法表示这个函数关系比较恰当呢?
购买数量x
付款总额y
购买数量x(支) 付款总额y(元)
1 ≤ x ≤ 5
x
6 ≤ x ≤ 10
0.9x
11 ≤ x ≤ 20
0.8x
x ≥ 21
0.7x
将解析法与列表法相结合来表示这个函数.
小结:
1.若对于自变量的不同取值,函数值有相同的对应规律,
则可以考虑用解析法来表示两个变量之间的函数关系.
例如: y=3x2-2x+4
用解析法来表示函数关系,形式简单、明了.
2.若对于自变量的不同取值,函数值有不同的对应规律,
则可以考虑用列表法来表示两个变量间的函数关系.
用列表法来表示函数关系虽然不像解析法那样简洁,但是在表格里两个变量之间的对应关系更加清楚,一目了然.
除了解析法、列表法表示函数关系外,还有其它表示函数关系的方法吗?
例3 洞庭湖地区连日遭受暴雨袭击,导致湖水的水位猛涨,如图是涨水期22日至27日的水位记录.
观察这个图形,你认为在这个问题中,水位是时间的函数吗?
分析:
这几天中的每一时刻,都有唯一确定的水位和它对应.
水位是时间的函数.
观察这个图形,你还能从中获得什么信息?
分析:
可以从以下几个角度来观察图形:
(1)最高水位和最低
水位的情况是怎样的?
(2)水位的上涨和回
落情况是怎样的?
(3)警戒水位开始于
何时?
解:
(1)22日水位最低,为30米,26日水位达到最高,为33.5米;
解:
(2)从22日起,水位开始上涨,26日水位达到最高,从26日起,水位开始
回落;
解:
(3)从24日起,水位开始超过警戒水位,全天水位上涨了1.5米.
用这样的图形表现一个函数关系的变化状态,可以做到直观、简洁和一目了然.
我们把这样的图形叫做这个函数的图象.
用画图象表示函数关系的方法称为图象法.
练习1 骆驼被称为“沙漠之舟”,如图,表示的是48小时内骆驼的体温(℃)随时间而发生变化的图象.
(1)一天中,骆驼的体温的变化范围是什么?它的体温从最低上升到最高需要多长时间?
●
●
35
(2)你能看出第二天8时骆驼的体温与第一天8时有什么关系吗?其它时刻呢?
(3)你还可以获得哪些信息?
●
●
37
●
●
35
练习2 某一天小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,同学们你们能想象出自行车行进路程与行进时间的函数图象吗?
到校后,小明画出了自行车行进路程与行进时间的函数图象,如图所示:
观察图象,你能从中获得哪些信息呢?
A
B
C
分析:
可以从以下几个角度进行观察:
(1)学校与小明家的总路程是多少?
(2)小明从家到学校共用了多长时间?
A
B
C
A
B
C
A
B
C
分析:
(3)你能计算出这一天小明从家到学校的平均速度吗?
(4)图象当中的哪一部分表示的是小明停下来修车?修车用了多长时间?
分析:
(5)小明在修车前和修车后的平均速度各是多少?
(6)你能知道小明平时从家到学校的平均速度是多少吗?
A
B
C
A
B
C
A
B
C
A
B
C
解:
(1)学校与小明家的总路程是4千米.
(2)小明从家到学校共用了0.4小时.
(3)这一天小明从家到学校的平均速度是:
4 ÷0.4=10(千米/时).
A
B
C
A
B
C
解:
(4)图象中线段AB表示的是小明停下来修车,修车用了
0.3-0.2=0.1(小时).
A
B
C
A
B
C
解:
(5)小明在修车前的平均速度是
2 ÷0.2=10(千米/时).
修车后的平均速度是
2 ÷0.1=20(千米/时).
A
B
C
解:(6)根据题意可知,小明这一天和往常一样准时到达了学校,因此这一天所用时间和平时所用的时间是相同的,都是0.4小时,所以平时从家到学校的平均速度也是10千米/时.
A
B
C
A
B
C
小结:
1.函数的三种表示方法:
解析法 列表法 图象法
2.若对于自变量的不同取值,函数值有相同的对应规律,
则可以考虑用解析法来表示两个变量的函数关系.
例如:s =80t y=3x2-2x+4
用解析法来表示函数关系,形式简单,关系明确.
3.若对于自变量的不同取值,函数值有不同的对应规律,
则可以考虑用列表法来表示两个变量间的函数关系.
1~4
1.00
5~8
1.50
9~14
2.00
15~22
2.50
乘车站数
票价/元
用列表法来表示函数关系,两个变量之间的对应关系更加清楚,一目了然.
4.图象法可以直接、形象地把函数关系表示出来.
作业:
1.请你找一个用图象法表示函数的实例,说出你从中获得的信息.
2.一个函数的图象如图所示,根据图象回答下列问题:
(1)写出函数的自变量x的取值范围.
(2)当x的值逐渐变大时,函数值y怎样变化?
(3)求线段AB的长.
(4)求△AOB的面积.
祝同学们
身体健康 学习进步
同课章节目录
