人教版八年级数学下册教学课件:18.2.1 第1课时 矩形的性质(21张)
文档属性
| 名称 | 人教版八年级数学下册教学课件:18.2.1 第1课时 矩形的性质(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 10:36:10 | ||
图片预览



文档简介
课件21张PPT。知识要点1.矩形的性质2.直角三角形斜边上的中线我们生活中充满了矩形这种几何图形,教室里的黑板,门窗,课桌的桌面,信封,明信片等都是矩形的形状,而你是否了解这种几何图形的性质呢?
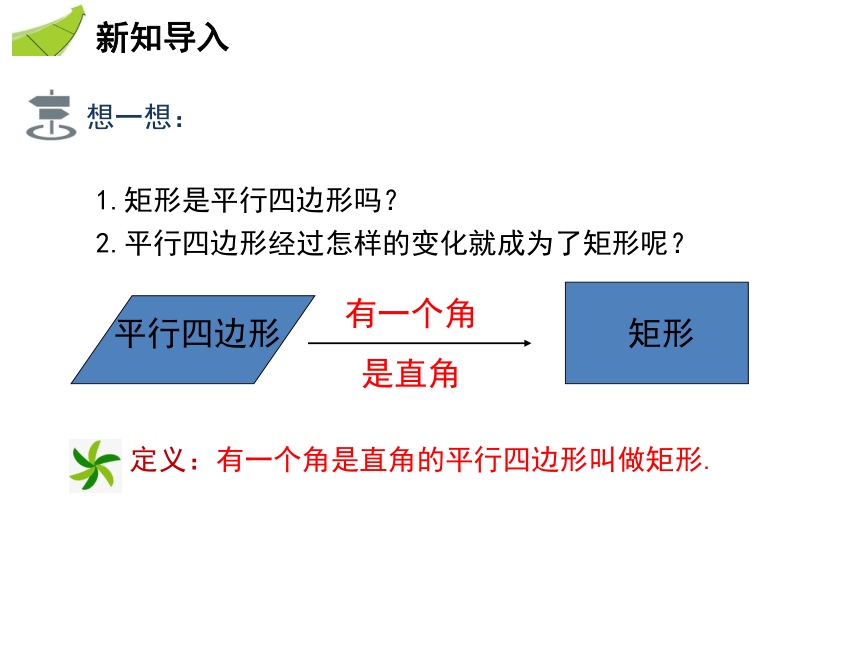
这节课我们一起来学习一下吧!1.矩形是平行四边形吗?2.平行四边形经过怎样的变化就成为了矩形呢?定义:有一个角是直角的平行四边形叫做矩形.
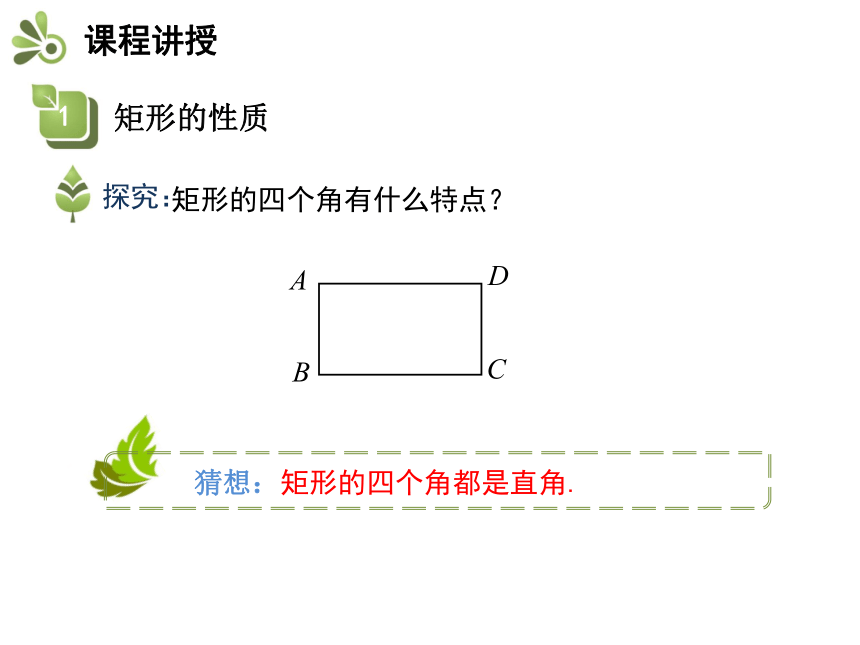
因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?对于矩形,我们仍然从它的边、角和对角线等方面研究 矩形的四个角有什么特点?ABCD证明:∵四边形ABCD是矩形,
∴∠B=∠D,∠C=∠A, AB∥DC.
∴∠B+∠C=180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B=∠C=∠D=∠A =90°.
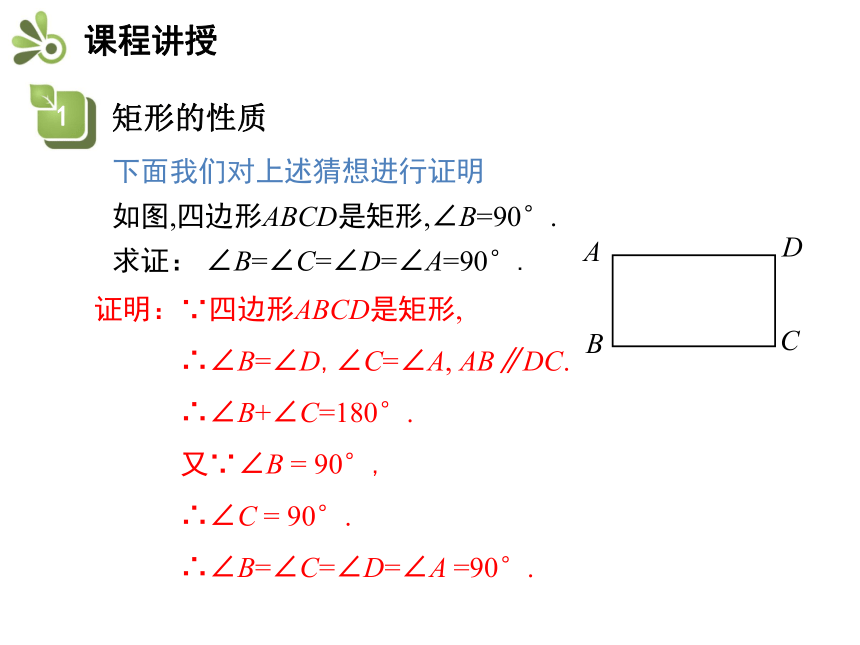
下面我们对上述猜想进行证明
如图,四边形ABCD是矩形,∠B=90°.
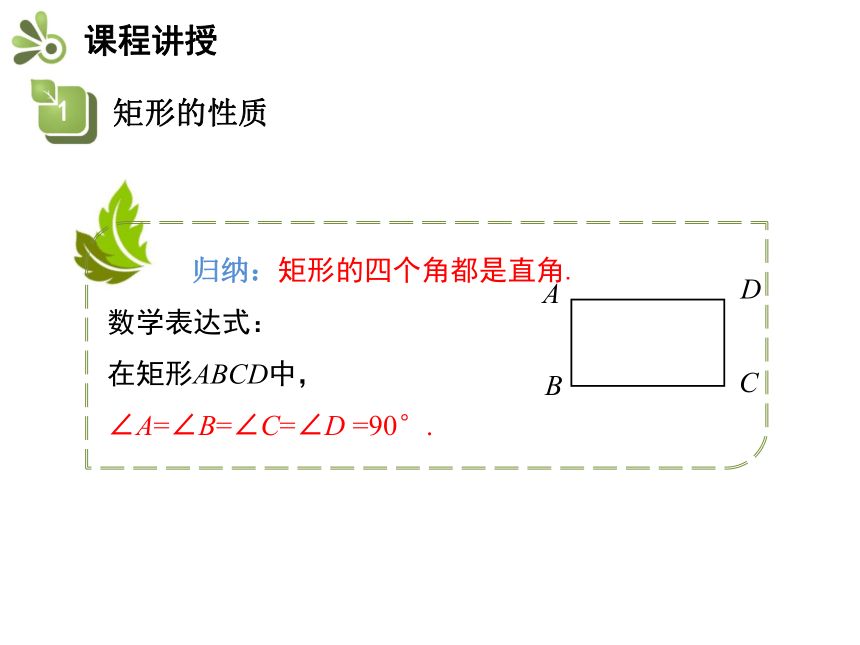
求证: ∠B=∠C=∠D=∠A=90°.ABCD 归纳:矩形的四个角都是直角.
数学表达式:
在矩形ABCD中,
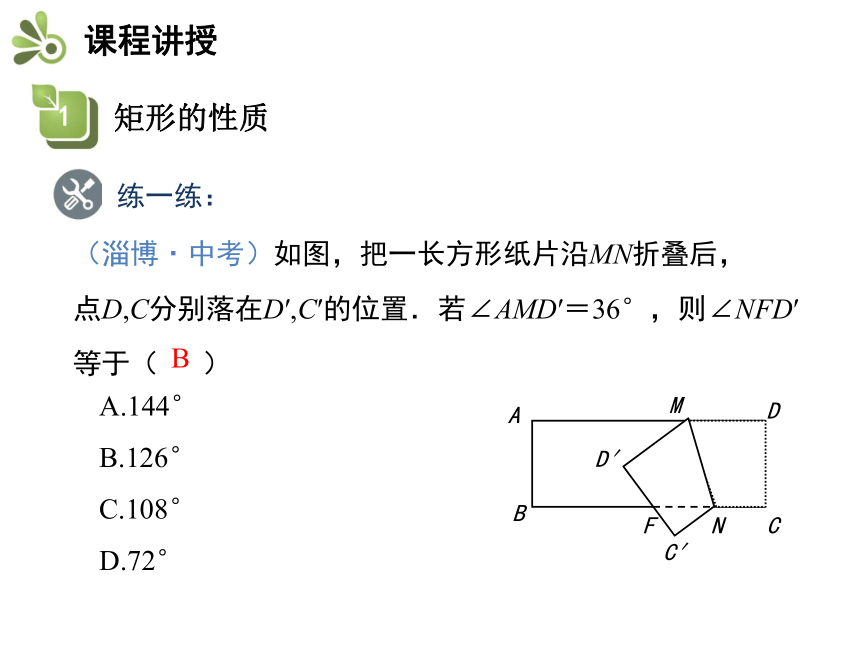
∠A=∠B=∠C=∠D =90°.ABCD练一练:(淄博·中考)如图,把一长方形纸片沿MN折叠后,
点D,C分别落在D′,C′的位置.若∠AMD′=36°,则∠NFD′等于( )A.144° B.126°
C.108° D.72°B 矩形的两条对角线有何关系?证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°.
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB,
∴AC=DB.下面我们对上述猜想进行证明
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与BD相交于点O.求证:AC=DB. 归纳:矩形的对角线相等.
数学表达式:
在矩形ABCD中,
若对角线AC与BD相交于点O,则AC=BD.ABCDO练一练:(中考·怀化)如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6 cm,则AB的长是( )
A.3 cm
B.6 cm
C.10 cm
D.12 cmA证明: 延长BO至D, 使OD=BO,
连接AD,DC. ∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形. ∵∠ABC=90°,∴平行四边形ABCD是矩形,∴AC=BD,D 归纳:直角三角形斜边上的中线等于斜边的一半.练一练:(中考·葫芦岛)如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
A.4
B.8
C.2
D.4D1.矩形具有而平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分A2.( 中考·安顺)如图,在矩形纸片ABCD中,AD=4 cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O. 若AO=5 cm,则AB的长为( )
A.6 cm
B.7 cm
C.8 cm
D.9 cmC3. (中考·鄂尔多斯)如图,P是矩形ABCD的对角线AC
的中点,E是AD的中点.若AB=6,AD=8,则四
边形ABPE的周长为( )
A.14 B.16 C.17 D.18D4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,CE∥DB,交AB的延长线于E.求证:AC=CE.证明:∵四边形ABCD是矩形,∴AC=BD,∴AB∥CD.又∵CE∥DB,∴四边形BECD是平行四边形,∴BD=CE,∴AC=CE.矩形的性质定义:有一个角是直角的平行四边形叫做矩形.具有平行四边形的一切性质四个内角都是直角,
两条对角线相等直角三角形斜边上的中线等于斜边的一半
这节课我们一起来学习一下吧!1.矩形是平行四边形吗?2.平行四边形经过怎样的变化就成为了矩形呢?定义:有一个角是直角的平行四边形叫做矩形.
因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?对于矩形,我们仍然从它的边、角和对角线等方面研究 矩形的四个角有什么特点?ABCD证明:∵四边形ABCD是矩形,
∴∠B=∠D,∠C=∠A, AB∥DC.
∴∠B+∠C=180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B=∠C=∠D=∠A =90°.
下面我们对上述猜想进行证明
如图,四边形ABCD是矩形,∠B=90°.
求证: ∠B=∠C=∠D=∠A=90°.ABCD 归纳:矩形的四个角都是直角.
数学表达式:
在矩形ABCD中,
∠A=∠B=∠C=∠D =90°.ABCD练一练:(淄博·中考)如图,把一长方形纸片沿MN折叠后,
点D,C分别落在D′,C′的位置.若∠AMD′=36°,则∠NFD′等于( )A.144° B.126°
C.108° D.72°B 矩形的两条对角线有何关系?证明:∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°.
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB,
∴AC=DB.下面我们对上述猜想进行证明
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与BD相交于点O.求证:AC=DB. 归纳:矩形的对角线相等.
数学表达式:
在矩形ABCD中,
若对角线AC与BD相交于点O,则AC=BD.ABCDO练一练:(中考·怀化)如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AC=6 cm,则AB的长是( )
A.3 cm
B.6 cm
C.10 cm
D.12 cmA证明: 延长BO至D, 使OD=BO,
连接AD,DC. ∵AO=OC, BO=OD,
∴四边形ABCD是平行四边形. ∵∠ABC=90°,∴平行四边形ABCD是矩形,∴AC=BD,D 归纳:直角三角形斜边上的中线等于斜边的一半.练一练:(中考·葫芦岛)如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
A.4
B.8
C.2
D.4D1.矩形具有而平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分A2.( 中考·安顺)如图,在矩形纸片ABCD中,AD=4 cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O. 若AO=5 cm,则AB的长为( )
A.6 cm
B.7 cm
C.8 cm
D.9 cmC3. (中考·鄂尔多斯)如图,P是矩形ABCD的对角线AC
的中点,E是AD的中点.若AB=6,AD=8,则四
边形ABPE的周长为( )
A.14 B.16 C.17 D.18D4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,CE∥DB,交AB的延长线于E.求证:AC=CE.证明:∵四边形ABCD是矩形,∴AC=BD,∴AB∥CD.又∵CE∥DB,∴四边形BECD是平行四边形,∴BD=CE,∴AC=CE.矩形的性质定义:有一个角是直角的平行四边形叫做矩形.具有平行四边形的一切性质四个内角都是直角,
两条对角线相等直角三角形斜边上的中线等于斜边的一半
