人教版八年级数学下册教学课件:18.2.2 第1课时 菱形的性质(24张)
文档属性
| 名称 | 人教版八年级数学下册教学课件:18.2.2 第1课时 菱形的性质(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 00:00:00 | ||
图片预览




文档简介
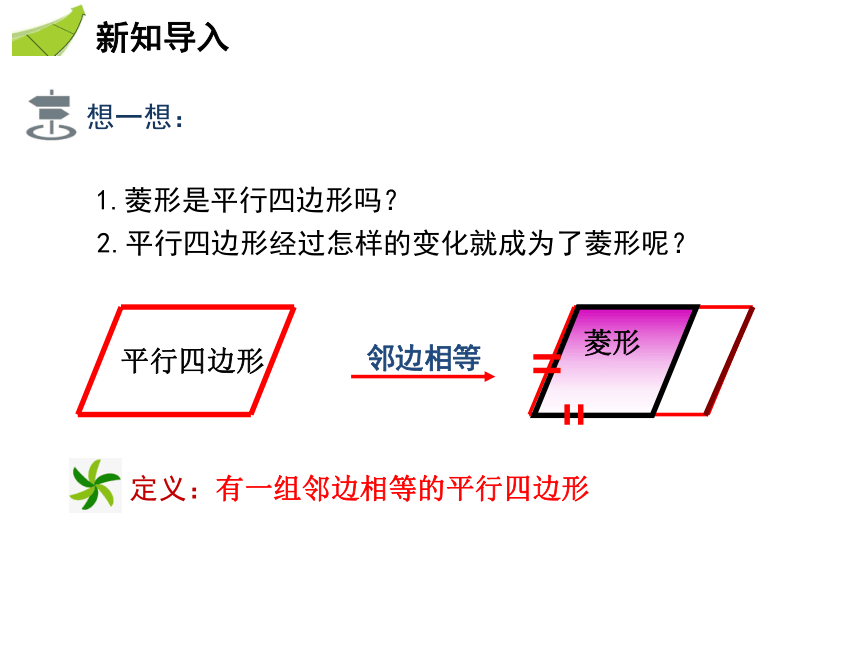
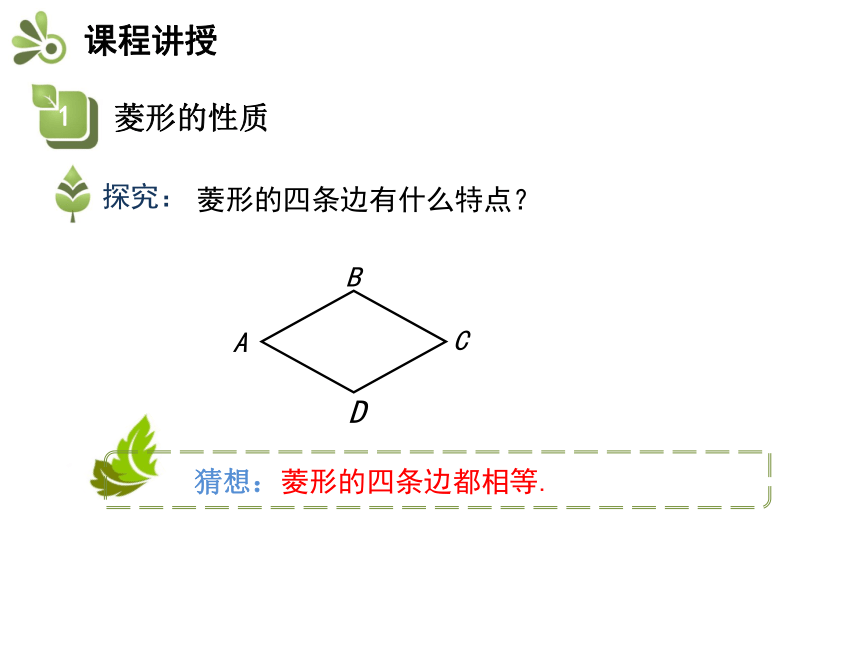
课件24张PPT。知识要点1.菱形的性质2.菱形的面积菱形也是常见的图形,门窗的窗格、美丽的中国结、伸缩的衣帽架等都有菱形的形象,你还能举出一些例子吗?1.菱形是平行四边形吗?2.平行四边形经过怎样的变化就成为了菱形呢?定义:有一组邻边相等的平行四边形 平行四边形 菱形因为菱形是平行四边形,所以它具有平行四边形的所有性质,由于它的一组邻边相等,它是否具有一般平行四边形不具有的一些特殊性质呢?对于菱形,我们仍然从它的边、角和对角线等方面研究 菱形的四条边有什么特点?下面我们对上述猜想进行证明
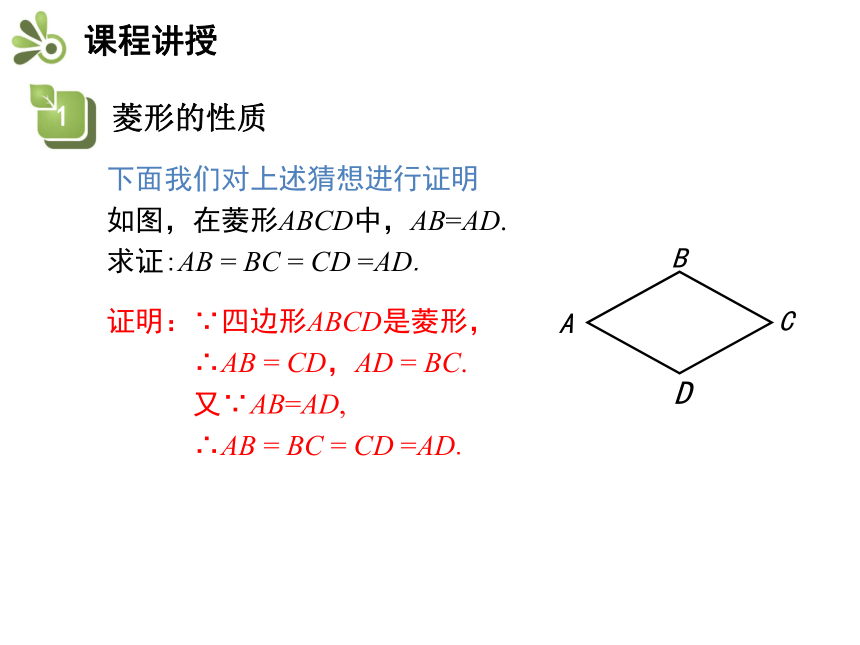
如图,在菱形ABCD中,AB=AD.
求证:AB = BC = CD =AD.
证明:∵四边形ABCD是菱形,
∴AB = CD,AD = BC.
又∵AB=AD,
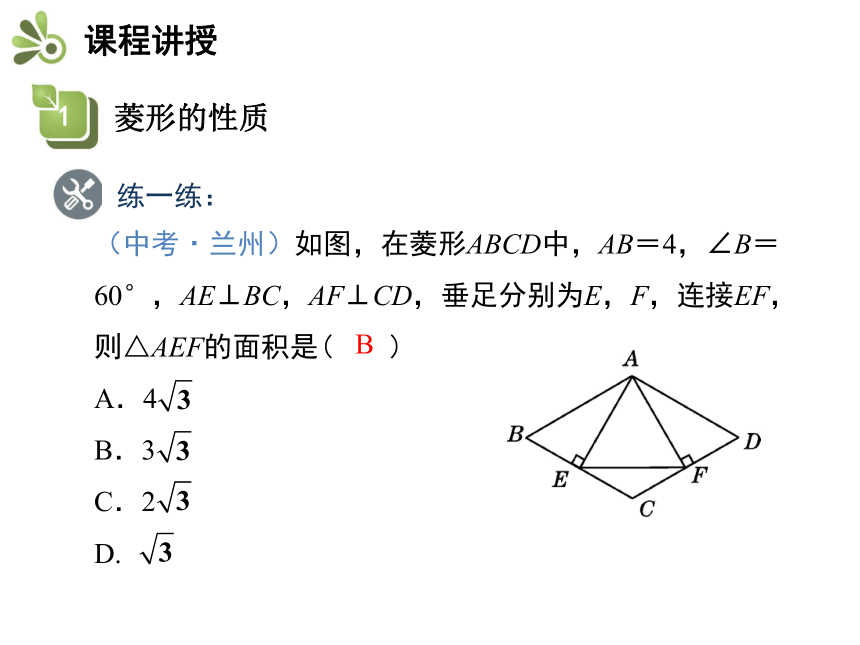
∴AB = BC = CD =AD.AB = BC = CD =AD.练一练:(中考·兰州)如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4
B.3
C.2
D.B 菱形的两条对角线有何关系?下面我们对上述猜想进行证明
如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证 :AC⊥BD, ∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD. (2)∵AB = AD,∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD (菱形的对角线互相平分).
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
练一练:如图,在菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于( )
A.3.5
B.4
C.7
D.14A由菱形两条对角线的长,你能求出它的面积吗?例:如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
解:∵花坛ABCD是菱形,两条小路的长 归纳:菱形的面积计算有如下方法:(1)一边长与两对边的距离(即菱形的高)的积;(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);(3)两条对角线长度乘积的一半.练一练:如图,菱形ABCD的周长是120cm,对角线AC的长度为36cm.求:
(1)另一条对角线的长度;
(2)这个菱形的面积.
练一练:解:(1)∵四边形ABCD是菱形且周长为120cm,∴AB=30cm,AO= AC=18cm,
在RT△ABO中,BO= =24cm,
故BD=2BO=48cm.
(2)这个菱形的面积= AC×BD=864cm2.1.菱形具有而平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等C2.(中考·怀化)如图,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周长为( )
A.20
B.18
C.16
D.15C3.(中考·珠海)如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离是_____cm. 44.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.解:(1)∵四边形ABCD是菱形,∴AC⊥BD.
在RT△OCD中,由勾股定理得OC=4cm .
(2)∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形.
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形.
∵OB=OD=3cm,
∴S矩形OBEC=OB·OC=4×3=12(cm2).菱形的性质定义:有一组邻边相等的平行四边形具有平行四边形的一切性质四条边相等;
对角线互相垂直,并且每一条对角线平分一组对角. 菱形的面积面积=底×高=两条对角线乘积的一半
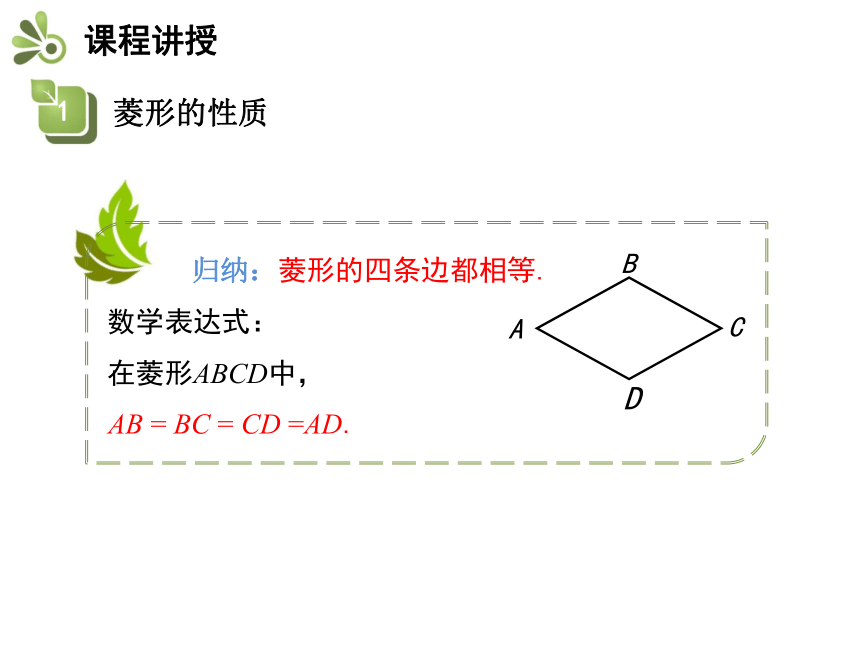
如图,在菱形ABCD中,AB=AD.
求证:AB = BC = CD =AD.
证明:∵四边形ABCD是菱形,
∴AB = CD,AD = BC.
又∵AB=AD,
∴AB = BC = CD =AD.AB = BC = CD =AD.练一练:(中考·兰州)如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4
B.3
C.2
D.B 菱形的两条对角线有何关系?下面我们对上述猜想进行证明
如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证 :AC⊥BD, ∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD. (2)∵AB = AD,∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD (菱形的对角线互相平分).
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.
练一练:如图,在菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于( )
A.3.5
B.4
C.7
D.14A由菱形两条对角线的长,你能求出它的面积吗?例:如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
解:∵花坛ABCD是菱形,两条小路的长 归纳:菱形的面积计算有如下方法:(1)一边长与两对边的距离(即菱形的高)的积;(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);(3)两条对角线长度乘积的一半.练一练:如图,菱形ABCD的周长是120cm,对角线AC的长度为36cm.求:
(1)另一条对角线的长度;
(2)这个菱形的面积.
练一练:解:(1)∵四边形ABCD是菱形且周长为120cm,∴AB=30cm,AO= AC=18cm,
在RT△ABO中,BO= =24cm,
故BD=2BO=48cm.
(2)这个菱形的面积= AC×BD=864cm2.1.菱形具有而平行四边形不具有的性质是( )
A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等C2.(中考·怀化)如图,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周长为( )
A.20
B.18
C.16
D.15C3.(中考·珠海)如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离是_____cm. 44.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.解:(1)∵四边形ABCD是菱形,∴AC⊥BD.
在RT△OCD中,由勾股定理得OC=4cm .
(2)∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形.
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形.
∵OB=OD=3cm,
∴S矩形OBEC=OB·OC=4×3=12(cm2).菱形的性质定义:有一组邻边相等的平行四边形具有平行四边形的一切性质四条边相等;
对角线互相垂直,并且每一条对角线平分一组对角. 菱形的面积面积=底×高=两条对角线乘积的一半
