人教版八年级数学下册教学课件:18.1.2 第1课时 平行四边形的判定1(19张)
文档属性
| 名称 | 人教版八年级数学下册教学课件:18.1.2 第1课时 平行四边形的判定1(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 10:42:12 | ||
图片预览





文档简介
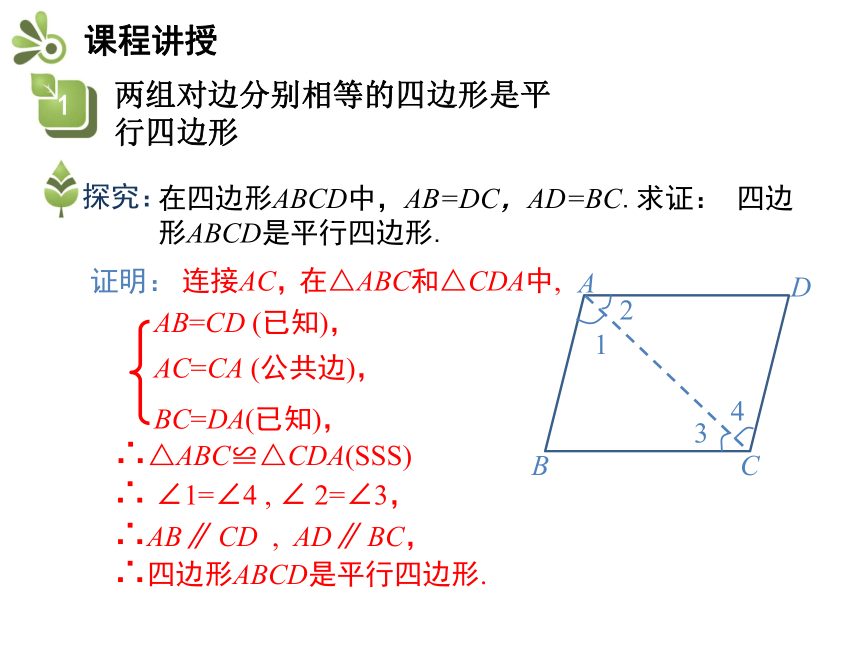
课件19张PPT。知识要点1.两组对边分别相等的四边形是平行 四边形2.两组对角分别相等的四边形是平行四边形3.对角线互相平分的四边形是平行四边形问题2 平行四边形的性质有哪些?问题1 平行四边形的定义是什么?两组对边分别平行的四边形叫平行四边形.平行四边形的对边相等.平行四边形的对角相等.平行四边形的对角线互相平分.在四边形ABCD中,AB=DC,AD=BC.求证: 四边形ABCD是平行四边形.连接AC,在△ABC和△CDA中,AB=CD (已知),BC=DA(已知),AC=CA (公共边),∴△ABC≌△CDA(SSS)∴ ∠1=∠4 , ∠ 2=∠3,∴AB∥ CD , AD∥ BC,∴四边形ABCD是平行四边形.证明:1423ABCD 归纳:方法一:两组对边分别平行的四边形是平
行四边形;(定义法)
数学表达式:如图,∵AB∥CD,
AD∥BC,∴四边形ABCD是平行四边形.
方法二:两组对边分别相等的四边形是平行四边形;
数学表达式:如图,∵AB=CD,AD=BC,∴四边
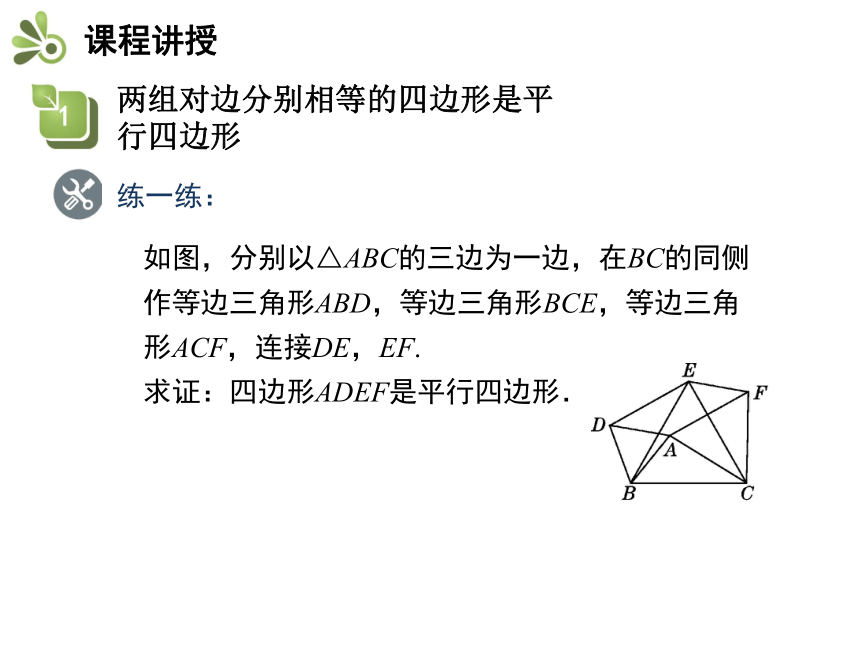
形ABCD是平行四边形.练一练: 如图,分别以△ABC的三边为一边,在BC的同侧
作等边三角形ABD,等边三角形BCE,等边三角
形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.练一练:∵△ABD,△BCE,△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,
∴DE=AC.又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.证明:在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.证明:ABCD又∵∠A=∠C,∠B=∠D,∵∠A+∠C+∠B+∠D=360°,∴2∠A+2∠B=360°,即∠A+∠B=180°,∴ AD∥BC.∴四边形ABCD是平行四边形.同理得 AB∥ CD, 归纳:两组对角分别相等的四边形是平行四边形
数学表达式:
∵∠B=∠D,∠A=∠C,
∴四边形ABCD是平行四边形.练一练:如图,在?ABCD中,BE平分∠ABC,交AD于
点E,DF平分∠ADC,交BC于点F,那么四边
形BFDE是平行四边形吗?为什么?练一练:四边形BFDE是平行四边形.理由如下:
在?ABCD中,∠ABC=∠ADC,∠A=∠C.
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE=∠CBE= ∠ABC,
∠CDF=∠ADF= ∠ADC,
∴∠CDF=∠ADF=∠ABE=∠CBE.
∵∠DFB=∠C+∠CDF,∠BED=∠ABE+∠A,
∴∠DFB=∠BED,∴四边形BFDE是平行四边形.解:四边形ABCD中,OA=OC,OB=OD.求证:四边形ABCD是平行四边形.证明:ABCDO ∵OA=OC,OD=OB,
∠AOD=∠COB,
∴△ AOD≌△COB,
∴∠OAD=∠OCB.
∴AD//BC.
同理得AB//DC.
∴四边形ABCD是平行四边形. 归纳:对角线互相平分的四边形是平行四边形.
数学表达式:
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
练一练: 如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形. 证明:∵四边形ABCD是平行四边形,∴ AO=CO,BO=DO.∵AE=CF ,∴ AO-AE=CO-CF,即EO=OF.又∵BO=DO,∴四边形BFDE是平行四边形.1. 四边形的四条边长分别是a,b,c,d,其中a,b为
一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形B2. 下列给出的条件中,能判定四边形ABCD是平行
四边形的是( )
A.AB∥CD,AD=BC
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.∠B=∠C,∠A=∠DC3.如图,在四边形ABCD中,(1)如果AB∥CD,AD∥BC,那么四边形ABCD是
___________.
(2)如果∠A:∠B:∠ C:∠D=a:b:a:b(a,b为正
数),那么四边形ABCD是__________ .(3)如果AD=6cm,AB=4cm,那么当BC=_______cm,
CD=_____cm时,四边形ABCD为平行四边形. 平行四边形平行四边形_644.如图,AB,CD相交于点O,AC∥DB,AO=BO,E , F 分别是OC,OD的中点.求证:
(1)△AOC≌△BOD;
(2)四边形AFBE是平行四边形.证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD(AAS);
(2)∵△AOC≌△BOD,
∴CO=DO.
∵E , F分别是OC , OD的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE是平行四边形.平行四边形的判定1定义法:两组对边分别平行的四边形叫平行四边形.两组对边分别相等的四边形是平行四边形.对角线互相平分的四边形是平行四边形.两组对角分别相等的四边形是平行四边形.
行四边形;(定义法)
数学表达式:如图,∵AB∥CD,
AD∥BC,∴四边形ABCD是平行四边形.
方法二:两组对边分别相等的四边形是平行四边形;
数学表达式:如图,∵AB=CD,AD=BC,∴四边
形ABCD是平行四边形.练一练: 如图,分别以△ABC的三边为一边,在BC的同侧
作等边三角形ABD,等边三角形BCE,等边三角
形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.练一练:∵△ABD,△BCE,△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,
∴DE=AC.又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.证明:在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.证明:ABCD又∵∠A=∠C,∠B=∠D,∵∠A+∠C+∠B+∠D=360°,∴2∠A+2∠B=360°,即∠A+∠B=180°,∴ AD∥BC.∴四边形ABCD是平行四边形.同理得 AB∥ CD, 归纳:两组对角分别相等的四边形是平行四边形
数学表达式:
∵∠B=∠D,∠A=∠C,
∴四边形ABCD是平行四边形.练一练:如图,在?ABCD中,BE平分∠ABC,交AD于
点E,DF平分∠ADC,交BC于点F,那么四边
形BFDE是平行四边形吗?为什么?练一练:四边形BFDE是平行四边形.理由如下:
在?ABCD中,∠ABC=∠ADC,∠A=∠C.
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE=∠CBE= ∠ABC,
∠CDF=∠ADF= ∠ADC,
∴∠CDF=∠ADF=∠ABE=∠CBE.
∵∠DFB=∠C+∠CDF,∠BED=∠ABE+∠A,
∴∠DFB=∠BED,∴四边形BFDE是平行四边形.解:四边形ABCD中,OA=OC,OB=OD.求证:四边形ABCD是平行四边形.证明:ABCDO ∵OA=OC,OD=OB,
∠AOD=∠COB,
∴△ AOD≌△COB,
∴∠OAD=∠OCB.
∴AD//BC.
同理得AB//DC.
∴四边形ABCD是平行四边形. 归纳:对角线互相平分的四边形是平行四边形.
数学表达式:
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
练一练: 如图, □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形. 证明:∵四边形ABCD是平行四边形,∴ AO=CO,BO=DO.∵AE=CF ,∴ AO-AE=CO-CF,即EO=OF.又∵BO=DO,∴四边形BFDE是平行四边形.1. 四边形的四条边长分别是a,b,c,d,其中a,b为
一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形B2. 下列给出的条件中,能判定四边形ABCD是平行
四边形的是( )
A.AB∥CD,AD=BC
B.AB=AD,CB=CD
C.AB=CD,AD=BC
D.∠B=∠C,∠A=∠DC3.如图,在四边形ABCD中,(1)如果AB∥CD,AD∥BC,那么四边形ABCD是
___________.
(2)如果∠A:∠B:∠ C:∠D=a:b:a:b(a,b为正
数),那么四边形ABCD是__________ .(3)如果AD=6cm,AB=4cm,那么当BC=_______cm,
CD=_____cm时,四边形ABCD为平行四边形. 平行四边形平行四边形_644.如图,AB,CD相交于点O,AC∥DB,AO=BO,E , F 分别是OC,OD的中点.求证:
(1)△AOC≌△BOD;
(2)四边形AFBE是平行四边形.证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD(AAS);
(2)∵△AOC≌△BOD,
∴CO=DO.
∵E , F分别是OC , OD的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE是平行四边形.平行四边形的判定1定义法:两组对边分别平行的四边形叫平行四边形.两组对边分别相等的四边形是平行四边形.对角线互相平分的四边形是平行四边形.两组对角分别相等的四边形是平行四边形.
