人教版八年级数学下册教学课件:19.2.1 第2课时 正比例函数的图象和性质(17张)
文档属性
| 名称 | 人教版八年级数学下册教学课件:19.2.1 第2课时 正比例函数的图象和性质(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 00:00:00 | ||
图片预览






文档简介
课件17张PPT。知识要点1.正比例函数的图象2.正比例函数的性质什么是正比例函数
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
描点法画函数图象的步骤是什么?
列表、描点、连线 经过原点与点(1,k) (k是常数,k≠0)的直线是哪
个函数的图象?画正比例函数的图象时,怎样画最
简单?为什么?
归纳: 因为两点确定一条直线,所以可用两点法画正比例函数y=kx(k≠0)的图象.一般地,过原点和点(1,k)(k是常数,k≠0)的直线,即正比例函数y=kx(k≠0)的图象.例 画出下列正比例函数的图象:
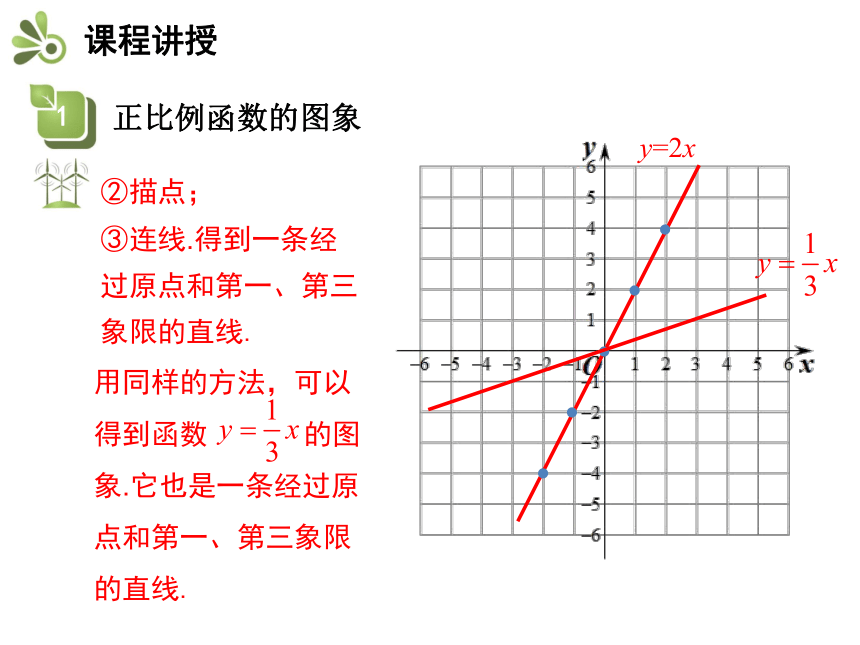
(1)y=2x, ;(2)y =-1.5x,y =-4x.解:(1)函数y=2x中自变量x可为任意实数.
①列表如下:y=2x②描点;③连线.得到一条经
过原点和第一、第三象限的直线.解:(2)函数y =-1.5x中自变量x可为任意实数.
①列表如下:y=-1.5x②描点;③连线.得到一条经
过原点和第二、第四象限的直线.
用同样的方法,可以得到函数 y =-4x 的图象.它也是一条经过原点和第二、第四象限的直线.y=-4x 归纳:
练一练:当x>0时,y与x的函数解析式为y=2x,当x≤0时,y与x的函数解析式为y=-2x,则在同一直角坐标系中的图象大致为( )C 在函数y=2x, ,y =-1.5x,y =-4x中,随着x的增大,y的值分别如何变化?y=2xy=-1.5xy=-4x观察图象可以发现:(1)直线y=2x, 向右逐渐 ,即y的值随x的增大而增大;
(2)直线y=-1.5x,y=-4x向右逐渐 ,即y的值随x的增大而增大而减小. 上升下降练一练:已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )
A.k>5 B.k<5
C.k>-5 D.k<-5D2.对于正比例函数y=-2x,当自变量x的值增加1时,函数y的值增加( )
A. B.-
C.2 D.-21. 正比例函数y=kx(k>0)的图象大致是( )
D D3. 关于函数y=-2x,下列判断正确的是( )
A.图象经过第一、三象限
B.y随x的增大而增大
C.若(x1,y1),(x2,y2)是该函数图象上的两点,
则当x1y2
D.不论x为何值,总有y<0C4. (中考·茂名)如图,三个正比例函数的图象分别对应解析式:①y=ax;②y=bx;③y=cx,将a,b,c从小到大排列并用“<”连接为___________. a<c<b正比例函数的图象和性质正比例函数的图象正比例函数的性质经过原点的直线.
当k>0时,经过第一、三象限;当k<0时,经过第二、四象限.当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
描点法画函数图象的步骤是什么?
列表、描点、连线 经过原点与点(1,k) (k是常数,k≠0)的直线是哪
个函数的图象?画正比例函数的图象时,怎样画最
简单?为什么?
归纳: 因为两点确定一条直线,所以可用两点法画正比例函数y=kx(k≠0)的图象.一般地,过原点和点(1,k)(k是常数,k≠0)的直线,即正比例函数y=kx(k≠0)的图象.例 画出下列正比例函数的图象:
(1)y=2x, ;(2)y =-1.5x,y =-4x.解:(1)函数y=2x中自变量x可为任意实数.
①列表如下:y=2x②描点;③连线.得到一条经
过原点和第一、第三象限的直线.解:(2)函数y =-1.5x中自变量x可为任意实数.
①列表如下:y=-1.5x②描点;③连线.得到一条经
过原点和第二、第四象限的直线.
用同样的方法,可以得到函数 y =-4x 的图象.它也是一条经过原点和第二、第四象限的直线.y=-4x 归纳:
练一练:当x>0时,y与x的函数解析式为y=2x,当x≤0时,y与x的函数解析式为y=-2x,则在同一直角坐标系中的图象大致为( )C 在函数y=2x, ,y =-1.5x,y =-4x中,随着x的增大,y的值分别如何变化?y=2xy=-1.5xy=-4x观察图象可以发现:(1)直线y=2x, 向右逐渐 ,即y的值随x的增大而增大;
(2)直线y=-1.5x,y=-4x向右逐渐 ,即y的值随x的增大而增大而减小. 上升下降练一练:已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )
A.k>5 B.k<5
C.k>-5 D.k<-5D2.对于正比例函数y=-2x,当自变量x的值增加1时,函数y的值增加( )
A. B.-
C.2 D.-21. 正比例函数y=kx(k>0)的图象大致是( )
D D3. 关于函数y=-2x,下列判断正确的是( )
A.图象经过第一、三象限
B.y随x的增大而增大
C.若(x1,y1),(x2,y2)是该函数图象上的两点,
则当x1
D.不论x为何值,总有y<0C4. (中考·茂名)如图,三个正比例函数的图象分别对应解析式:①y=ax;②y=bx;③y=cx,将a,b,c从小到大排列并用“<”连接为___________. a<c<b正比例函数的图象和性质正比例函数的图象正比例函数的性质经过原点的直线.
当k>0时,经过第一、三象限;当k<0时,经过第二、四象限.当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
