人教版数学八年级下册 19.2.2一次函数的图形课件(共15张PPT)
文档属性
| 名称 | 人教版数学八年级下册 19.2.2一次函数的图形课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 773.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 00:26:55 | ||
图片预览



文档简介
(共15张PPT)
玉环市陈屿中学姚正逵
复习回顾
1.一次函数的一般形式
y =kx+b (k,b是常数,k≠0)
正比例函数的一般形式
y=kx (k是常数,k≠0)
二者有什么联系?
正比例函是一次函数b=0时的特殊情况
2.根据函数解析式画图,有哪几步?
列表
描点
连线
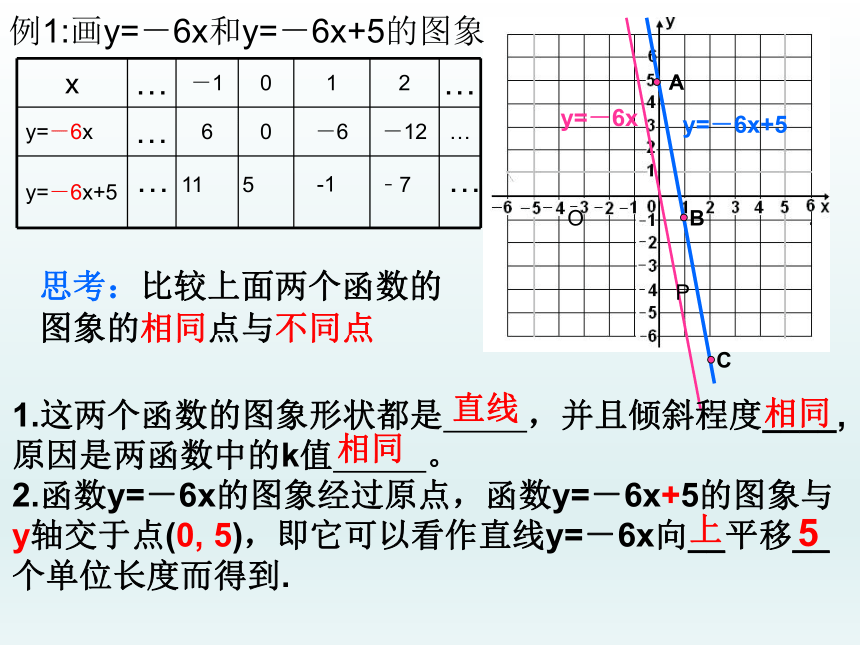
例1:画y=-6x和y=-6x+5的图象
11
5
-1
﹣7
思考:比较上面两个函数的
图象的相同点与不同点
1.这两个函数的图象形状都是 ,并且倾斜程度____,
原因是两函数中的k值 。
2.函数y=-6x的图象经过原点,函数y=-6x+5的图象与
y轴交于点(0, 5),即它可以看作直线y=-6x向__平移__ 个单位长度而得到.
直线
相同
相同
上
5
y=-6x
y=-6x+5
B
C
O
P
A
x … -1 0 1 2 …
y=-6x … 6 0 -6 -12 …
y=-6x+5 … …
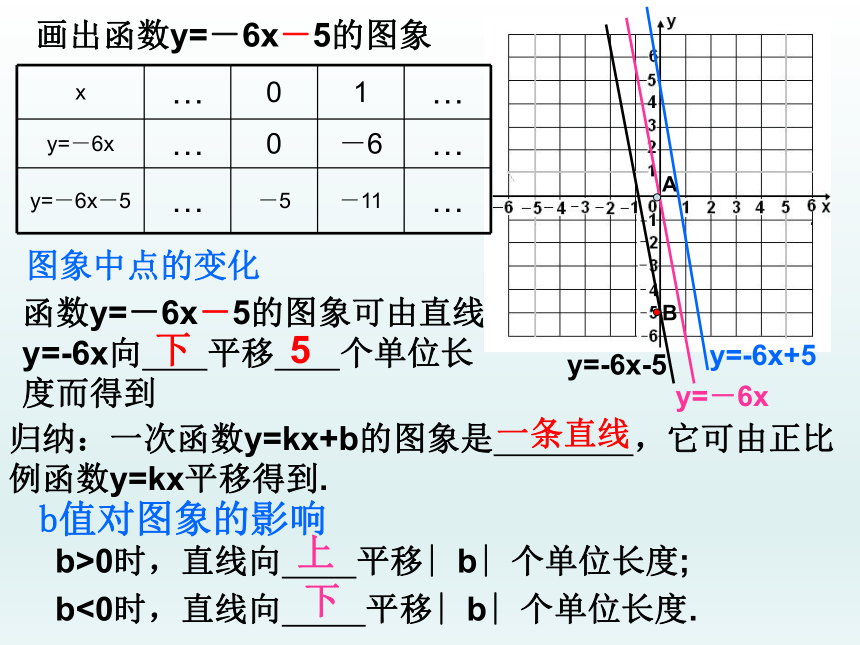
画出函数y=-6x-5的图象
函数y=-6x-5的图象可由直线y=-6x向 平移 个单位长度而得到
y=-6x
y=-6x-5
下
5
图象中点的变化
A
B
归纳:一次函数y=kx+b的图象是 ,它可由正比例函数y=kx平移得到.
b>0时,直线向 平移∣b∣个单位长度;
b<0时,直线向 平移∣b∣个单位长度.
一条直线
上
下
b值对图象的影响
y=-6x+5
x … 0 1 …
y=-6x … 0 -6 …
y=-6x-5 … -5 -11 …
1.将直线y=3x向下平移2个单位得到
直线________。
y=3x-2
2.将直线y=-x-5向上平移5个单位,
得到直线_______。
y=-x
3.函数y=kx-4的图像平行于直线y=-2x,
则其函数的表达式为___________。
y=-2x-4
练习
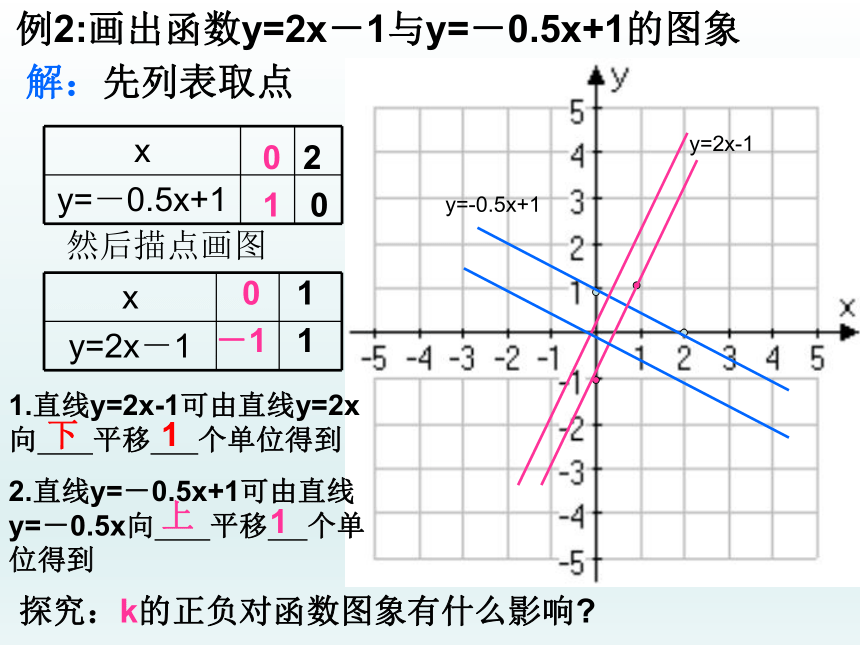
例2:画出函数y=2x-1与y=-0.5x+1的图象
解:先列表取点
然后描点画图
0
-1
1
1
0
1
0
2
y=2x-1
y=-0.5x+1
1.直线y=2x-1可由直线y=2x向 平移 个单位得到
2.直线y=-0.5x+1可由直线y=-0.5x向 平移 个单位得到
下
1
上
1
探究:k的正负对函数图象有什么影响?
x
y=2x-1
x
y=-0.5x+1
在同一平面直角坐标系中画出下列函数的图像
(1)y=-x、y=-x+1与y=-x-2;
(2)y=2x、y=2x+1与y=2x-2.
做一做
思考:画出的图像与上面讨论的结果一样吗?
归纳
这说明了:两条直线是否平行是由解析式中的___决定的,而与y轴的交点位置是由___决定的。
上升,交点在y轴的正半轴.
上升,交点在原点。
上升,交点在y轴的负半轴.
知识归纳
y随x的增大而增大
图象特征 大致图象
k>0 b>0
b=0
b<0
增减性
下降,交点在y轴的正半轴。
下降,交点在原点。
下降,交点在y轴的负半轴。
知识归纳
归纳
K确定直线的
________;
b确定图像与____________________
y轴交点(0,b)的位置.
倾斜方向
y随x的增大而减小
b>0交于正半轴
b<0交于负半轴
图象特征 大致图象
k<0 b>0
b=0
b<0
增减性
⑴.一次函数y=kx+b的图像如图
所示,则k___0,b____0
⑵.函数y=-2x-3的图像通过第
______________象限.
⑶.在函数y=kx+b中,k<0,b>0,
那么这个函数图像不经过第__象限
⑷.已知函数y=kx的图像过(-1,3),
那么k=_____,图像过_______象限
>
<
二、三、四
三
-3
二、四
1、直线y=2x+5与直线y=-3x+5都经过y轴上的
同一点( , )
2、直线y=2x-3,可以由直线y=2x+1向 平移
个单位而得到。直线 y=-3x可以由直线
y=-3x-2 经过向___平移___个单位而得到
3、在一次函数y=(a-3)x-5中,若y随x的增大
而减少,则a的取值范围是 .
4.直线y=kx+b不经过第四象限,则( )
A.k>0,b>0 B.k<0,b>0
C.k>0,b≥0 D.k<0,b≥0
0 5
4
上
a<3
2
下
c
1.直线y= x-3与x轴、y轴的交点分别为A、B,
求该直线与坐标轴围成的三角形面积。
面积专题
令y=0,得x=2,∴A(2,0)
令x=0,得y=-3,∴B(0,-3)
∴OA=2,OB=3
2
-3
2一次函数y=3x+b与两坐标轴围成的三角形面积和为24,求b的值。
面积专题
解:在y=3x+b中,
令x=0,得y=b,∴B(0,b)
∴b2=144,即b=±12
b
y=3x-12
y=3x+12
反思小结:
通过这节课的学习,我们学到了哪些新知识?
1.一次函数的图象是一 条直线.
2.画一次函数图象时,只要取两个点即可,一般取直线与x轴、y轴的交点比较简便.
3.两个一次函数,当k一样,b不一样时,共同之处是直线平行,都是由直线y=kx(k≠0)向上或向下移动得到,不同之处是它们与y轴的交点不同;当b一样,k不一样时,共同之处是它们与y轴交于同一 点(0,b),不同之处是直线不平行
玉环市陈屿中学姚正逵
复习回顾
1.一次函数的一般形式
y =kx+b (k,b是常数,k≠0)
正比例函数的一般形式
y=kx (k是常数,k≠0)
二者有什么联系?
正比例函是一次函数b=0时的特殊情况
2.根据函数解析式画图,有哪几步?
列表
描点
连线
例1:画y=-6x和y=-6x+5的图象
11
5
-1
﹣7
思考:比较上面两个函数的
图象的相同点与不同点
1.这两个函数的图象形状都是 ,并且倾斜程度____,
原因是两函数中的k值 。
2.函数y=-6x的图象经过原点,函数y=-6x+5的图象与
y轴交于点(0, 5),即它可以看作直线y=-6x向__平移__ 个单位长度而得到.
直线
相同
相同
上
5
y=-6x
y=-6x+5
B
C
O
P
A
x … -1 0 1 2 …
y=-6x … 6 0 -6 -12 …
y=-6x+5 … …
画出函数y=-6x-5的图象
函数y=-6x-5的图象可由直线y=-6x向 平移 个单位长度而得到
y=-6x
y=-6x-5
下
5
图象中点的变化
A
B
归纳:一次函数y=kx+b的图象是 ,它可由正比例函数y=kx平移得到.
b>0时,直线向 平移∣b∣个单位长度;
b<0时,直线向 平移∣b∣个单位长度.
一条直线
上
下
b值对图象的影响
y=-6x+5
x … 0 1 …
y=-6x … 0 -6 …
y=-6x-5 … -5 -11 …
1.将直线y=3x向下平移2个单位得到
直线________。
y=3x-2
2.将直线y=-x-5向上平移5个单位,
得到直线_______。
y=-x
3.函数y=kx-4的图像平行于直线y=-2x,
则其函数的表达式为___________。
y=-2x-4
练习
例2:画出函数y=2x-1与y=-0.5x+1的图象
解:先列表取点
然后描点画图
0
-1
1
1
0
1
0
2
y=2x-1
y=-0.5x+1
1.直线y=2x-1可由直线y=2x向 平移 个单位得到
2.直线y=-0.5x+1可由直线y=-0.5x向 平移 个单位得到
下
1
上
1
探究:k的正负对函数图象有什么影响?
x
y=2x-1
x
y=-0.5x+1
在同一平面直角坐标系中画出下列函数的图像
(1)y=-x、y=-x+1与y=-x-2;
(2)y=2x、y=2x+1与y=2x-2.
做一做
思考:画出的图像与上面讨论的结果一样吗?
归纳
这说明了:两条直线是否平行是由解析式中的___决定的,而与y轴的交点位置是由___决定的。
上升,交点在y轴的正半轴.
上升,交点在原点。
上升,交点在y轴的负半轴.
知识归纳
y随x的增大而增大
图象特征 大致图象
k>0 b>0
b=0
b<0
增减性
下降,交点在y轴的正半轴。
下降,交点在原点。
下降,交点在y轴的负半轴。
知识归纳
归纳
K确定直线的
________;
b确定图像与____________________
y轴交点(0,b)的位置.
倾斜方向
y随x的增大而减小
b>0交于正半轴
b<0交于负半轴
图象特征 大致图象
k<0 b>0
b=0
b<0
增减性
⑴.一次函数y=kx+b的图像如图
所示,则k___0,b____0
⑵.函数y=-2x-3的图像通过第
______________象限.
⑶.在函数y=kx+b中,k<0,b>0,
那么这个函数图像不经过第__象限
⑷.已知函数y=kx的图像过(-1,3),
那么k=_____,图像过_______象限
>
<
二、三、四
三
-3
二、四
1、直线y=2x+5与直线y=-3x+5都经过y轴上的
同一点( , )
2、直线y=2x-3,可以由直线y=2x+1向 平移
个单位而得到。直线 y=-3x可以由直线
y=-3x-2 经过向___平移___个单位而得到
3、在一次函数y=(a-3)x-5中,若y随x的增大
而减少,则a的取值范围是 .
4.直线y=kx+b不经过第四象限,则( )
A.k>0,b>0 B.k<0,b>0
C.k>0,b≥0 D.k<0,b≥0
0 5
4
上
a<3
2
下
c
1.直线y= x-3与x轴、y轴的交点分别为A、B,
求该直线与坐标轴围成的三角形面积。
面积专题
令y=0,得x=2,∴A(2,0)
令x=0,得y=-3,∴B(0,-3)
∴OA=2,OB=3
2
-3
2一次函数y=3x+b与两坐标轴围成的三角形面积和为24,求b的值。
面积专题
解:在y=3x+b中,
令x=0,得y=b,∴B(0,b)
∴b2=144,即b=±12
b
y=3x-12
y=3x+12
反思小结:
通过这节课的学习,我们学到了哪些新知识?
1.一次函数的图象是一 条直线.
2.画一次函数图象时,只要取两个点即可,一般取直线与x轴、y轴的交点比较简便.
3.两个一次函数,当k一样,b不一样时,共同之处是直线平行,都是由直线y=kx(k≠0)向上或向下移动得到,不同之处是它们与y轴的交点不同;当b一样,k不一样时,共同之处是它们与y轴交于同一 点(0,b),不同之处是直线不平行
