人教版八年级数学下册教学课件:19.3 课题学习 选择方案(19张)
文档属性
| 名称 | 人教版八年级数学下册教学课件:19.3 课题学习 选择方案(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-30 16:32:45 | ||
图片预览





文档简介
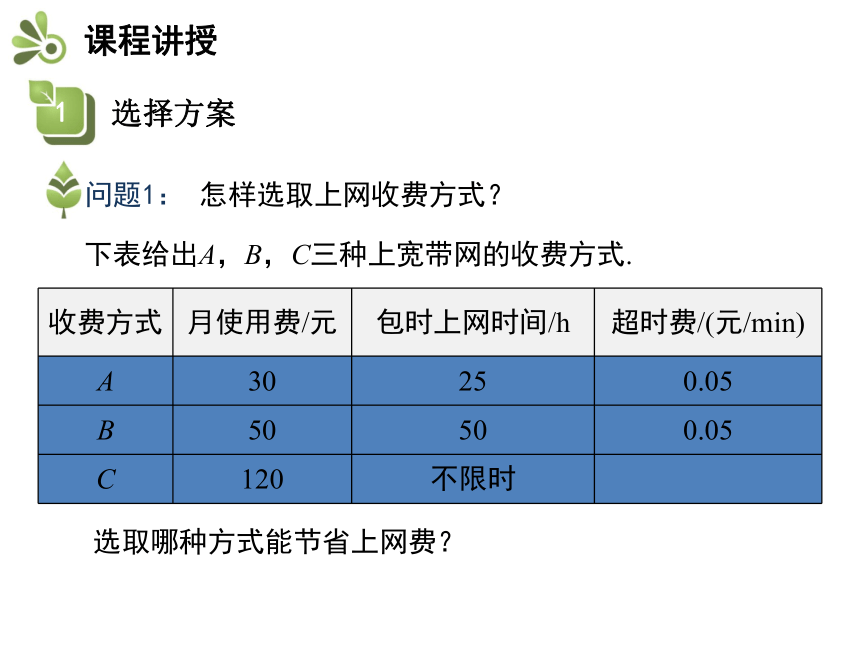
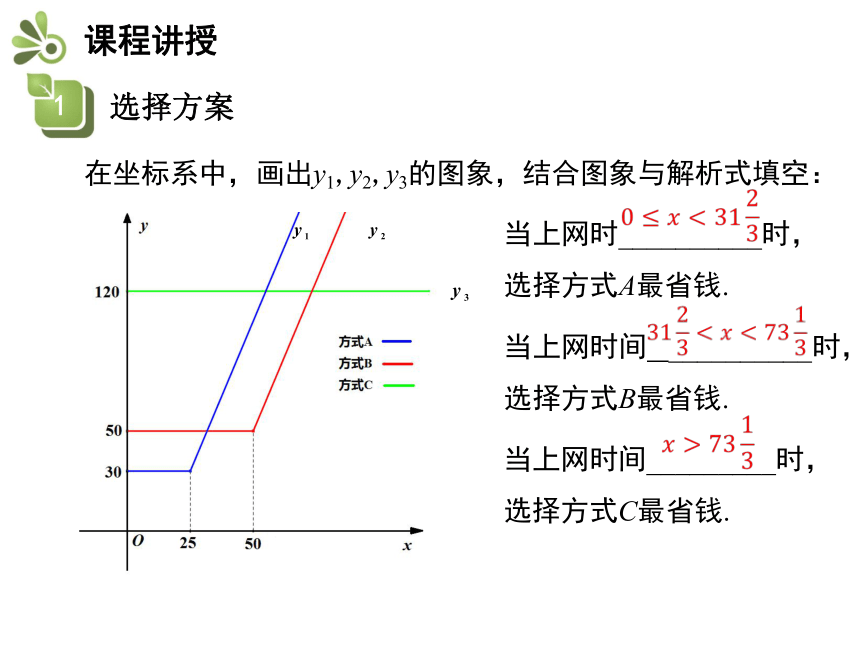
课件19张PPT。知识要点选择方案下表给出A,B,C三种上宽带网的收费方式.选取哪种方式能节省上网费?在方式A中,合起来可写为:当0≤x≤25时,y1=30;当x>25时,y1=30+0.05×60(x-25)=3x-45.当x≥0时,y3=120.在方式B中,在方式C中,在坐标系中,画出y1,y2,y3的图象,结合图象与解析式填空:当上网时__________时,选择方式A最省钱.当上网时间 __________时,选择方式B最省钱.当上网时间_________时,选择方式C最省钱. 练一练: 某单位准备印制一批证书,
现有两个印刷厂可供选择,甲厂费用分
为制版费和印刷费两部分,乙厂直接按
印刷数量收取印刷费.甲、乙两厂的印
刷费用y(元)与证书数量x(个)的函数关系如图所示,下列说法:①甲厂的制版费为1000元;②当印制证书为4000个时,选择乙厂印刷更节省费用;③当印制证书为8000个时,选择乙厂印刷更节省费用.其中正确的有( )
A.0个 B.1个
C.2个 D.3个C某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示:(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.解:(1)240÷45= ,∴最少需要租6辆汽
车.∵每辆汽车上至少有一名教师,∴最多最
多租6辆车,∴共需租6辆汽车.解:设租甲种客车x辆,
①为使240名师生有车坐,②为使租车费用不超过2300元.结合问题的实际意义,共有几种不同的租车方案?为节省费用应选择其中的哪种方案?设租用 x 辆甲种客车,则租车费用y(单位:元)是 x 的函数,即y=400x+280(6-x) =120x+1680.∵x为整数,∴x可取4,5.
由函数可知 y 随 x 增大而增大,所以当 x = 4时 ,y 最小.
ymin=120×4+1680=2160. 练一练:某公司准备与汽车租赁公司签订租车
合同,以每月用车路程x km计算,甲
汽车租赁公司每月收取的租赁费为y1
元,乙汽车租赁公司每月收取的租赁费为y2元.若y1, y2与x之间的函数关系如图所示,其中x = 0对应的函数值为月固定租赁费,则下列说法错误的是_ .(填序号)
练一练:①当月用车路程为2000 km时,两家汽
车租赁公司租赁费用相同;
②当月用车路程为2300 km时,租赁乙
汽车租赁公司的车比较划算;
③除去月固定租赁费,甲租赁公司每公里收取的费用比乙
租赁公司多 ;
④甲租赁公司平均每公里收取的费用比乙租赁公司少.答案:④1.如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法: ①买2件时,甲、乙两家的售价一样;②买1件时,买乙家的划算;③买3件时,买甲家的划算;④买1件时,乙家的产品售价为3元.其中正确的是( )
A.①②
B.①②③
C.②③
D.②③④B2.某书店开展两种方式的租书业务:一种是使用会员 卡,另一种是使用租书卡.使用这两种卡租书,租书 金额y(元)与租书时间x(天)之间的关系如图所示,当租书时间为120天时,使用 卡比较划算.会员3.(2019 ?山西)某游泳馆推出了两种收费方式:
方式一:顾客先购买会员卡,每张会员卡200元,仅限 本人一年内使用,凭卡游泳,每次游泳再付费30 元;
方式二:顾客不购买会员卡,每次游泳付费40 元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).(1)请分别写出y1,y2与x之间的函数解析式;
(2)小亮一年内在此游泳馆游泳的次数x在什么 范围时,选择方式一比方式二省钱?
解:(1)当游泳次数为x时,方式一费用为 y1=30x + 200,方式二的总费用为y2=40x.
(2)由y1 <y2,得 30x + 200<40x,解得 x>20,∴ 当x>20时,选择方式一比方式二省钱.选择方案2. 通过解不等式或画函数图象的方式确定自变量的范围.1. 把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).3. 利用一次函数的增减性知识从而选择出最佳方案.
现有两个印刷厂可供选择,甲厂费用分
为制版费和印刷费两部分,乙厂直接按
印刷数量收取印刷费.甲、乙两厂的印
刷费用y(元)与证书数量x(个)的函数关系如图所示,下列说法:①甲厂的制版费为1000元;②当印制证书为4000个时,选择乙厂印刷更节省费用;③当印制证书为8000个时,选择乙厂印刷更节省费用.其中正确的有( )
A.0个 B.1个
C.2个 D.3个C某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.
现有甲、乙两种大客车,它们的载客量和租金如表所示:(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.解:(1)240÷45= ,∴最少需要租6辆汽
车.∵每辆汽车上至少有一名教师,∴最多最
多租6辆车,∴共需租6辆汽车.解:设租甲种客车x辆,
①为使240名师生有车坐,②为使租车费用不超过2300元.结合问题的实际意义,共有几种不同的租车方案?为节省费用应选择其中的哪种方案?设租用 x 辆甲种客车,则租车费用y(单位:元)是 x 的函数,即y=400x+280(6-x) =120x+1680.∵x为整数,∴x可取4,5.
由函数可知 y 随 x 增大而增大,所以当 x = 4时 ,y 最小.
ymin=120×4+1680=2160. 练一练:某公司准备与汽车租赁公司签订租车
合同,以每月用车路程x km计算,甲
汽车租赁公司每月收取的租赁费为y1
元,乙汽车租赁公司每月收取的租赁费为y2元.若y1, y2与x之间的函数关系如图所示,其中x = 0对应的函数值为月固定租赁费,则下列说法错误的是_ .(填序号)
练一练:①当月用车路程为2000 km时,两家汽
车租赁公司租赁费用相同;
②当月用车路程为2300 km时,租赁乙
汽车租赁公司的车比较划算;
③除去月固定租赁费,甲租赁公司每公里收取的费用比乙
租赁公司多 ;
④甲租赁公司平均每公里收取的费用比乙租赁公司少.答案:④1.如图是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法: ①买2件时,甲、乙两家的售价一样;②买1件时,买乙家的划算;③买3件时,买甲家的划算;④买1件时,乙家的产品售价为3元.其中正确的是( )
A.①②
B.①②③
C.②③
D.②③④B2.某书店开展两种方式的租书业务:一种是使用会员 卡,另一种是使用租书卡.使用这两种卡租书,租书 金额y(元)与租书时间x(天)之间的关系如图所示,当租书时间为120天时,使用 卡比较划算.会员3.(2019 ?山西)某游泳馆推出了两种收费方式:
方式一:顾客先购买会员卡,每张会员卡200元,仅限 本人一年内使用,凭卡游泳,每次游泳再付费30 元;
方式二:顾客不购买会员卡,每次游泳付费40 元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).(1)请分别写出y1,y2与x之间的函数解析式;
(2)小亮一年内在此游泳馆游泳的次数x在什么 范围时,选择方式一比方式二省钱?
解:(1)当游泳次数为x时,方式一费用为 y1=30x + 200,方式二的总费用为y2=40x.
(2)由y1 <y2,得 30x + 200<40x,解得 x>20,∴ 当x>20时,选择方式一比方式二省钱.选择方案2. 通过解不等式或画函数图象的方式确定自变量的范围.1. 把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).3. 利用一次函数的增减性知识从而选择出最佳方案.
