人教版选修4课件 第1章燃烧热 化学反应热的计算(共47张PPT)
文档属性
| 名称 | 人教版选修4课件 第1章燃烧热 化学反应热的计算(共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 化学 | ||
| 更新时间 | 2020-04-30 21:09:13 | ||
图片预览








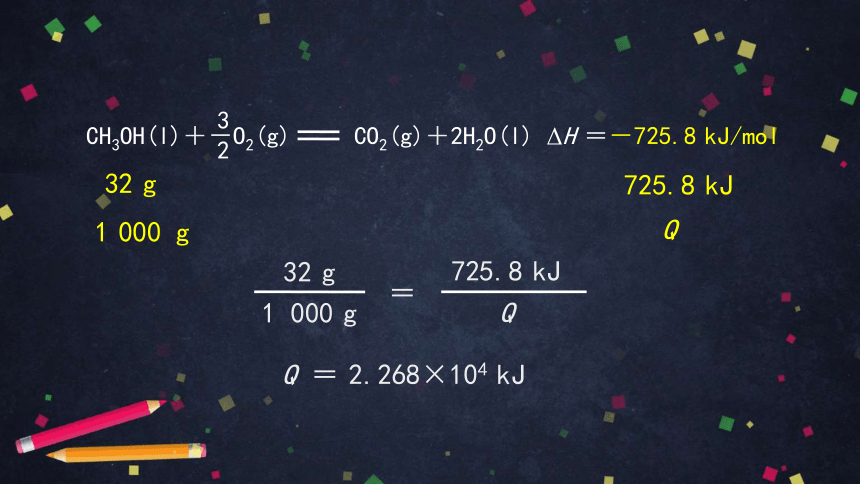
文档简介
(共47张PPT)
第一章 第二节
燃烧热 化学反应热的计算(1)
高二年级 化学
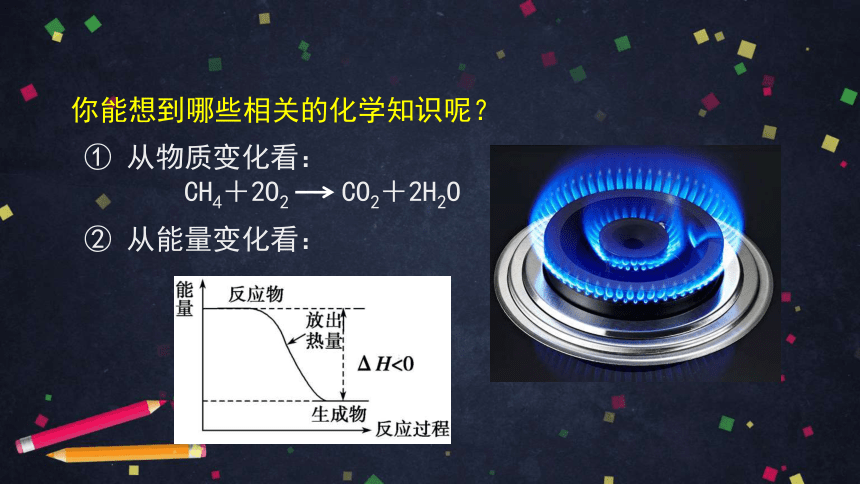
你能想到哪些相关的化学知识呢?
② 从能量变化看:
① 从物质变化看:
CH4+2O2 CO2+2H2O
理论计算:利用键能估算。
量热计
实验测定:
实验测得:在25 ℃、101?kPa时,1?mol?CH4完全燃烧生成液态水和CO2,放出890.3?kJ的热量。
你能写出该反应的热化学方程式吗?
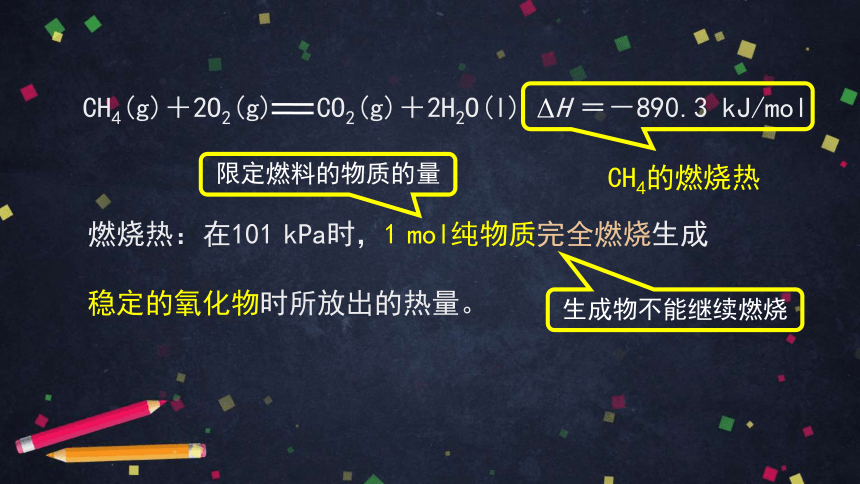
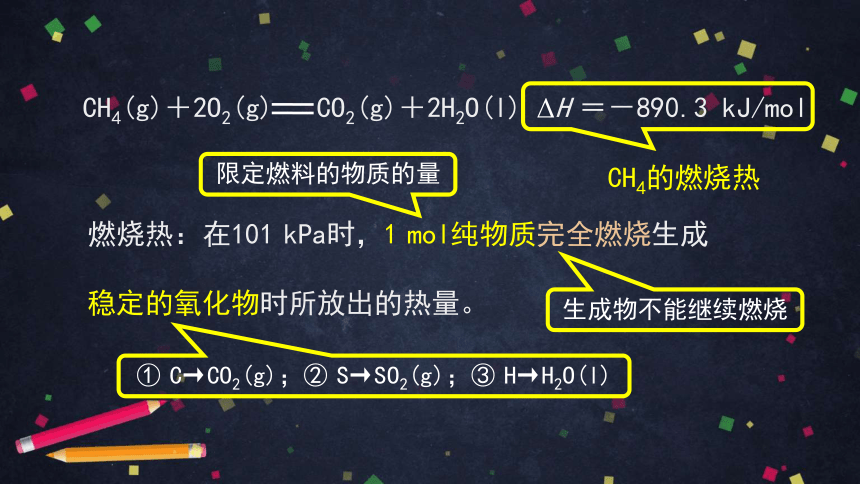
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
CH4的燃烧热
燃烧热:在101 kPa时,1 mol纯物质完全燃烧生成
稳定的氧化物时所放出的热量。
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
CH4的燃烧热
燃烧热:在101 kPa时,1 mol纯物质完全燃烧生成
稳定的氧化物时所放出的热量。
限定燃料的物质的量
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
CH4的燃烧热
燃烧热:在101 kPa时,1 mol纯物质完全燃烧生成
稳定的氧化物时所放出的热量。
限定燃料的物质的量
生成物不能继续燃烧
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
CH4的燃烧热
燃烧热:在101 kPa时,1 mol纯物质完全燃烧生成
稳定的氧化物时所放出的热量。
限定燃料的物质的量
生成物不能继续燃烧
① C→CO2(g);② S→SO2(g);③ H→H2O(l)
1.① 2H2(g)+O2(g) 2H2O(l) ΔH1=-571.6 kJ/mol
② H2(g)+ O2(g) H2O(g) ΔH2=-241.8 kJ/mol
则氢气的燃烧热ΔH = 。
练一练
1
2
-285.8 kJ/mol
名称 化学式 ΔH/(kJ·mol-1) 名称 化学式 ΔH/(kJ·mol-1)
金刚石 C(s) -395.0 石墨 C(s) -393.5
氢气 H2(g) -285.8 乙烷 C2H6(g) -1 559.8
一氧化碳 CO(g) -283.0 乙炔 C2H2(g) -1 299.6
25 ℃、101 kPa,一些物质的燃烧热
2.甲醇是重要的化工原料,又可做为燃料。
已知甲醇的燃烧热ΔH =-725.8 kJ/mol。
根据你对燃烧热的理解,写出甲醇燃烧
的热化学方程式。
并计算25 ℃、101 kPa时,1 kg甲醇完全燃烧放出的热量。
练一练
CH3OH(l)+-O2(g) CO2(g)+2H2O(l) ΔH =-725.8 kJ/mol
3
2
32 g
725.8 kJ
Q
1 000 g
Q = 2.268×104 kJ
CH3OH(l)+-O2(g) CO2(g)+2H2O(l) ΔH =-725.8 kJ/mol
3
2
=
32 g
1 000 g
725.8 kJ
Q
反应热:化学反应中吸收或释放的热量
单位:kJ/mol
中和热:在稀溶液中,酸与碱发生中和反应
生成1 mol H2O(l)时所放出的热量
反应热、燃烧热、中和热的联系与区别
任何反应
中和反应
燃烧热:在101 kPa时,1 mol纯物质完全燃烧
生成稳定的氧化物时所放出的热量
燃烧反应
ΔH = ?
3
2
CH4(g)+-O2(g) CO(g)+2H2O(l)
当家用燃气灶出现黄色火焰时,你有什么好的解决方案?
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
ΔH = ?
3
2
CH4(g)+-O2(g) CO(g)+2H2O(l)
有没有其他方法不需通过实验测定而直接得到?
不管化学反应是一步完成或分几步完成,其反应热是相同的。换句话说,化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关。——盖斯定律
H2SO4 H2SO4·H2O H2SO4·2H2O H2SO4·3H2O
ΔH1
ΔH2
ΔH3
ΔH
盖斯在多次实验中发现,在H2SO4 →H2SO4·3H2O时,无论一步进行还是分步进行,其总的热效应是相同的。
ΔH
为了理解盖斯定律,可以类比登山过程。
登山的高度与上山的途径无关,只与起点和终点的相对高度有关。重力做功也只取决于始终态。
化学反应的反应热也是只与反应的始态和终态有关,而与反应的途径无关。
应用能量守恒论证盖斯定律
盖斯定律是能量守恒定律的必然结果,也是能量守恒定律在化学过程中的应用。
始态S 终态L
ΔH1 < 0
ΔH2 > 0
I Ⅱ
ΔH3
ΔH4
ΔH5
ΔH1+ΔH2 ≡ 0
盖斯定律在科学研究中具有重要意义
(1)有些反应进行得很慢;
(2)有些反应不容易直接发生;
(3)有些反应的产品不纯(有副反应发生)。
这些都给测量反应热造成了困难,利用盖斯定律
可以间接地把它们的反应热计算出来。
盖斯定律的两种具体应用方法
(一)虚拟路径法
ΔH1 =ΔH2+ΔH3
盖斯定律的两种具体应用方法
(一)虚拟路径法
② H2O(l) H2O(g) ΔH2=+44.0 kJ/mol
已知:① H2(g)+-O2(g) H2O(l) ΔH1=-285.8 kJ/mol
1
2
求:③ H2(g)+-O2(g) H2O(g) ΔH3=?
1
2
请同学们利用虚拟路径法计算③的反应热。
盖斯定律的两种具体应用方法
(一)虚拟路径法
H2(g)+-O2(g)
1
2
H2O(g)
ΔH3
盖斯定律的两种具体应用方法
(一)虚拟路径法
ΔH2=+44.0 kJ/mol
H2(g)+-O2(g)
1
2
ΔH1=-285.8 kJ/mol
H2O(g)
H2O(l)
ΔH3
ΔH3=-241.8 kJ/mol
ΔH2=+44.0 kJ/mol
H2(g)+-O2(g)
1
2
盖斯定律的两种具体应用方法
(一)虚拟路径法
H2O(g)
H2O(l)
ΔH3=ΔH1 +ΔH2
ΔH3
ΔH1=-285.8 kJ/mol
ΔH =?
3
2
CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(一)虚拟路径法
CH4(g)+-O2(g)
CO(g)+2H2O(l)
ΔH
(一)虚拟路径法
3
2
CO(g)+2H2O(l)
ΔH
(一)虚拟路径法
CH4(g)+-O2(g)
3
2
ΔH1=-890.3 kJ/mol
CO2(g)+2H2O(l)
CH4(g)+2O2(g)
ΔH1=-890.3 kJ/mol
(一)虚拟路径法
CO2(g)+2H2O(l)
CH4(g)+2O2(g)
ΔH
CO(g)+2H2O(l)+-O2(g)
1
2
ΔH1=-890.3 kJ/mol
(一)虚拟路径法
CO2(g)+2H2O(l)
CH4(g)+2O2(g)
CO(g)+2H2O(l)+-O2(g)
ΔH
1
2
ΔH3=-283.0 kJ/mol
ΔH1=-890.3 kJ/mol
(一)虚拟路径法
CO2(g)+2H2O(l)
CH4(g)+2O2(g)
CO(g)+2H2O(l)+-O2(g)
ΔH
1
2
ΔH3=-283.0 kJ/mol
ΔH =ΔH1- ΔH3=-890.3 kJ/mol-(-283.0 kJ/mol)
=-607.3 kJ/mol
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
① CO(g)+-O2(g) CO2(g) ΔH1=-283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
ΔH3= ?
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
① CO(g)+-O2(g) CO2(g) ΔH1=-283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
ΔH3= ?
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
① CO(g)+-O2(g) CO2(g) ΔH1=-283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
ΔH3= ?
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
④ CO2(g) CO(g)+-O2(g) ΔH4=+283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
④ CO2(g) CO(g)+-O2(g) ΔH4=+283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
+)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
ΔH3=-607.3 kJ/mol
④ CO2(g) CO(g)+-O2(g) ΔH4=+283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
ΔH3=ΔH4+ΔH2
+)
3. 已知金刚石和石墨的燃烧热数据如下,计算石墨转化
为金刚石的反应热。
练一练
名称 化学式 ΔH/(kJ·mol-1) 名称 化学式 ΔH/(kJ·mol-1)
金刚石 C(s) -395.0 石墨 C(s) -393.5
盖斯定律的两种具体应用方法
解法一 虚拟路径法
C(s,石墨)
ΔH
C(s,金刚石)
盖斯定律的两种具体应用方法
解法一 虚拟路径法
C(s,石墨)+O2(g) C(s,金刚石)+O2(g)
CO2(g)
ΔH2=-395.0 kJ/mol
ΔH1=-393.5 kJ/mol
ΔH
盖斯定律的两种具体应用方法
解法一 虚拟路径法
C(s,石墨)+O2(g) C(s,金刚石)+O2(g)
CO2(g)
ΔH2=-395.0 kJ/mol
ΔH1=-393.5 kJ/mol
ΔH1 =ΔH +ΔH2
ΔH =+1.5 kJ/mol
ΔH
① C(s,石墨)+O2(g) CO2(g) ΔH1=-393.5 kJ/mol
② C(s,金刚石)+O2(g) CO2(g) ΔH2=-395.0 kJ/mol
盖斯定律的两种具体应用方法
解法二 热化学方程式叠加法
名称 化学式 ΔH/(kJ·mol-1) 名称 化学式 ΔH/(kJ·mol-1)
金刚石 C(s) -395.0 石墨 C(s) -393.5
③ C(s,石墨) C(s,金刚石)
ΔH3=?
盖斯定律的两种具体应用方法
解法二 热化学方程式叠加法
① C(s,石墨)+O2(g) CO2(g) ΔH1=-393.5 kJ/mol
② C(s,金刚石)+O2(g) CO2(g) ΔH2=-395.0 kJ/mol
① C(s,石墨)+O2(g) CO2(g) ΔH1=-393.5 kJ/mol
④ CO2(g) C(s,金刚石)+O2(g) ΔH2=+395.0 kJ/mol
③ C(s,石墨) C(s,金刚石)
ΔH3=?
盖斯定律的两种具体应用方法
解法二 热化学方程式叠加法
① C(s,石墨)+O2(g) CO2(g) ΔH1=-393.5 kJ/mol
④ CO2(g) C(s,金刚石)+O2(g) ΔH2=+395.0 kJ/mol
③ C(s,石墨) C(s,金刚石)
盖斯定律的两种具体应用方法
解法二 热化学方程式叠加法
+)
ΔH3=+1.5 kJ/mol
“点石成金”,一直是化学家的追求。在20世纪50年代通过高压研究和高压实验技术的发展,这种转化获得了真正的成功。但该转化条件要求极高,产量
很低,金刚石颗粒小,科学家们还在继续研究。
本节课小结
燃烧热:
在101 kPa时,1 mol纯物质完全燃烧生成稳定
的氧化物时所放出的热量。
本节课小结
燃烧热:
盖斯定律:
在101 kPa时,1 mol纯物质完全燃烧生成稳定
的氧化物时所放出的热量。
不管化学反应是一步完成
或分几步完成,其反应热是相同的。
第一章 第二节
燃烧热 化学反应热的计算(1)
高二年级 化学
你能想到哪些相关的化学知识呢?
② 从能量变化看:
① 从物质变化看:
CH4+2O2 CO2+2H2O
理论计算:利用键能估算。
量热计
实验测定:
实验测得:在25 ℃、101?kPa时,1?mol?CH4完全燃烧生成液态水和CO2,放出890.3?kJ的热量。
你能写出该反应的热化学方程式吗?
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
CH4的燃烧热
燃烧热:在101 kPa时,1 mol纯物质完全燃烧生成
稳定的氧化物时所放出的热量。
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
CH4的燃烧热
燃烧热:在101 kPa时,1 mol纯物质完全燃烧生成
稳定的氧化物时所放出的热量。
限定燃料的物质的量
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
CH4的燃烧热
燃烧热:在101 kPa时,1 mol纯物质完全燃烧生成
稳定的氧化物时所放出的热量。
限定燃料的物质的量
生成物不能继续燃烧
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
CH4的燃烧热
燃烧热:在101 kPa时,1 mol纯物质完全燃烧生成
稳定的氧化物时所放出的热量。
限定燃料的物质的量
生成物不能继续燃烧
① C→CO2(g);② S→SO2(g);③ H→H2O(l)
1.① 2H2(g)+O2(g) 2H2O(l) ΔH1=-571.6 kJ/mol
② H2(g)+ O2(g) H2O(g) ΔH2=-241.8 kJ/mol
则氢气的燃烧热ΔH = 。
练一练
1
2
-285.8 kJ/mol
名称 化学式 ΔH/(kJ·mol-1) 名称 化学式 ΔH/(kJ·mol-1)
金刚石 C(s) -395.0 石墨 C(s) -393.5
氢气 H2(g) -285.8 乙烷 C2H6(g) -1 559.8
一氧化碳 CO(g) -283.0 乙炔 C2H2(g) -1 299.6
25 ℃、101 kPa,一些物质的燃烧热
2.甲醇是重要的化工原料,又可做为燃料。
已知甲醇的燃烧热ΔH =-725.8 kJ/mol。
根据你对燃烧热的理解,写出甲醇燃烧
的热化学方程式。
并计算25 ℃、101 kPa时,1 kg甲醇完全燃烧放出的热量。
练一练
CH3OH(l)+-O2(g) CO2(g)+2H2O(l) ΔH =-725.8 kJ/mol
3
2
32 g
725.8 kJ
Q
1 000 g
Q = 2.268×104 kJ
CH3OH(l)+-O2(g) CO2(g)+2H2O(l) ΔH =-725.8 kJ/mol
3
2
=
32 g
1 000 g
725.8 kJ
Q
反应热:化学反应中吸收或释放的热量
单位:kJ/mol
中和热:在稀溶液中,酸与碱发生中和反应
生成1 mol H2O(l)时所放出的热量
反应热、燃烧热、中和热的联系与区别
任何反应
中和反应
燃烧热:在101 kPa时,1 mol纯物质完全燃烧
生成稳定的氧化物时所放出的热量
燃烧反应
ΔH = ?
3
2
CH4(g)+-O2(g) CO(g)+2H2O(l)
当家用燃气灶出现黄色火焰时,你有什么好的解决方案?
CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH =-890.3 kJ/mol
ΔH = ?
3
2
CH4(g)+-O2(g) CO(g)+2H2O(l)
有没有其他方法不需通过实验测定而直接得到?
不管化学反应是一步完成或分几步完成,其反应热是相同的。换句话说,化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关。——盖斯定律
H2SO4 H2SO4·H2O H2SO4·2H2O H2SO4·3H2O
ΔH1
ΔH2
ΔH3
ΔH
盖斯在多次实验中发现,在H2SO4 →H2SO4·3H2O时,无论一步进行还是分步进行,其总的热效应是相同的。
ΔH
为了理解盖斯定律,可以类比登山过程。
登山的高度与上山的途径无关,只与起点和终点的相对高度有关。重力做功也只取决于始终态。
化学反应的反应热也是只与反应的始态和终态有关,而与反应的途径无关。
应用能量守恒论证盖斯定律
盖斯定律是能量守恒定律的必然结果,也是能量守恒定律在化学过程中的应用。
始态S 终态L
ΔH1 < 0
ΔH2 > 0
I Ⅱ
ΔH3
ΔH4
ΔH5
ΔH1+ΔH2 ≡ 0
盖斯定律在科学研究中具有重要意义
(1)有些反应进行得很慢;
(2)有些反应不容易直接发生;
(3)有些反应的产品不纯(有副反应发生)。
这些都给测量反应热造成了困难,利用盖斯定律
可以间接地把它们的反应热计算出来。
盖斯定律的两种具体应用方法
(一)虚拟路径法
ΔH1 =ΔH2+ΔH3
盖斯定律的两种具体应用方法
(一)虚拟路径法
② H2O(l) H2O(g) ΔH2=+44.0 kJ/mol
已知:① H2(g)+-O2(g) H2O(l) ΔH1=-285.8 kJ/mol
1
2
求:③ H2(g)+-O2(g) H2O(g) ΔH3=?
1
2
请同学们利用虚拟路径法计算③的反应热。
盖斯定律的两种具体应用方法
(一)虚拟路径法
H2(g)+-O2(g)
1
2
H2O(g)
ΔH3
盖斯定律的两种具体应用方法
(一)虚拟路径法
ΔH2=+44.0 kJ/mol
H2(g)+-O2(g)
1
2
ΔH1=-285.8 kJ/mol
H2O(g)
H2O(l)
ΔH3
ΔH3=-241.8 kJ/mol
ΔH2=+44.0 kJ/mol
H2(g)+-O2(g)
1
2
盖斯定律的两种具体应用方法
(一)虚拟路径法
H2O(g)
H2O(l)
ΔH3=ΔH1 +ΔH2
ΔH3
ΔH1=-285.8 kJ/mol
ΔH =?
3
2
CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(一)虚拟路径法
CH4(g)+-O2(g)
CO(g)+2H2O(l)
ΔH
(一)虚拟路径法
3
2
CO(g)+2H2O(l)
ΔH
(一)虚拟路径法
CH4(g)+-O2(g)
3
2
ΔH1=-890.3 kJ/mol
CO2(g)+2H2O(l)
CH4(g)+2O2(g)
ΔH1=-890.3 kJ/mol
(一)虚拟路径法
CO2(g)+2H2O(l)
CH4(g)+2O2(g)
ΔH
CO(g)+2H2O(l)+-O2(g)
1
2
ΔH1=-890.3 kJ/mol
(一)虚拟路径法
CO2(g)+2H2O(l)
CH4(g)+2O2(g)
CO(g)+2H2O(l)+-O2(g)
ΔH
1
2
ΔH3=-283.0 kJ/mol
ΔH1=-890.3 kJ/mol
(一)虚拟路径法
CO2(g)+2H2O(l)
CH4(g)+2O2(g)
CO(g)+2H2O(l)+-O2(g)
ΔH
1
2
ΔH3=-283.0 kJ/mol
ΔH =ΔH1- ΔH3=-890.3 kJ/mol-(-283.0 kJ/mol)
=-607.3 kJ/mol
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
① CO(g)+-O2(g) CO2(g) ΔH1=-283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
ΔH3= ?
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
① CO(g)+-O2(g) CO2(g) ΔH1=-283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
ΔH3= ?
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
① CO(g)+-O2(g) CO2(g) ΔH1=-283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
ΔH3= ?
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
④ CO2(g) CO(g)+-O2(g) ΔH4=+283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
④ CO2(g) CO(g)+-O2(g) ΔH4=+283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
+)
盖斯定律的两种具体应用方法
(二)热化学方程式叠加法
ΔH3=-607.3 kJ/mol
④ CO2(g) CO(g)+-O2(g) ΔH4=+283.0 kJ/mol
② CH4(g)+2O2(g) CO2(g)+2H2O(l) ΔH2=-890.3 kJ/mol
1
2
3
2
③ CH4(g)+-O2(g) CO(g)+2H2O(l)
ΔH3=ΔH4+ΔH2
+)
3. 已知金刚石和石墨的燃烧热数据如下,计算石墨转化
为金刚石的反应热。
练一练
名称 化学式 ΔH/(kJ·mol-1) 名称 化学式 ΔH/(kJ·mol-1)
金刚石 C(s) -395.0 石墨 C(s) -393.5
盖斯定律的两种具体应用方法
解法一 虚拟路径法
C(s,石墨)
ΔH
C(s,金刚石)
盖斯定律的两种具体应用方法
解法一 虚拟路径法
C(s,石墨)+O2(g) C(s,金刚石)+O2(g)
CO2(g)
ΔH2=-395.0 kJ/mol
ΔH1=-393.5 kJ/mol
ΔH
盖斯定律的两种具体应用方法
解法一 虚拟路径法
C(s,石墨)+O2(g) C(s,金刚石)+O2(g)
CO2(g)
ΔH2=-395.0 kJ/mol
ΔH1=-393.5 kJ/mol
ΔH1 =ΔH +ΔH2
ΔH =+1.5 kJ/mol
ΔH
① C(s,石墨)+O2(g) CO2(g) ΔH1=-393.5 kJ/mol
② C(s,金刚石)+O2(g) CO2(g) ΔH2=-395.0 kJ/mol
盖斯定律的两种具体应用方法
解法二 热化学方程式叠加法
名称 化学式 ΔH/(kJ·mol-1) 名称 化学式 ΔH/(kJ·mol-1)
金刚石 C(s) -395.0 石墨 C(s) -393.5
③ C(s,石墨) C(s,金刚石)
ΔH3=?
盖斯定律的两种具体应用方法
解法二 热化学方程式叠加法
① C(s,石墨)+O2(g) CO2(g) ΔH1=-393.5 kJ/mol
② C(s,金刚石)+O2(g) CO2(g) ΔH2=-395.0 kJ/mol
① C(s,石墨)+O2(g) CO2(g) ΔH1=-393.5 kJ/mol
④ CO2(g) C(s,金刚石)+O2(g) ΔH2=+395.0 kJ/mol
③ C(s,石墨) C(s,金刚石)
ΔH3=?
盖斯定律的两种具体应用方法
解法二 热化学方程式叠加法
① C(s,石墨)+O2(g) CO2(g) ΔH1=-393.5 kJ/mol
④ CO2(g) C(s,金刚石)+O2(g) ΔH2=+395.0 kJ/mol
③ C(s,石墨) C(s,金刚石)
盖斯定律的两种具体应用方法
解法二 热化学方程式叠加法
+)
ΔH3=+1.5 kJ/mol
“点石成金”,一直是化学家的追求。在20世纪50年代通过高压研究和高压实验技术的发展,这种转化获得了真正的成功。但该转化条件要求极高,产量
很低,金刚石颗粒小,科学家们还在继续研究。
本节课小结
燃烧热:
在101 kPa时,1 mol纯物质完全燃烧生成稳定
的氧化物时所放出的热量。
本节课小结
燃烧热:
盖斯定律:
在101 kPa时,1 mol纯物质完全燃烧生成稳定
的氧化物时所放出的热量。
不管化学反应是一步完成
或分几步完成,其反应热是相同的。
