鲁教版七年级数学下册第八章 平行线的有关证明综合测评(含答案)
文档属性
| 名称 | 鲁教版七年级数学下册第八章 平行线的有关证明综合测评(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-30 09:28:15 | ||
图片预览

文档简介
PAGE
第八章 平行线的有关证明综合测评
(本试卷满分100分)
一、选择题(每小题3分,共24分)
1. 下列语句:①两点之间,直线最短;②不许大声说话;③连接A,B两点;④花儿在春天开放.
其中不是命题的有( )
A.1个 B.2个 C.3个 D.4个
2. 如图1,点E是四边形ABCD的边BC延长线上的一点,则下列条件中不能判定AD∥BE的是( )
A.∠1=∠2 B.∠3=∠4 C.∠D=∠5 D.∠B+∠BAD=180°
图1 图2
3. 在△ABC中,已知∠A=4∠B=104°,则∠C的度数是( )
A.50° B.45° C.40° D.30°
4. 下列命题中,真命题是( )
A.若a2=b2,则a=b B.平方等于其本身的数有0,±1
C.32xy3是4次单项式 D.相等的角是对顶角
5.如图2,下列结论:①若AB∥CD,则∠3=∠4;②若∠1=∠BEG,则EF∥GH;③若∠FGH+∠3=180°,则EF∥GH;④若AB∥CD,∠4=62°,EG平分∠BEF,则∠1=59°.其中正确的是( )
A.仅①③ B. 仅①③④ C. 仅①④ D. ①②③④
6. 下列各数中,说明命题“任何偶数都是6的倍数”是假命题的反例是( )
A.16 B.12 C.18 D.9
7. 如图3,从①∠1=∠2 ,②∠C=∠D, ③∠A=∠F中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
A.0 B.1
C.2 D.3
图3 图4
8. 如图4,已知点P为△ABC三条内角平分线AD,BE,CF的交点,作DG⊥PC于点G,则∠PDG等于( )
A.∠ABE B.∠DAC C.∠BCF D.∠CPE
二、填空题(每小题4分,共32分)
9. 把命题“同角的余角相等”改写成“如果……那么……”的形式是 .
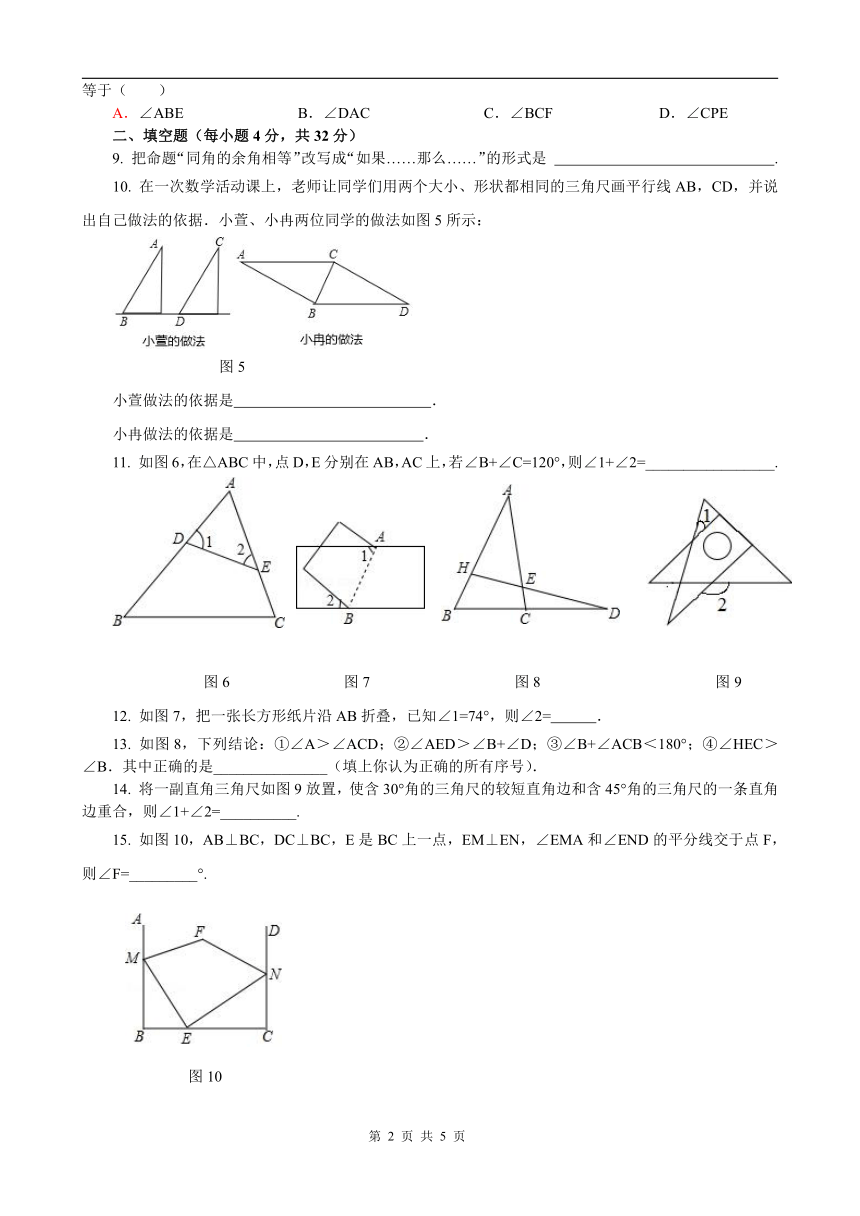
10. 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角尺画平行线AB,CD,并说出自己做法的依据.小萱、小冉两位同学的做法如图5所示:
图5
小萱做法的依据是 .
小冉做法的依据是 .
11. 如图6,在△ABC中,点D,E分别在AB,AC上,若∠B+∠C=120°,则∠1+∠2=_________________.
图6 图7 图8 图9
12. 如图7,把一张长方形纸片沿AB折叠,已知∠1=74°,则∠2= .
13. 如图8,下列结论:①∠A>∠ACD;②∠AED>∠B+∠D;③∠B+∠ACB<180°;④∠HEC>∠B.其中正确的是_______________(填上你认为正确的所有序号).
14. 将一副直角三角尺如图9放置,使含30°角的三角尺的较短直角边和含45°角的三角尺的一条直角边重合,则∠1+∠2=__________.
15. 如图10,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,则∠F=_________°.
图10
16. 甲、乙、丙、丁四个小朋友在院里玩球,忽听“砰”的一声,球击中了李大爷家的窗户.李大爷跑出来查看,发现一块窗户玻璃被打裂了.李大爷问:“是谁闯的祸?”
甲说:“是乙不小心闯的祸.”乙说:“是丙闯的祸.”
丙说:“乙说的不是真话.”丁说:“反正不是我闯的祸.”
如果这四个小朋友中只有一个人说了真话,请你帮李大爷判断一下,闯祸的是__________.
三、解答题(共44分)
17.(8分)如图11,已知CD与BH相交于点G,∠B=∠BGD,∠DGF=∠BFE,求证:∠B=∠EFH.
(请先完成下面的填空,再继续完成此题的证明.)
图11
证明:因为∠B=∠BGD(已知),
所以AB∥CD(_______________________).
18.(10分)如图12,在△ABC中,AD平分∠BAC,DE∥AC,且∠EAD=14°,∠ABC=62°,试判断△BDE的形状,并说明理由.
图12
19.(12分)如图13,△ABC中,AD平分∠BAC,EF交BA延长线于点G,∠3=∠G.
(1)求证:AD∥EG;
(2)设∠B=x,∠G=y,若x-y=30°,∠ADC=110°,求∠B的度数.
图13
20.(14分)如图14-①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图14-②,过点P作直线MN,分别交AB和AC于点M,N,且MN平行于BC,则有∠MPB+∠NPC=90°-∠A.若将直线MN绕点P旋转,
(ⅰ)如图14-③,试探索∠MPB,∠NPC,∠A三者之间的数量关系是否依然成立,并说明理由;
(ⅱ)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图14-④,试问(ⅰ)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明理由.
① ② ③ ④
图14
第八章 平行线的有关证明综合测评
一、1. B 2. A 3. A 4.C 5. B 6.A 7. D 8. A
二、9. 如果两个角是同一个角的余角,那么这两个角相等
10. 同位角相等,两直线平行 内错角相等,两直线平行 11. 120° 12.32° 13. ②③④
14. 165° 15.135 16. 丁
三、17. 解:内错角相等,两直线平行
因为∠DGF=∠BFE,所以CD∥EF.所以AB∥EF.所以∠B=∠EFH.
18. 解:△BDE是直角三角形.
理由:因为AD平分∠BAC,所以∠BAC=2∠EAD=28°.
因为DE∥AC,所以∠BED=∠BAC=28°.
因为∠ABC+∠BED+∠BDE=180°,∠ABC=62°,所以∠BDE=180°-62°-28°=90°.
所以△BDE是直角三角形.
19.(1)证明:因为AD平分∠BAC,所以∠1=∠2.
因为∠3=∠G,∠3=∠4,所以∠4=∠G.
因为∠BAC=∠G+∠4=2∠4,∠BAC=∠1+∠2=2∠2,所以∠2=∠4.
所以∠2=∠4.所以AD∥EG.
(2)解:因为AD∥EG,所以∠1=∠G=y.因为∠ADC=∠B+∠1=110°,所以x+y=110°.
所以,解得.所以∠B=70°.
20. 解:(1)如图①,因为在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=80°,所以∠ABC+∠ACB=100°.
所以∠BPC=180°-(∠PBC+∠PCB)=180°-(∠ABC+∠ACB)=180°-×100°=130°.
(2)(ⅰ)成立.理由:如图③,由(1)知∠BPC=180°-(∠PBC +∠PCB).
因为∠PBC +∠PCB =(180°-∠A)=90°?∠A,所以∠BPC=180°-(90°-∠A)=90°+∠A.
所以∠MPB+∠NPC=180°-∠BPC=180°-(90°+∠A)=90°-∠A.
(ⅱ)不成立,∠MPB-∠NPC=90°-∠A.
理由:由(ⅰ)知∠BPC=90°+∠A.
所以∠MPB-∠NPC=180°-∠BPC=180°-(90°+∠A)=90°-∠A.
提醒语:请同学们继续完成此题的证明.
PAGE
第 2 页 共 5 页
第八章 平行线的有关证明综合测评
(本试卷满分100分)
一、选择题(每小题3分,共24分)
1. 下列语句:①两点之间,直线最短;②不许大声说话;③连接A,B两点;④花儿在春天开放.
其中不是命题的有( )
A.1个 B.2个 C.3个 D.4个
2. 如图1,点E是四边形ABCD的边BC延长线上的一点,则下列条件中不能判定AD∥BE的是( )
A.∠1=∠2 B.∠3=∠4 C.∠D=∠5 D.∠B+∠BAD=180°
图1 图2
3. 在△ABC中,已知∠A=4∠B=104°,则∠C的度数是( )
A.50° B.45° C.40° D.30°
4. 下列命题中,真命题是( )
A.若a2=b2,则a=b B.平方等于其本身的数有0,±1
C.32xy3是4次单项式 D.相等的角是对顶角
5.如图2,下列结论:①若AB∥CD,则∠3=∠4;②若∠1=∠BEG,则EF∥GH;③若∠FGH+∠3=180°,则EF∥GH;④若AB∥CD,∠4=62°,EG平分∠BEF,则∠1=59°.其中正确的是( )
A.仅①③ B. 仅①③④ C. 仅①④ D. ①②③④
6. 下列各数中,说明命题“任何偶数都是6的倍数”是假命题的反例是( )
A.16 B.12 C.18 D.9
7. 如图3,从①∠1=∠2 ,②∠C=∠D, ③∠A=∠F中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )
A.0 B.1
C.2 D.3
图3 图4
8. 如图4,已知点P为△ABC三条内角平分线AD,BE,CF的交点,作DG⊥PC于点G,则∠PDG等于( )
A.∠ABE B.∠DAC C.∠BCF D.∠CPE
二、填空题(每小题4分,共32分)
9. 把命题“同角的余角相等”改写成“如果……那么……”的形式是 .
10. 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角尺画平行线AB,CD,并说出自己做法的依据.小萱、小冉两位同学的做法如图5所示:
图5
小萱做法的依据是 .
小冉做法的依据是 .
11. 如图6,在△ABC中,点D,E分别在AB,AC上,若∠B+∠C=120°,则∠1+∠2=_________________.
图6 图7 图8 图9
12. 如图7,把一张长方形纸片沿AB折叠,已知∠1=74°,则∠2= .
13. 如图8,下列结论:①∠A>∠ACD;②∠AED>∠B+∠D;③∠B+∠ACB<180°;④∠HEC>∠B.其中正确的是_______________(填上你认为正确的所有序号).
14. 将一副直角三角尺如图9放置,使含30°角的三角尺的较短直角边和含45°角的三角尺的一条直角边重合,则∠1+∠2=__________.
15. 如图10,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,则∠F=_________°.
图10
16. 甲、乙、丙、丁四个小朋友在院里玩球,忽听“砰”的一声,球击中了李大爷家的窗户.李大爷跑出来查看,发现一块窗户玻璃被打裂了.李大爷问:“是谁闯的祸?”
甲说:“是乙不小心闯的祸.”乙说:“是丙闯的祸.”
丙说:“乙说的不是真话.”丁说:“反正不是我闯的祸.”
如果这四个小朋友中只有一个人说了真话,请你帮李大爷判断一下,闯祸的是__________.
三、解答题(共44分)
17.(8分)如图11,已知CD与BH相交于点G,∠B=∠BGD,∠DGF=∠BFE,求证:∠B=∠EFH.
(请先完成下面的填空,再继续完成此题的证明.)
图11
证明:因为∠B=∠BGD(已知),
所以AB∥CD(_______________________).
18.(10分)如图12,在△ABC中,AD平分∠BAC,DE∥AC,且∠EAD=14°,∠ABC=62°,试判断△BDE的形状,并说明理由.
图12
19.(12分)如图13,△ABC中,AD平分∠BAC,EF交BA延长线于点G,∠3=∠G.
(1)求证:AD∥EG;
(2)设∠B=x,∠G=y,若x-y=30°,∠ADC=110°,求∠B的度数.
图13
20.(14分)如图14-①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图14-②,过点P作直线MN,分别交AB和AC于点M,N,且MN平行于BC,则有∠MPB+∠NPC=90°-∠A.若将直线MN绕点P旋转,
(ⅰ)如图14-③,试探索∠MPB,∠NPC,∠A三者之间的数量关系是否依然成立,并说明理由;
(ⅱ)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图14-④,试问(ⅰ)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明理由.
① ② ③ ④
图14
第八章 平行线的有关证明综合测评
一、1. B 2. A 3. A 4.C 5. B 6.A 7. D 8. A
二、9. 如果两个角是同一个角的余角,那么这两个角相等
10. 同位角相等,两直线平行 内错角相等,两直线平行 11. 120° 12.32° 13. ②③④
14. 165° 15.135 16. 丁
三、17. 解:内错角相等,两直线平行
因为∠DGF=∠BFE,所以CD∥EF.所以AB∥EF.所以∠B=∠EFH.
18. 解:△BDE是直角三角形.
理由:因为AD平分∠BAC,所以∠BAC=2∠EAD=28°.
因为DE∥AC,所以∠BED=∠BAC=28°.
因为∠ABC+∠BED+∠BDE=180°,∠ABC=62°,所以∠BDE=180°-62°-28°=90°.
所以△BDE是直角三角形.
19.(1)证明:因为AD平分∠BAC,所以∠1=∠2.
因为∠3=∠G,∠3=∠4,所以∠4=∠G.
因为∠BAC=∠G+∠4=2∠4,∠BAC=∠1+∠2=2∠2,所以∠2=∠4.
所以∠2=∠4.所以AD∥EG.
(2)解:因为AD∥EG,所以∠1=∠G=y.因为∠ADC=∠B+∠1=110°,所以x+y=110°.
所以,解得.所以∠B=70°.
20. 解:(1)如图①,因为在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=80°,所以∠ABC+∠ACB=100°.
所以∠BPC=180°-(∠PBC+∠PCB)=180°-(∠ABC+∠ACB)=180°-×100°=130°.
(2)(ⅰ)成立.理由:如图③,由(1)知∠BPC=180°-(∠PBC +∠PCB).
因为∠PBC +∠PCB =(180°-∠A)=90°?∠A,所以∠BPC=180°-(90°-∠A)=90°+∠A.
所以∠MPB+∠NPC=180°-∠BPC=180°-(90°+∠A)=90°-∠A.
(ⅱ)不成立,∠MPB-∠NPC=90°-∠A.
理由:由(ⅰ)知∠BPC=90°+∠A.
所以∠MPB-∠NPC=180°-∠BPC=180°-(90°+∠A)=90°-∠A.
提醒语:请同学们继续完成此题的证明.
PAGE
第 2 页 共 5 页
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
