鲁教版七年级数学下册第八章 平行线的有关证明综合测评(含答案)
文档属性
| 名称 | 鲁教版七年级数学下册第八章 平行线的有关证明综合测评(含答案) | 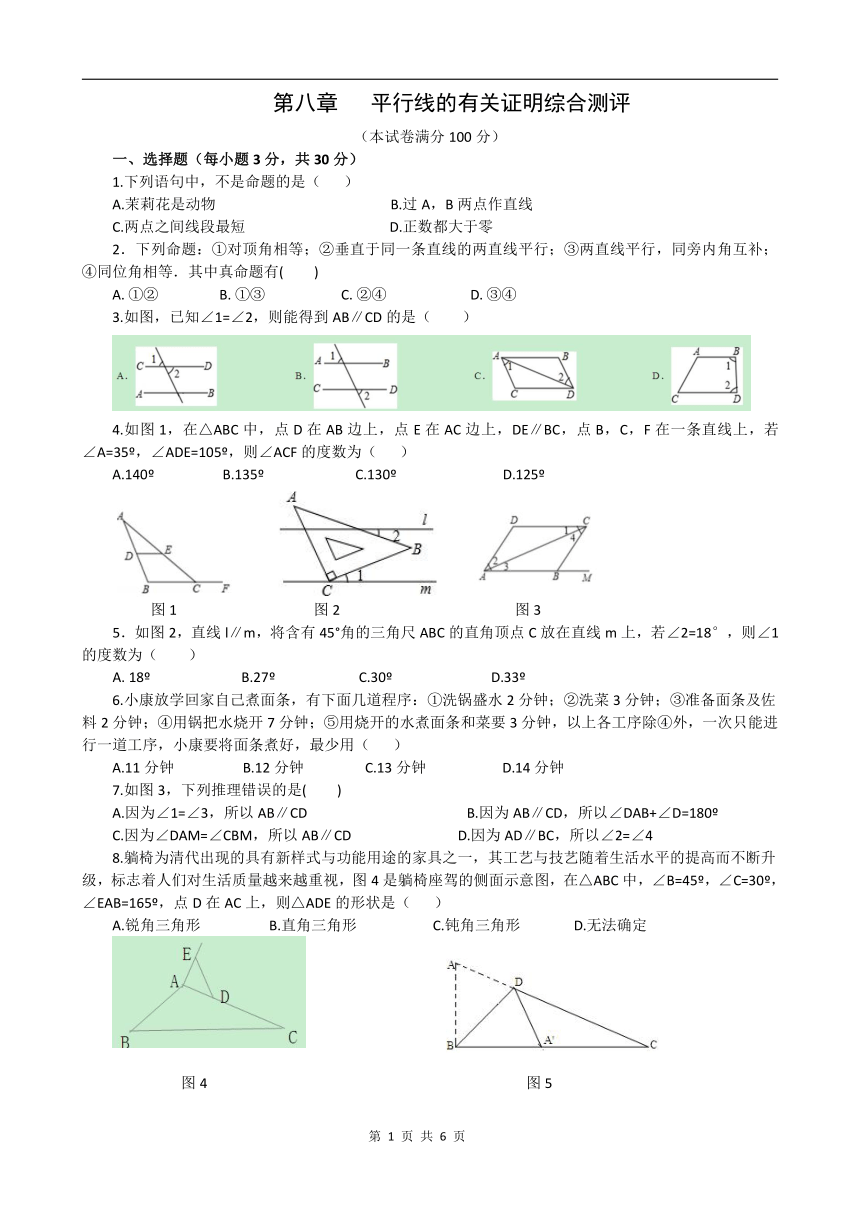 | |
| 格式 | zip | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-30 09:23:42 | ||
图片预览



文档简介
PAGE
第八章 平行线的有关证明综合测评
(本试卷满分100分)
一、选择题(每小题3分,共30分)
1.下列语句中,不是命题的是( )
A.茉莉花是动物 B.过A,B两点作直线
C.两点之间线段最短 D.正数都大于零
2.下列命题:①对顶角相等;②垂直于同一条直线的两直线平行;③两直线平行,同旁内角互补;④同位角相等.其中真命题有( )
A. ①② B. ①③ C. ②④ D. ③④
3.如图,已知∠1=∠2,则能得到AB∥CD的是( )
4.如图1,在△ABC中,点D在AB边上,点E在AC边上,DE∥BC,点B,C,F在一条直线上,若∠A=35?,∠ADE=105?,则∠ACF的度数为( )
A.140? B.135? C.130? D.125?
图1 图2 图3
5.如图2,直线l∥m,将含有45°角的三角尺ABC的直角顶点C放在直线m上,若∠2=18°,则∠1的度数为( )
A. 18? B.27? C.30? D.33?
6.小康放学回家自己煮面条,有下面几道程序:①洗锅盛水2分钟;②洗菜3分钟;③准备面条及佐料2分钟;④用锅把水烧开7分钟;⑤用烧开的水煮面条和菜要3分钟,以上各工序除④外,一次只能进行一道工序,小康要将面条煮好,最少用( )
A.11分钟 B.12分钟 C.13分钟 D.14分钟
7.如图3,下列推理错误的是( )
A.因为∠1=∠3,所以AB∥CD B.因为AB∥CD,所以∠DAB+∠D=180?
C.因为∠DAM=∠CBM,所以AB∥CD D.因为AD∥BC,所以∠2=∠4
8.躺椅为清代出现的具有新样式与功能用途的家具之一,其工艺与技艺随着生活水平的提高而不断升级,标志着人们对生活质量越来越重视,图4是躺椅座驾的侧面示意图,在△ABC中,∠B=45?,∠C=30?,∠EAB=165?,点D在AC上,则△ADE的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
图4 图5
9.如图5,在△ABC中,∠ABC=90°,∠C=24°,D是AC上一点.将△ABC沿BD折叠,使点A落在BC边上的A′处,则∠A′DC的度数为( )
A. 42° B. 40° C. 30° D. 24°
10.如图6,在△ABC中,BD,BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠BGH=∠ABE+∠C.
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
图6
二、填空题(每小题3分,共18分)
11.命题“直角三角形的两锐角互余”的条件是 .
12.如图7,已知AD∥BC,∠1=30?,∠BAC=32?,则∠B=_____.
图7 图8
13.将一条两边互相平行的纸带按图8所示折叠,∠2=36°,则∠1的度数为_______°.
14.如图9-①,“和谐号”高铁列车的小桌板收起来近似看做与地面垂直,展开小桌板使桌面保持水平.图9-②是小桌板展开后的示意图,其中OB表示小桌板桌面的宽度,BC表示小桌板的支架,∠AOB=∠ACB=37?,∠OAC=46?,则∠OBC的度数是______.
1 ②
图9 图10 图11
15.将一副三角尺按图10所示放置,则下列结论:①若∠2=30?,则AC∥DE;②若BC∥AD,则∠2=30?;
③若∠CAD=150?,则∠4=∠C;④∠BAE+∠CAD=180?.其中正确的有_____(填序号).
16. 如图11,在四边形ABCD中,∠A+∠B=200°.作∠ADC,∠BCD的平分线交于点O1,称为第1次操作;作∠O1DC,∠O1CD的平分线交于点O2,称为第2次操作;作∠O2DC,∠O2CD的平分线交于点O3,称为第3次操作;……则第6次操作后∠CO6D的度数是____________.
三、解答题(共52分)
17. (6分)如图12,在△ABC 中,∠B=45°,∠C=38°,E是BC边上一点,ED交CA的延长线于点D,交AB于点F,∠D=32°.求∠AFE的大小.
18.(8分)如图13,已知∠1=∠C,∠3=∠4,求证:∠2=∠5.
图13
19.(8分)下列命题是真命题,还是假命题?如果是假命题,请举出反例.
(1)带根号的数都是无理数;
(2)三条线段a,b,c,若a+b>c,那么这三条线段一定能组成三角形;
(3)同一个平面内,不相交的两条直线一定平行.
(4)若两个数的绝对值相等,那么这两个数一定相等.
20.(9分)如图14,在△ABC中,D是BC边上的点,∠1=∠2,∠3=∠4,∠BAC=63?,求∠DAC的度数.
图14
21.(9分)如图15,∠ABC和∠BAD的平分线交于点F,BF交AD于点E,∠2+∠3=90°.
(1)求证:BC∥AD;
(2)若∠3=31°,求∠BED的度数.
图15
22.(12分)实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等. 如图16-①,一束光线m射到平面镜l上,被反射后的光线为n,则入射光线m、反射光线n与平面镜l所夹的锐角∠1=∠2.
(1)如图16-②,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=34°,则∠2= ,∠3= ;
(2)请猜想:当两平面镜a,b的夹角∠3= 时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行.并说明理由.
1 ②
图16
附加题(20分,不计入总分)
23.(14分)(1)如图17—①,在△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;
(2)如图17—②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其他条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其他条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论?
图17
第八章 平行线的有关证明综合测评
一、1.B 2.B 3.B 4.A 5.B 6.B 7.C 8.B 9.A
10.A 提示:因为BD⊥FD,所以∠FGD+∠F=90°.因为FH⊥BE,所以∠BGH+∠DBE=90°.因为∠FGD=∠BGH,所以∠DBE=∠F,①正确;因为BE平分∠ABC,所以∠ABE=∠CBE.因为∠BEF=∠CBE+∠C,所以2∠BEF=∠ABC+2∠C.因为∠BAF=∠ABC+∠C,所以2∠BEF=∠BAF+∠C,②正确;因为∠AEB=∠EBC+∠C,∠ABE=∠CBE,所以∠AEB=∠ABE+∠C.因为BD⊥FC,FH⊥BE,所以∠FGD=∠FEB.所以∠BGH=∠ABE+∠C,③正确.所以正确的有3个.
二、11.如果一个三角形是直角三角形 12.118? 13. 72 14.120? 15.①③④
16. 177.5° 提示:先由∠ADC,∠BCD的平分线交于点O1,得出∠O1DC+∠O1CD=(∠ADC+∠DCB),再由∠O1DC,∠O1CD的平分线交于点O2,得出∠O2DC+∠O2CD=(∠ADC+∠DCB),……根据规律可得到∠O6DC+∠O6CD=(∠ADC+∠DCB)=(360°-200°)=2.5°,则∠CO6D=180°-2.5°=177.5°.
三、17. 解:因为∠B=45°,∠C=38°,所以∠DAB=∠B+∠C=45°+38°=83°.
因为∠D=32°,所以∠AFE=∠DAB+∠D=83°+32°=115°.
18.证明:因为∠1=∠C,所以BD∥CE,所以∠2=∠DBE.因为∠3=∠4,所以AD∥BE.所以∠5=∠DBE.所以∠2=∠5.
19.解:(1)假命题,如含有根号,但不是无理数,所以是假命题.
(2)假命题,如a=2,b=7,c=3,满足a+b=2+7=9>3=c, 但它们不能构成三角形,所以是假命题.
(3)真命题.
(4)假命题,如|-3|=|3|,但-3≠3,所以是假命题.
20.解:设∠DAC=x?,则∠1=(63-x)?.
因为∠1=∠2,所以∠2=(63-x)?.
因为∠3是△ABD的一个外角,所以∠3=∠1+∠2=2∠2=2(63-x)? =(126-2x)?.
因为∠4=∠3,所以∠4=(126-2x)?.因为∠BAC+∠2+∠4=180?,所以63+63-x+126-2x=180.解得x=24.所以∠DAC的度数是24 ?.
21.(1)证明:因为AF,BF分别平分∠BAD,∠ABC,所以∠3=∠BAD,∠2=∠ABC.
因为∠2+∠3=90°,所以∠ABC+∠BAD=180°.所以BC∥AD.
(2) 解:因为∠2+∠3=90°,所以∠2=90°-∠3=59°.
因为BF平分∠ABC,所以∠CBE=∠2=59°.
由(1)知BC∥AD,所以∠CBE+∠BED=180°.所以∠BED=180°-∠CBE=121°.
故∠BED的度数为121°.
22.解:(1)68° 90°
提示:因为∠1=∠4=34°,所以∠5=180°-2×34°=112°.
因为m∥n,所以∠2+∠5=180°.所以∠2=68°.
所以∠6=(180°-∠2)=56°.
所以∠3=180°-∠4-∠6=90°.
(2)90°
理由如下:当∠3=90°时,∠4+∠6=90°.
因为∠1=∠4,∠6=∠7,所以∠1+∠7=90°.
所以∠5+∠2=180°-(∠1+∠4)+180°-(∠6+∠7)=360°-(∠1+∠4+∠6+∠7)=180°.
所以m∥n.
23. 解:(1)∠BAC=180°-∠B-∠C=180°-35°-65°=80°.
因为AD平分∠BAC,所以∠BAD=∠BAC=40°.
因为AE⊥BC,所以∠AEB=90°,所以∠BAE=90°-∠B=55°,所以∠DAE=∠BAE-∠BAD=55°-40°=15°.
(2)作AH⊥BC于H,如图②,由(1)得∠DAH=15°.
因为FE⊥BC,所以AH∥EF,所以∠DFE=∠DAH=15°.
(3)作AH⊥BC于点H,如图③,由(1)得∠DAH=15°.
因为FE⊥BC,所以AH∥EF,所以∠DFE=∠DAH=15°.
(4)结合上述三个问题的解决过程,得到∠BAC的平分线所在直线与过角平分线所在直线上的点作BC的垂线之间夹角为15°.
图12
PAGE
第 6 页 共 6 页
第八章 平行线的有关证明综合测评
(本试卷满分100分)
一、选择题(每小题3分,共30分)
1.下列语句中,不是命题的是( )
A.茉莉花是动物 B.过A,B两点作直线
C.两点之间线段最短 D.正数都大于零
2.下列命题:①对顶角相等;②垂直于同一条直线的两直线平行;③两直线平行,同旁内角互补;④同位角相等.其中真命题有( )
A. ①② B. ①③ C. ②④ D. ③④
3.如图,已知∠1=∠2,则能得到AB∥CD的是( )
4.如图1,在△ABC中,点D在AB边上,点E在AC边上,DE∥BC,点B,C,F在一条直线上,若∠A=35?,∠ADE=105?,则∠ACF的度数为( )
A.140? B.135? C.130? D.125?
图1 图2 图3
5.如图2,直线l∥m,将含有45°角的三角尺ABC的直角顶点C放在直线m上,若∠2=18°,则∠1的度数为( )
A. 18? B.27? C.30? D.33?
6.小康放学回家自己煮面条,有下面几道程序:①洗锅盛水2分钟;②洗菜3分钟;③准备面条及佐料2分钟;④用锅把水烧开7分钟;⑤用烧开的水煮面条和菜要3分钟,以上各工序除④外,一次只能进行一道工序,小康要将面条煮好,最少用( )
A.11分钟 B.12分钟 C.13分钟 D.14分钟
7.如图3,下列推理错误的是( )
A.因为∠1=∠3,所以AB∥CD B.因为AB∥CD,所以∠DAB+∠D=180?
C.因为∠DAM=∠CBM,所以AB∥CD D.因为AD∥BC,所以∠2=∠4
8.躺椅为清代出现的具有新样式与功能用途的家具之一,其工艺与技艺随着生活水平的提高而不断升级,标志着人们对生活质量越来越重视,图4是躺椅座驾的侧面示意图,在△ABC中,∠B=45?,∠C=30?,∠EAB=165?,点D在AC上,则△ADE的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
图4 图5
9.如图5,在△ABC中,∠ABC=90°,∠C=24°,D是AC上一点.将△ABC沿BD折叠,使点A落在BC边上的A′处,则∠A′DC的度数为( )
A. 42° B. 40° C. 30° D. 24°
10.如图6,在△ABC中,BD,BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠BGH=∠ABE+∠C.
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
图6
二、填空题(每小题3分,共18分)
11.命题“直角三角形的两锐角互余”的条件是 .
12.如图7,已知AD∥BC,∠1=30?,∠BAC=32?,则∠B=_____.
图7 图8
13.将一条两边互相平行的纸带按图8所示折叠,∠2=36°,则∠1的度数为_______°.
14.如图9-①,“和谐号”高铁列车的小桌板收起来近似看做与地面垂直,展开小桌板使桌面保持水平.图9-②是小桌板展开后的示意图,其中OB表示小桌板桌面的宽度,BC表示小桌板的支架,∠AOB=∠ACB=37?,∠OAC=46?,则∠OBC的度数是______.
1 ②
图9 图10 图11
15.将一副三角尺按图10所示放置,则下列结论:①若∠2=30?,则AC∥DE;②若BC∥AD,则∠2=30?;
③若∠CAD=150?,则∠4=∠C;④∠BAE+∠CAD=180?.其中正确的有_____(填序号).
16. 如图11,在四边形ABCD中,∠A+∠B=200°.作∠ADC,∠BCD的平分线交于点O1,称为第1次操作;作∠O1DC,∠O1CD的平分线交于点O2,称为第2次操作;作∠O2DC,∠O2CD的平分线交于点O3,称为第3次操作;……则第6次操作后∠CO6D的度数是____________.
三、解答题(共52分)
17. (6分)如图12,在△ABC 中,∠B=45°,∠C=38°,E是BC边上一点,ED交CA的延长线于点D,交AB于点F,∠D=32°.求∠AFE的大小.
18.(8分)如图13,已知∠1=∠C,∠3=∠4,求证:∠2=∠5.
图13
19.(8分)下列命题是真命题,还是假命题?如果是假命题,请举出反例.
(1)带根号的数都是无理数;
(2)三条线段a,b,c,若a+b>c,那么这三条线段一定能组成三角形;
(3)同一个平面内,不相交的两条直线一定平行.
(4)若两个数的绝对值相等,那么这两个数一定相等.
20.(9分)如图14,在△ABC中,D是BC边上的点,∠1=∠2,∠3=∠4,∠BAC=63?,求∠DAC的度数.
图14
21.(9分)如图15,∠ABC和∠BAD的平分线交于点F,BF交AD于点E,∠2+∠3=90°.
(1)求证:BC∥AD;
(2)若∠3=31°,求∠BED的度数.
图15
22.(12分)实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等. 如图16-①,一束光线m射到平面镜l上,被反射后的光线为n,则入射光线m、反射光线n与平面镜l所夹的锐角∠1=∠2.
(1)如图16-②,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=34°,则∠2= ,∠3= ;
(2)请猜想:当两平面镜a,b的夹角∠3= 时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行.并说明理由.
1 ②
图16
附加题(20分,不计入总分)
23.(14分)(1)如图17—①,在△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;
(2)如图17—②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其他条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其他条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论?
图17
第八章 平行线的有关证明综合测评
一、1.B 2.B 3.B 4.A 5.B 6.B 7.C 8.B 9.A
10.A 提示:因为BD⊥FD,所以∠FGD+∠F=90°.因为FH⊥BE,所以∠BGH+∠DBE=90°.因为∠FGD=∠BGH,所以∠DBE=∠F,①正确;因为BE平分∠ABC,所以∠ABE=∠CBE.因为∠BEF=∠CBE+∠C,所以2∠BEF=∠ABC+2∠C.因为∠BAF=∠ABC+∠C,所以2∠BEF=∠BAF+∠C,②正确;因为∠AEB=∠EBC+∠C,∠ABE=∠CBE,所以∠AEB=∠ABE+∠C.因为BD⊥FC,FH⊥BE,所以∠FGD=∠FEB.所以∠BGH=∠ABE+∠C,③正确.所以正确的有3个.
二、11.如果一个三角形是直角三角形 12.118? 13. 72 14.120? 15.①③④
16. 177.5° 提示:先由∠ADC,∠BCD的平分线交于点O1,得出∠O1DC+∠O1CD=(∠ADC+∠DCB),再由∠O1DC,∠O1CD的平分线交于点O2,得出∠O2DC+∠O2CD=(∠ADC+∠DCB),……根据规律可得到∠O6DC+∠O6CD=(∠ADC+∠DCB)=(360°-200°)=2.5°,则∠CO6D=180°-2.5°=177.5°.
三、17. 解:因为∠B=45°,∠C=38°,所以∠DAB=∠B+∠C=45°+38°=83°.
因为∠D=32°,所以∠AFE=∠DAB+∠D=83°+32°=115°.
18.证明:因为∠1=∠C,所以BD∥CE,所以∠2=∠DBE.因为∠3=∠4,所以AD∥BE.所以∠5=∠DBE.所以∠2=∠5.
19.解:(1)假命题,如含有根号,但不是无理数,所以是假命题.
(2)假命题,如a=2,b=7,c=3,满足a+b=2+7=9>3=c, 但它们不能构成三角形,所以是假命题.
(3)真命题.
(4)假命题,如|-3|=|3|,但-3≠3,所以是假命题.
20.解:设∠DAC=x?,则∠1=(63-x)?.
因为∠1=∠2,所以∠2=(63-x)?.
因为∠3是△ABD的一个外角,所以∠3=∠1+∠2=2∠2=2(63-x)? =(126-2x)?.
因为∠4=∠3,所以∠4=(126-2x)?.因为∠BAC+∠2+∠4=180?,所以63+63-x+126-2x=180.解得x=24.所以∠DAC的度数是24 ?.
21.(1)证明:因为AF,BF分别平分∠BAD,∠ABC,所以∠3=∠BAD,∠2=∠ABC.
因为∠2+∠3=90°,所以∠ABC+∠BAD=180°.所以BC∥AD.
(2) 解:因为∠2+∠3=90°,所以∠2=90°-∠3=59°.
因为BF平分∠ABC,所以∠CBE=∠2=59°.
由(1)知BC∥AD,所以∠CBE+∠BED=180°.所以∠BED=180°-∠CBE=121°.
故∠BED的度数为121°.
22.解:(1)68° 90°
提示:因为∠1=∠4=34°,所以∠5=180°-2×34°=112°.
因为m∥n,所以∠2+∠5=180°.所以∠2=68°.
所以∠6=(180°-∠2)=56°.
所以∠3=180°-∠4-∠6=90°.
(2)90°
理由如下:当∠3=90°时,∠4+∠6=90°.
因为∠1=∠4,∠6=∠7,所以∠1+∠7=90°.
所以∠5+∠2=180°-(∠1+∠4)+180°-(∠6+∠7)=360°-(∠1+∠4+∠6+∠7)=180°.
所以m∥n.
23. 解:(1)∠BAC=180°-∠B-∠C=180°-35°-65°=80°.
因为AD平分∠BAC,所以∠BAD=∠BAC=40°.
因为AE⊥BC,所以∠AEB=90°,所以∠BAE=90°-∠B=55°,所以∠DAE=∠BAE-∠BAD=55°-40°=15°.
(2)作AH⊥BC于H,如图②,由(1)得∠DAH=15°.
因为FE⊥BC,所以AH∥EF,所以∠DFE=∠DAH=15°.
(3)作AH⊥BC于点H,如图③,由(1)得∠DAH=15°.
因为FE⊥BC,所以AH∥EF,所以∠DFE=∠DAH=15°.
(4)结合上述三个问题的解决过程,得到∠BAC的平分线所在直线与过角平分线所在直线上的点作BC的垂线之间夹角为15°.
图12
PAGE
第 6 页 共 6 页
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
