鲁教版(五四制)六年级下册数学7.3平行线的性质 课件(共30张PPT)
文档属性
| 名称 | 鲁教版(五四制)六年级下册数学7.3平行线的性质 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 486.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-30 11:41:10 | ||
图片预览






文档简介
(共30张PPT)
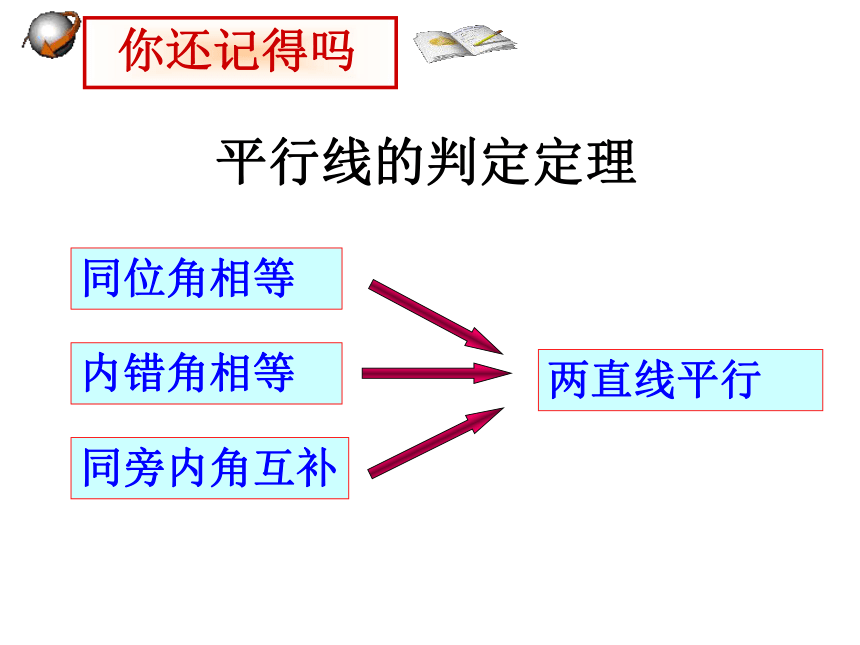
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定定理
想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
角的数量关系
直线的位置关系
如图,
(1)∵ ∠1=____(已知)
∴ a ∥ b ( )
(2)∵ ∠3=____ (已知)
∴ a ∥ b (? )
(3)∵____ +∠3= 180 ° (已知)
∴ a ∥ b ( ??? )
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
c
a
b
1
5
3
4
2
6
∠5
∠5
∠6
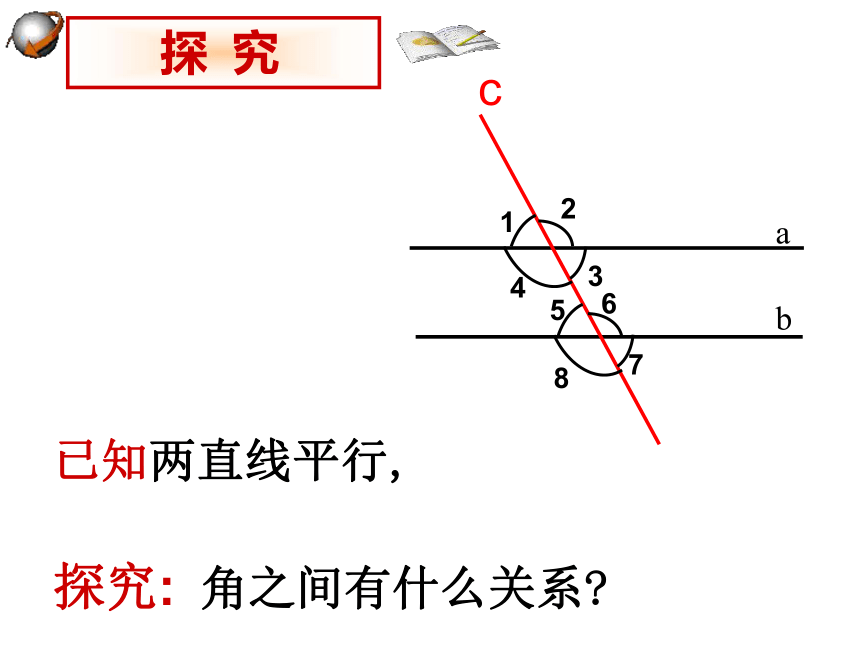
已知两直线平行,
探究: 角之间有什么关系?
a
b
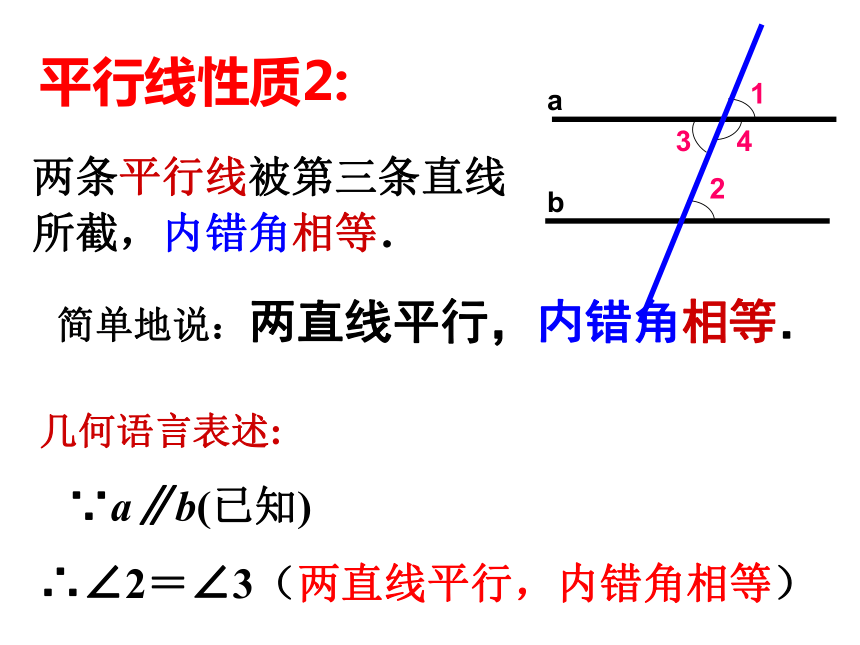
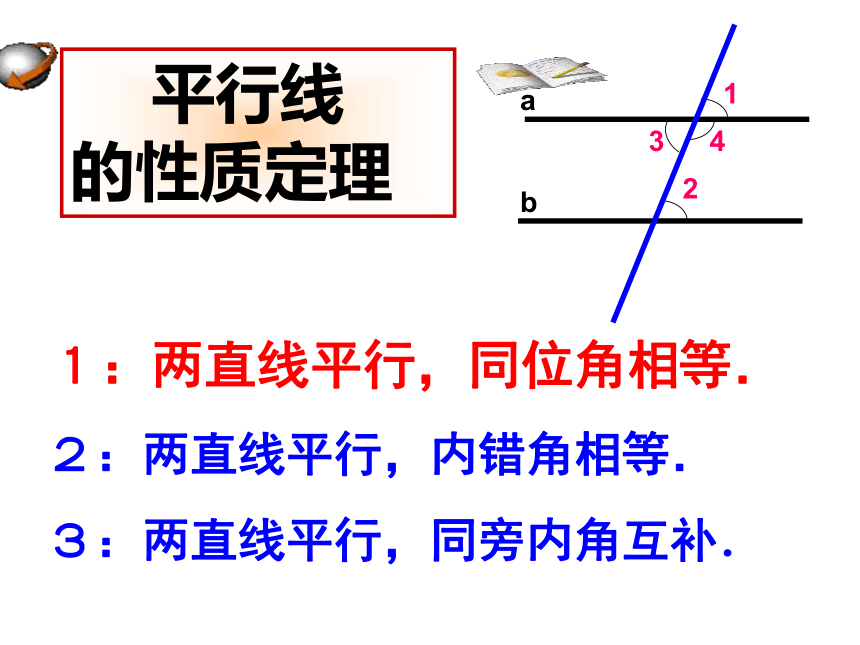
1:两直线平行,同位角相等.
2:两直线平行,内错角相等.
3:两直线平行,同旁内角互补.
简单地说:两直线平行,同位角相等.
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
两条平行线被第三条直线所截,同位角相等.
平行线性质1:
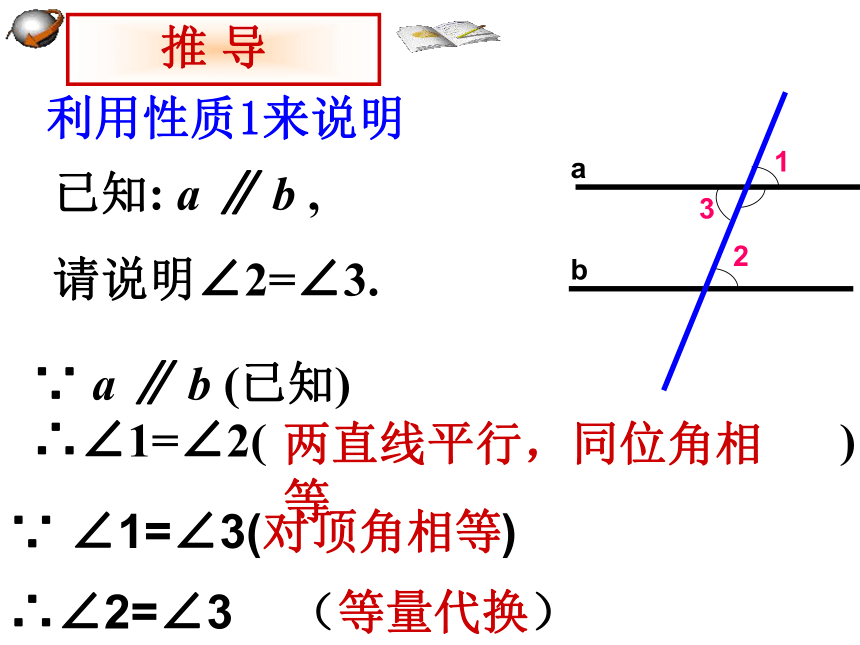
利用性质1来说明
已知: a ∥ b ,
请说明∠2=∠3.
∵ a ∥ b (已知)
∴∠1=∠2( )
∵ ∠1=∠3( )
∴∠2=∠3
两直线平行,同位角相等
对顶角相等
(等量代换)
简单地说:两直线平行,内错角相等.
几何语言表述:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
两条平行线被第三条直线所截,内错角相等.
平行线性质2:
尝试利用性质1来说明
已知: a ∥ b ,
请说明∠2+∠4=180.
简单地说:两直线平行,同旁内角互补。
几何语言表述:
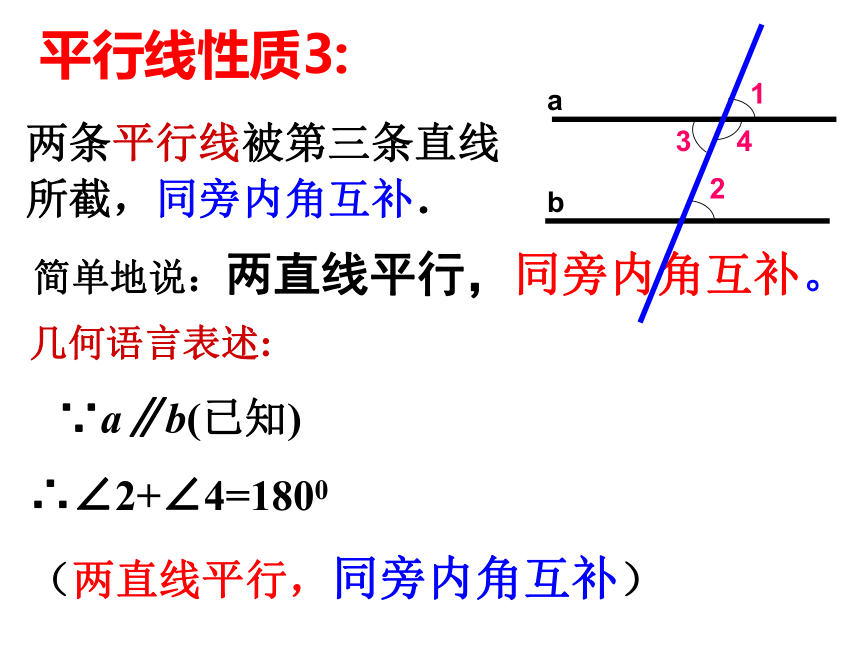
∵a∥b(已知)
∴∠2+∠4=1800
(两直线平行,同旁内角互补)
两条平行线被第三条直线所截,同旁内角互补.
平行线性质3:
1:两直线平行,同位角相等.
2:两直线平行,内错角相等.
3:两直线平行,同旁内角互补.
如图,
(1)∵ a ∥ b (已知)
∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知)
∴ ∠2____∠3 ( )
(3)∵ a ∥ b (已知)
∴ ∠2+∠4=____ ( ??? )
=
两直线平行,同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
c
平行线的判定
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行。
两直线平行,同旁内角互补。
平行线的性质
两直线平行,同位角相等;
两直线平行,内错角相等;
平行线的判定与平行线的性质是因果互换的两类不同的定理,
判定是说:满足了什么条件(性质)的两条直线是互相平行的
性质是说:如果两条直线平行,就应该具有什么性质。
例 如图所示是一块梯形铁片的残余 部分,量得∠A=100?, ∠B=115°,梯形另外两个角各是多少度?
解决问题:
1、如图 ∵AB ∥CD,∴∠1=∠2 (两直线平行,内错角相等 ) ( )
A
B
C
D
2、如图直线 a∥b,则∠1=∠2 .( )
×
×
3、如果有两条直线被第三条直线所截,那么必定有 ( )
(A)内错角相等, (B)同位角相等,(C)同旁内角互补 (D)以上都不对.
D
4、∠1 和∠2是两条直线被第三条直线
所截形成的同旁内角,要使这两条直线平
行,必须 ( )
A. ∠1= ∠2
B. ∠1+∠2=90o
C. 2(∠1+∠2)=360o
D .∠1是钝角, ∠2是锐角
C
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度?为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
B
D
∠4=70o
∵两直线平行,同旁内角互补
2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
∠C=142o
∵两直线平行,内错角相等
3.如图:
∵∠1=∠2( )
∴AD∥ ( )
∴∠BCD+ =180°( )
已知
BC
∠D
内错角相等,两直线平行
两直线平行,同旁内角互补
4.如图1,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
图1
解: ∠A =∠D. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D=____ ( )
∴∠A=∠D ( )
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
5.如图2,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
图2
解: ∠A+∠D=180o. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D+ ____=180o ( )
∴∠A+∠D=180o( )
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
图形
条件
结论
理论依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
平行线的性质
1、配套练习7.5和7.6
2、预习课本P81-P83
1.已知l1∥l2,若∠1与∠2互余,
∠3=120°,求∠4的度数。
150°
课外拓展
2.已知AD∥BC,∠B=55°,
AB平分∠CAD,求∠C的度数。
70°
3、已知:AB∥CD,∠B+∠D=180°, 判断BC与DE的关系?请说明理由。
解:∵DE∥AC( )
∴∠C=__( )
∠3=_____ ( )
又∵DF∥AB( )
∴∠B=__( )
∠A=___ _( )
∴∠A=∠3 ( )
∴∠A+∠B+∠C=∠1+∠2+∠3
=∠BDE=_____
已知
∠1
两直线平行,同位角相等
∠DFC
两直线平行,内错角相等
已知
∠2
两直线平行,同位角相等
∠DFC
两直线平行,同位角相等
等量代换
180°
4、已知:DE∥AC,DF∥AB,
求∠A+∠B+∠C的度数。
5、已知:AB∥CD,
说明∠BED=∠B+∠D
解:∵过点E作EF∥AB
∴∠B=∠1
( )
∵AB∥CD EF∥AB
∴EF∥CD
(
)
如果两直线都与第三条直线平行,那么这两条直线也互相平行
∴∠D=∠2
( )
两直线平行,内错角相等
∴∠BED=∠1+∠2
=∠B+∠D
1
2
两直线平行,内错角相等
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定定理
想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
角的数量关系
直线的位置关系
如图,
(1)∵ ∠1=____(已知)
∴ a ∥ b ( )
(2)∵ ∠3=____ (已知)
∴ a ∥ b (? )
(3)∵____ +∠3= 180 ° (已知)
∴ a ∥ b ( ??? )
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
c
a
b
1
5
3
4
2
6
∠5
∠5
∠6
已知两直线平行,
探究: 角之间有什么关系?
a
b
1:两直线平行,同位角相等.
2:两直线平行,内错角相等.
3:两直线平行,同旁内角互补.
简单地说:两直线平行,同位角相等.
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
两条平行线被第三条直线所截,同位角相等.
平行线性质1:
利用性质1来说明
已知: a ∥ b ,
请说明∠2=∠3.
∵ a ∥ b (已知)
∴∠1=∠2( )
∵ ∠1=∠3( )
∴∠2=∠3
两直线平行,同位角相等
对顶角相等
(等量代换)
简单地说:两直线平行,内错角相等.
几何语言表述:
∵a∥b(已知)
∴∠2=∠3(两直线平行,内错角相等)
两条平行线被第三条直线所截,内错角相等.
平行线性质2:
尝试利用性质1来说明
已知: a ∥ b ,
请说明∠2+∠4=180.
简单地说:两直线平行,同旁内角互补。
几何语言表述:
∵a∥b(已知)
∴∠2+∠4=1800
(两直线平行,同旁内角互补)
两条平行线被第三条直线所截,同旁内角互补.
平行线性质3:
1:两直线平行,同位角相等.
2:两直线平行,内错角相等.
3:两直线平行,同旁内角互补.
如图,
(1)∵ a ∥ b (已知)
∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知)
∴ ∠2____∠3 ( )
(3)∵ a ∥ b (已知)
∴ ∠2+∠4=____ ( ??? )
=
两直线平行,同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
c
平行线的判定
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行。
两直线平行,同旁内角互补。
平行线的性质
两直线平行,同位角相等;
两直线平行,内错角相等;
平行线的判定与平行线的性质是因果互换的两类不同的定理,
判定是说:满足了什么条件(性质)的两条直线是互相平行的
性质是说:如果两条直线平行,就应该具有什么性质。
例 如图所示是一块梯形铁片的残余 部分,量得∠A=100?, ∠B=115°,梯形另外两个角各是多少度?
解决问题:
1、如图 ∵AB ∥CD,∴∠1=∠2 (两直线平行,内错角相等 ) ( )
A
B
C
D
2、如图直线 a∥b,则∠1=∠2 .( )
×
×
3、如果有两条直线被第三条直线所截,那么必定有 ( )
(A)内错角相等, (B)同位角相等,(C)同旁内角互补 (D)以上都不对.
D
4、∠1 和∠2是两条直线被第三条直线
所截形成的同旁内角,要使这两条直线平
行,必须 ( )
A. ∠1= ∠2
B. ∠1+∠2=90o
C. 2(∠1+∠2)=360o
D .∠1是钝角, ∠2是锐角
C
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度?为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
B
D
∠4=70o
∵两直线平行,同旁内角互补
2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
∠C=142o
∵两直线平行,内错角相等
3.如图:
∵∠1=∠2( )
∴AD∥ ( )
∴∠BCD+ =180°( )
已知
BC
∠D
内错角相等,两直线平行
两直线平行,同旁内角互补
4.如图1,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
图1
解: ∠A =∠D. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D=____ ( )
∴∠A=∠D ( )
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
5.如图2,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
图2
解: ∠A+∠D=180o. 理由:
∵ AB∥DE( )
∴∠A=____ ( )
∵AC∥DF( )
∴∠D+ ____=180o ( )
∴∠A+∠D=180o( )
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
图形
条件
结论
理论依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
平行线的性质
1、配套练习7.5和7.6
2、预习课本P81-P83
1.已知l1∥l2,若∠1与∠2互余,
∠3=120°,求∠4的度数。
150°
课外拓展
2.已知AD∥BC,∠B=55°,
AB平分∠CAD,求∠C的度数。
70°
3、已知:AB∥CD,∠B+∠D=180°, 判断BC与DE的关系?请说明理由。
解:∵DE∥AC( )
∴∠C=__( )
∠3=_____ ( )
又∵DF∥AB( )
∴∠B=__( )
∠A=___ _( )
∴∠A=∠3 ( )
∴∠A+∠B+∠C=∠1+∠2+∠3
=∠BDE=_____
已知
∠1
两直线平行,同位角相等
∠DFC
两直线平行,内错角相等
已知
∠2
两直线平行,同位角相等
∠DFC
两直线平行,同位角相等
等量代换
180°
4、已知:DE∥AC,DF∥AB,
求∠A+∠B+∠C的度数。
5、已知:AB∥CD,
说明∠BED=∠B+∠D
解:∵过点E作EF∥AB
∴∠B=∠1
( )
∵AB∥CD EF∥AB
∴EF∥CD
(
)
如果两直线都与第三条直线平行,那么这两条直线也互相平行
∴∠D=∠2
( )
两直线平行,内错角相等
∴∠BED=∠1+∠2
=∠B+∠D
1
2
两直线平行,内错角相等
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
