人教版七年级数学 下册5.3.1 平行线的性质 课时练(含答案)
文档属性
| 名称 | 人教版七年级数学 下册5.3.1 平行线的性质 课时练(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 106.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-30 10:17:47 | ||
图片预览

文档简介
第五章 相交线与平行线
5.3.1 平行线的性质
一、选择题
1、如图1所示,DE∥BC,DF∥AC,下列结论正确的个数为( )
①∠C=∠AED ②∠EDF=∠BFD ③∠A=∠BDF ④∠AED=∠DFB
A.1个 B.2个 C.3个 D.4个
2、如图2所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有( )
A.2个 B.3个 C.4个 D.5个
3、如图3,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )
A.65° B.55° C.45° D.35°
4、如图,,那么∠1.∠2.∠3的关系是( )
A.∠1+∠2+∠3=360° B.∠1+∠2-∠3=180°
C.∠1-∠2+∠3=180° D.∠1+∠2+∠3=180°
5、如图,已知AB∥CD,EA是∠CEB的平分线,若∠BED=40°,则∠A的度数是( )
A.40° B.50° C.70° D.80°
填空题
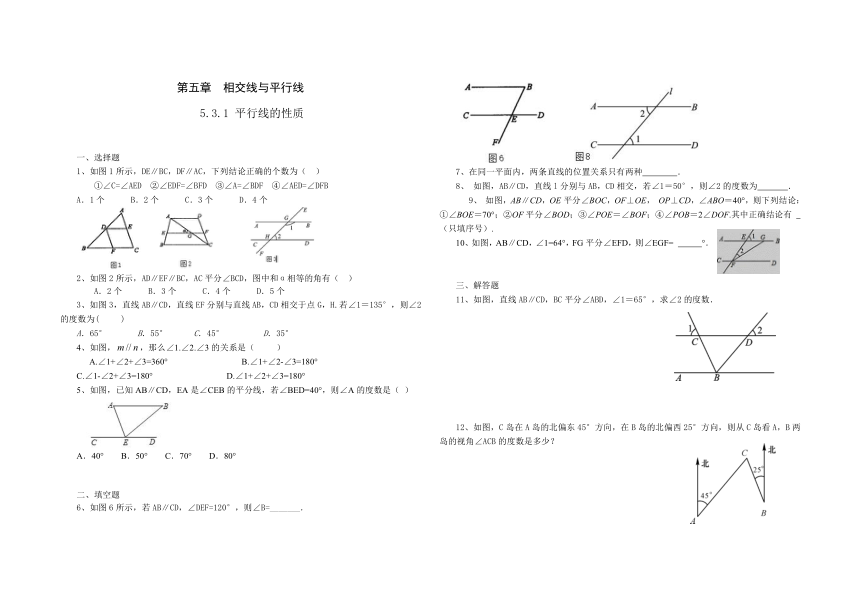
6、如图6所示,若AB∥CD,∠DEF=120°,则∠B=_______.
7、在同一平面内,两条直线的位置关系只有两种 .
8、 如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为 .
9、 如图,AB∥CD,OE平分∠BOC,OF⊥OE, OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有 (只填序号).
10、如图,AB∥CD,∠1=64°,FG平分∠EFD,则∠EGF= ? °.
三、解答题
11、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
12、如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则从C岛看A,B两岛的视角∠ACB的度数是多少?
13、如图,已知EAB是直线,AD∥BC,AD平分∠EAC,试判定∠B与∠C的大小关系,并说明理由.
14、如图,点A在直线MN上,且MN//BC.求证:∠BAC+∠B+∠C=180°.
M A N
B C
15、如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
16、已知:如图,D,F,E分别是BC,AC,AB上的点,DF∥AB,DE∥AC,
试说明∠EDF=∠A.
17、如图,已知AD∥BE,∠A=∠E,求证:∠1=∠2.
18、如图,已知∠B=∠C,AD∥BC,求证:AD平分∠CAE.
19、阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
参考答案:
一、1、D(点拨:∵DE∥BC,∴∠C=∠AED,∠EDF=∠BFD,∵DF∥AC,∴∠A=∠BDF,∵DE∥BC,DF∥AC,∴∠AED=∠DFB.) 2、C(点拨:∠FGC=∠FCA=∠BCA=∠DAC) 3、C 4、B 5、C
二、6、60°
7、相交,平行
8、50°
9、①②③
10、32
三、11、解:∵直线AB∥CD,∠1=65°,
∴∠ABC=∠1=65°.
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°.
∵直线AB∥CD,∴∠ABD+∠BDC=180°.
∴∠2=∠BDC=180°-∠ABD=180°-130°=50°.
12、70°
13、解:∠B=∠C.
理由:∵AD平分∠EAC,∴∠EAD=∠DAC.
∵AD∥BC,∴∠EAD=∠B,∠DAC=∠C.
∴∠B=∠C.
14、证明:∵MN∥BC,∴∠B=∠MAB,∠C=∠NAC.
∵∠BAC+∠MAB+∠NAC=180°,∴∠BAC+∠B+∠C=180°.
15、解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°.∴∠DCF=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
16、解:∵DF∥AB(已知),
∴∠A+∠AFD=180°(两直线平行,同旁内角互补).
∵DE∥AC(已知),
∴∠AFD+∠EDF=180°(两直线平行,同旁内角互补).
∴∠A=∠EDF(同角的补角相等).
17、证明:∵AD∥BE,
∴∠A=∠EBC.
∵∠A=∠E,
∴∠EBC=∠E.
∴DE∥AB.
∴∠1=∠2.
18、证明:∵AD∥BC,∴∠2=∠B,∠1=∠C.
∵∠B=∠C,∴∠1=∠2,∴AD平分∠CAE.
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
19、解:如图乙,过点P作PE∥AB.
∵AB∥CD(已知),
∴PE∥AB∥CD(平行于同一直线的两条直线平行).
∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等).
∵∠APC=∠EPA+∠EPC,
∴∠APC=∠A+∠C(等量代换).
如图丙,过点P作PF∥AB.
∴∠FPA=∠A(两直线平行,内错角相等).
∵AB∥CD(已知),
∴PF∥CD(平行于同一直线的两条直线平行).
∴∠FPC=∠C(两直线平行,内错角相等).
∵∠FPC-∠FPA=∠APC,
∴∠C-∠A=∠APC(等量代换).
5.3.1 平行线的性质
一、选择题
1、如图1所示,DE∥BC,DF∥AC,下列结论正确的个数为( )
①∠C=∠AED ②∠EDF=∠BFD ③∠A=∠BDF ④∠AED=∠DFB
A.1个 B.2个 C.3个 D.4个
2、如图2所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有( )
A.2个 B.3个 C.4个 D.5个
3、如图3,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )
A.65° B.55° C.45° D.35°
4、如图,,那么∠1.∠2.∠3的关系是( )
A.∠1+∠2+∠3=360° B.∠1+∠2-∠3=180°
C.∠1-∠2+∠3=180° D.∠1+∠2+∠3=180°
5、如图,已知AB∥CD,EA是∠CEB的平分线,若∠BED=40°,则∠A的度数是( )
A.40° B.50° C.70° D.80°
填空题
6、如图6所示,若AB∥CD,∠DEF=120°,则∠B=_______.
7、在同一平面内,两条直线的位置关系只有两种 .
8、 如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为 .
9、 如图,AB∥CD,OE平分∠BOC,OF⊥OE, OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有 (只填序号).
10、如图,AB∥CD,∠1=64°,FG平分∠EFD,则∠EGF= ? °.
三、解答题
11、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
12、如图,C岛在A岛的北偏东45°方向,在B岛的北偏西25°方向,则从C岛看A,B两岛的视角∠ACB的度数是多少?
13、如图,已知EAB是直线,AD∥BC,AD平分∠EAC,试判定∠B与∠C的大小关系,并说明理由.
14、如图,点A在直线MN上,且MN//BC.求证:∠BAC+∠B+∠C=180°.
M A N
B C
15、如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
16、已知:如图,D,F,E分别是BC,AC,AB上的点,DF∥AB,DE∥AC,
试说明∠EDF=∠A.
17、如图,已知AD∥BE,∠A=∠E,求证:∠1=∠2.
18、如图,已知∠B=∠C,AD∥BC,求证:AD平分∠CAE.
19、阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
参考答案:
一、1、D(点拨:∵DE∥BC,∴∠C=∠AED,∠EDF=∠BFD,∵DF∥AC,∴∠A=∠BDF,∵DE∥BC,DF∥AC,∴∠AED=∠DFB.) 2、C(点拨:∠FGC=∠FCA=∠BCA=∠DAC) 3、C 4、B 5、C
二、6、60°
7、相交,平行
8、50°
9、①②③
10、32
三、11、解:∵直线AB∥CD,∠1=65°,
∴∠ABC=∠1=65°.
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°.
∵直线AB∥CD,∴∠ABD+∠BDC=180°.
∴∠2=∠BDC=180°-∠ABD=180°-130°=50°.
12、70°
13、解:∠B=∠C.
理由:∵AD平分∠EAC,∴∠EAD=∠DAC.
∵AD∥BC,∴∠EAD=∠B,∠DAC=∠C.
∴∠B=∠C.
14、证明:∵MN∥BC,∴∠B=∠MAB,∠C=∠NAC.
∵∠BAC+∠MAB+∠NAC=180°,∴∠BAC+∠B+∠C=180°.
15、解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°.∴∠DCF=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
16、解:∵DF∥AB(已知),
∴∠A+∠AFD=180°(两直线平行,同旁内角互补).
∵DE∥AC(已知),
∴∠AFD+∠EDF=180°(两直线平行,同旁内角互补).
∴∠A=∠EDF(同角的补角相等).
17、证明:∵AD∥BE,
∴∠A=∠EBC.
∵∠A=∠E,
∴∠EBC=∠E.
∴DE∥AB.
∴∠1=∠2.
18、证明:∵AD∥BC,∴∠2=∠B,∠1=∠C.
∵∠B=∠C,∴∠1=∠2,∴AD平分∠CAE.
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
19、解:如图乙,过点P作PE∥AB.
∵AB∥CD(已知),
∴PE∥AB∥CD(平行于同一直线的两条直线平行).
∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等).
∵∠APC=∠EPA+∠EPC,
∴∠APC=∠A+∠C(等量代换).
如图丙,过点P作PF∥AB.
∴∠FPA=∠A(两直线平行,内错角相等).
∵AB∥CD(已知),
∴PF∥CD(平行于同一直线的两条直线平行).
∴∠FPC=∠C(两直线平行,内错角相等).
∵∠FPC-∠FPA=∠APC,
∴∠C-∠A=∠APC(等量代换).
