沪科版八年级物理《10.1、杠杆平衡条件》同步例题与试题以及答案
文档属性
| 名称 | 沪科版八年级物理《10.1、杠杆平衡条件》同步例题与试题以及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-02 22:28:31 | ||
图片预览


文档简介
《§10.1、科学探究:杠杠的平衡条件》同步提升策略
班级 姓名
【夯实基础——预习导学知识点梳理】
一、杠杆:1.定义:在力的作用下,能绕某一 转动的硬棒(直棒或曲棒)。这个固定点叫 。
2、动力作用线:沿动力的方向所画的直线——有时需要沿动力示意图的方向正向或反向延长(用虚线表示)
阻力作用线:沿阻力的方向所画的直线——有时需要沿阻力示意图的方向正向或反向延长(用虚线表示)3.杠杆五要素:(画力臂——“模型法”的又一应用)
支点: ;用符号 表示;
⑵动力: 杠杆转动的力,用符号 表示;
⑶阻力: 杠杆转动的力,用符号 表示;
⑷动力臂:从 到 的距离,用符号 表示
⑸阻力臂:从 到 的距离,用符号 表示。
4.杠杆的平衡条件:用文字可表示为 。(即:阿基米德发现的杠杆原理)
⑴杠杆平衡条件的数学表达式,乘积式: . 从乘积式可以看出:杠杆平衡条件是比较“力与力臂的乘积FL”是否相等,而不是单独比较“力的大小F” 或“力臂大小L” 是否相等。
⑵杠杆平衡条件的数学表达式,比例式: 。 从比例式可以看出:加在杠杆上的力和它的力臂成反比,即动力与动力臂成 ;阻力与阻力臂成 (以上两空均选填:“正比”或“反比”)。 ⑶作用在杠杆上的动力为50N,阻力为600N,杠杆恰好平衡,则杠杆的动力臂和阻力臂之比为 。
5.分类:⑴省力杠杆:动力臂 阻力臂的杠杆。特点是省力,但费 。例如:撬棒、核桃钳
⑵费力杠杆:动力臂 阻力臂的杠杆。特点是费力,但省 。例如:镊子、筷子
⑶等臂杠杆:动力臂 阻力臂的杠杆。特点是既不省力,也不省距离。例如:托盘天平
⑷有没有既省力又省距离的杠杆?答 。
6、同“光线”和“力的示意图”,用力臂(虚线)表示支点到力的作用线的距离体现出的方法是 法。
7、当力的作用线通过支点时,力臂的大小为 。
8、一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力,欲使其一端抬离地面。则C
A.F甲>F乙,因为甲方法的动力臂长
B.F甲C.F甲>F乙,因为乙方法时阻力臂短
D.F甲=F乙,因为动力臂都是阻力臂的2倍
9、示工具中,使用时不能省力但能省距离的是D
专题一:杠杆的五要素及其作图
【典型例题】:
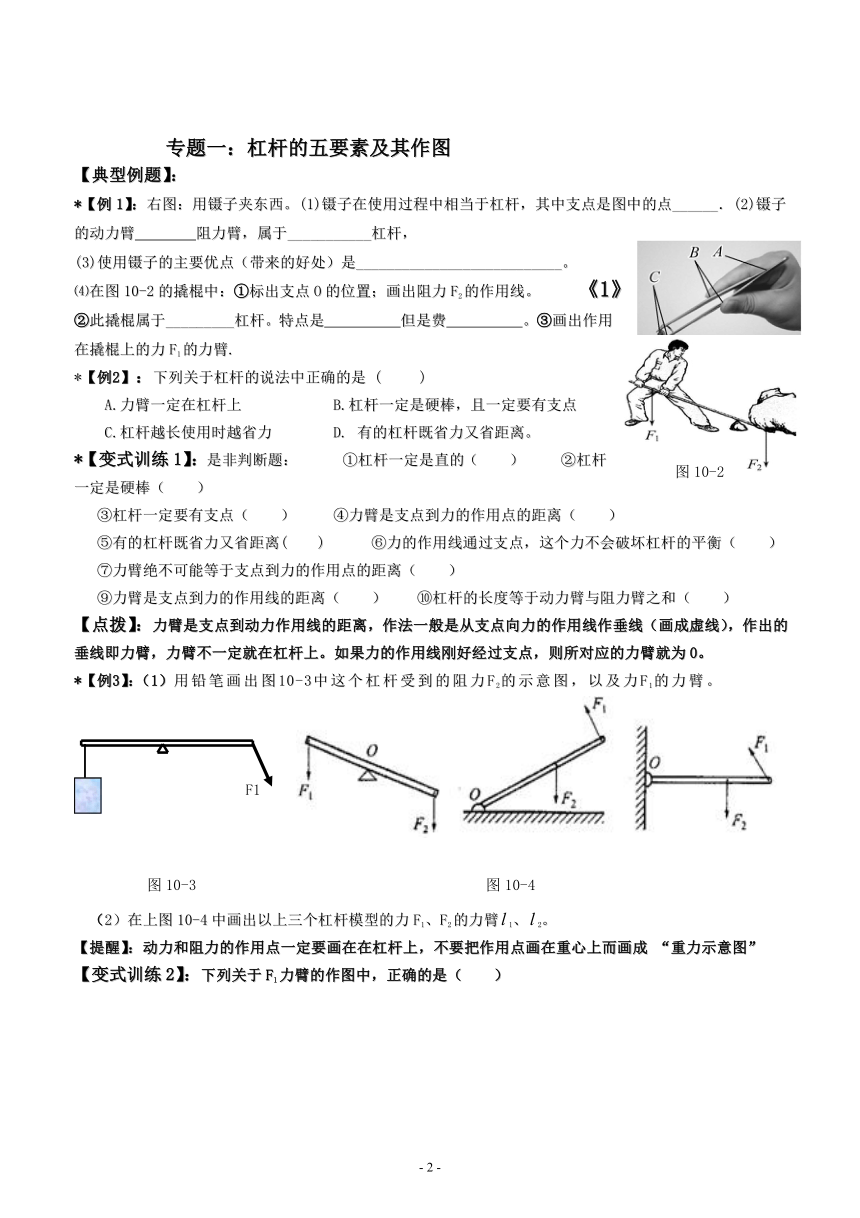
*【例1】:右图:用镊子夹东西。(1)镊子在使用过程中相当于杠杆,其中支点是图中的点______.(2)镊子的动力臂 阻力臂,属于___________杠杆,
(3)使用镊子的主要优点(带来的好处)是___________________________。
⑷在图10-2的撬棍中:①标出支点O的位置;画出阻力F2的作用线。 《1》
②此撬棍属于_________杠杆。特点是 但是费 。③画出作用在撬棍上的力F1的力臂.
*【例2】:下列关于杠杆的说法中正确的是 ( )
A.力臂一定在杠杆上 B.杠杆一定是硬棒,且一定要有支点
C.杠杆越长使用时越省力 D. 有的杠杆既省力又省距离。
*【变式训练1】:是非判断题: ①杠杆一定是直的( ) ②杠杆一定是硬棒( )
③杠杆一定要有支点( ) ④力臂是支点到力的作用点的距离( )
⑤有的杠杆既省力又省距离( ) ⑥力的作用线通过支点,这个力不会破坏杠杆的平衡( )
⑦力臂绝不可能等于支点到力的作用点的距离( )
⑨力臂是支点到力的作用线的距离( ) ⑩杠杆的长度等于动力臂与阻力臂之和( )
【点拨】:力臂是支点到动力作用线的距离,作法一般是从支点向力的作用线作垂线(画成虚线),作出的垂线即力臂,力臂不一定就在杠杆上。如果力的作用线刚好经过支点,则所对应的力臂就为0。
*【例3】:(1)用铅笔画出图10-3中这个杠杆受到的阻力F2的示意图,以及力F1的力臂。
(2)在上图10-4中画出以上三个杠杆模型的力F1、F2的力臂?
?1、2。
【提醒】:动力和阻力的作用点一定要画在在杠杆上,不要把作用点画在重心上而画成 “重力示意图”
【变式训练2】:下列关于F1力臂的作图中,正确的是( )
【点拨】:如何正确的画出力臂:一找支点、二画线、三连距离、四标签。即分为以下4步:
⑴支点O;⑵画力的作用线(虚线);⑶画力臂(虚线,过支点垂直力的作用线作垂线);⑷标力臂(大括号)
*【例4】:如下图10-6:先在图中做出此杠杆的五要素,然后用字母符号在对应的位置标出杠杆的五要素:支点用符号 表示;动力用符号 表示;动力臂用符号 表示;阻力用符号 表示; 阻力臂用符号 表示。杠杆平衡条件的数学表达式 :乘积式: . 比例式: .
;
【变式训练3】:铡刀在使用时的受力情况如图10-7所示,某学生在图中分别作出了F1和F2的力臂L1和L2,其中 的作法不对。(选填“L1”、“L2”、“L1和 L2”)
【解析】:读图可知,动力的力臂L不是从“支点”到动力作用线的距离,而是从 “物体的中心”到动力作用线的距离,因此不符合力臂的要求.图中重新标注部分才是动力的力臂.
【例5】:如果把铁锨看作是费力杠杆,在图10-8中所示的A、B、C三点中,支点是 点,动力作用点是 点,阻力作用点是 点。
【解析】:在铁锨的使用中,人的左手用力下压,而右手用力上抬,使铁锨抬起来。由此可见,人的左手充当支点,右手给杠杆提供动力,铁锨上的重物对铁锨的压力就是铁锨向上的阻力。所以,A点是阻力作用点,B点是动力作用点,C点是支点。
*【例6】:如图10-9所示,请画出杠杆在图示位置静止时作用在A点的最小动力F及其力臂。
【解析】:作图原理:力和它的力臂成反比,所以动力臂最长时对应的动力最小。又根据动力与动力臂垂直,因此:从动力的作用点做动力臂的垂线,即为最小动力。
以此题为例: 作最小动力的方法步骤:①第一步:找到离支点最远的点为动力作用点A;②第二步:连接支点O和动力作用点A,即为最长的动力臂;③第三步:在A点作动力臂的垂线——带剪头的垂线。即为最小的动力(力的方向不要画反)。
#【变式训练4】:一直径是100厘米、重量是400牛顿的均匀圆桶放在水平地面上,并靠在高10厘米的台阶边,如右图所示。小明要在圆柱体边缘最小施多大的力才能使圆桶滚上
台阶?画出这个力。 解:
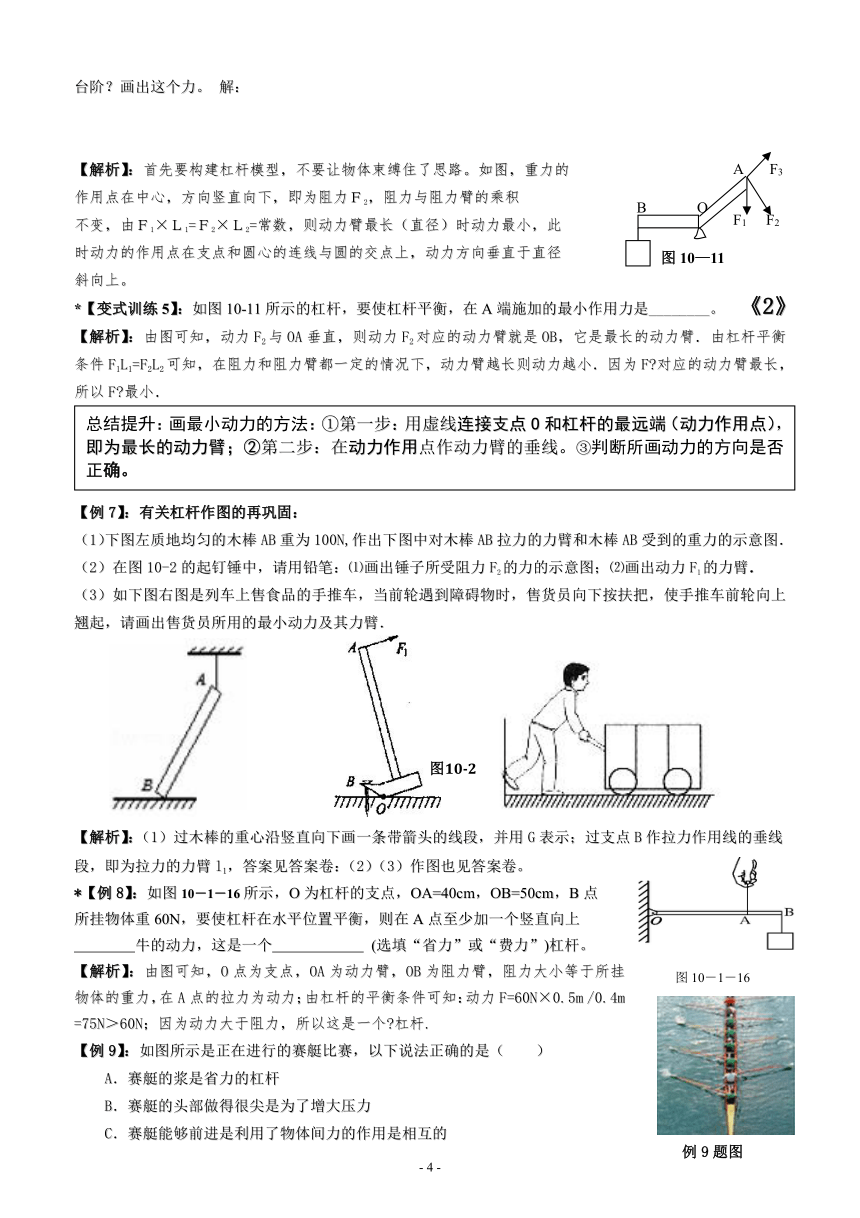
【解析】:首先要构建杠杆模型,不要让物体束缚住了思路。如图,重力的
作用点在中心,方向竖直向下,即为阻力F2,阻力与阻力臂的乘积
不变,由F1×L1=F2×L2=常数,则动力臂最长(直径)时动力最小,此
时动力的作用点在支点和圆心的连线与圆的交点上,动力方向垂直于直径
斜向上。
*【变式训练5】:如图10-11所示的杠杆,要使杠杆平衡,在A端施加的最小作用力是________。 《2》
【解析】:由图可知,动力F2与OA垂直,则动力F (?http:?/??/?www.21cnjy.com?)2对应的动力臂就是OB,它是最长的动力臂.由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小.因为F?对应的动力臂最长,所以F?最小.
【例7】:有关杠杆作图的再巩固:
(1)下图左质地均匀的木棒AB重为100N,作出下图中对木棒AB拉力的力臂和木棒AB受到的重力的示意图.
(2)在图10-2的起钉锤中,请用铅笔:⑴画出锤子所受阻力F2的力的示意图;⑵画出动力F1的力臂.
(3)如下图右图是列车上售食品的手推车,当前轮遇到障碍物时,售货员向下按扶把,使手推车前轮向上翘起,请画出售货员所用的最小动力及其力臂.
【解析】:(1)过木棒的重心沿竖直向下画一条带箭头的线段,并用G表示;过支点B作拉力作用线的垂线段,即为拉力的力臂l1,答案见答案卷:(2)(3)作图也见答案卷。
*【例8】:如图10-1-16所示,O为杠杆的支点,OA=40cm,OB=50cm,B点
所挂物体重60N,要使杠杆在水平位置平衡,则在A点至少加一个竖直向上
牛的动力,这是一个 (选填“省力”或“费力”)杠杆。
【解析】:由图可知,O点为支点,OA为动力臂,OB为阻力臂,阻力大小等于所挂物体的重力,在A点的拉力为动力;由杠杆的平衡条件可知:动力F=60N×0.5m /0.4m =75N>60N;因为动力大于阻力,所以这是一个?杠杆.
【例9】:如图所示是正在进行的赛艇比赛,以下说法正确的是( )
A.赛艇的浆是省力的杠杆
B.赛艇的头部做得很尖是为了增大压力
C.赛艇能够前进是利用了物体间力的作用是相互的
D.赛艇能漂浮在水面上是由于它所受的浮力大于重力
【解析】:A、赛艇的桨在使用过程中,动力臂小于阻力臂,是费力杠杆,省距离,故A错误;
B、赛艇的头部做得很尖是为了减小水的阻力,故B错误;
C、当赛艇前进时,赛艇的桨给水一个向后的力,因为物体间力的作用是相互的,水就会对桨产生一个向前的力,使赛艇前进,故C正确; D、因为赛艇漂浮在水面上,所以F浮=G总,故D错误; 故选
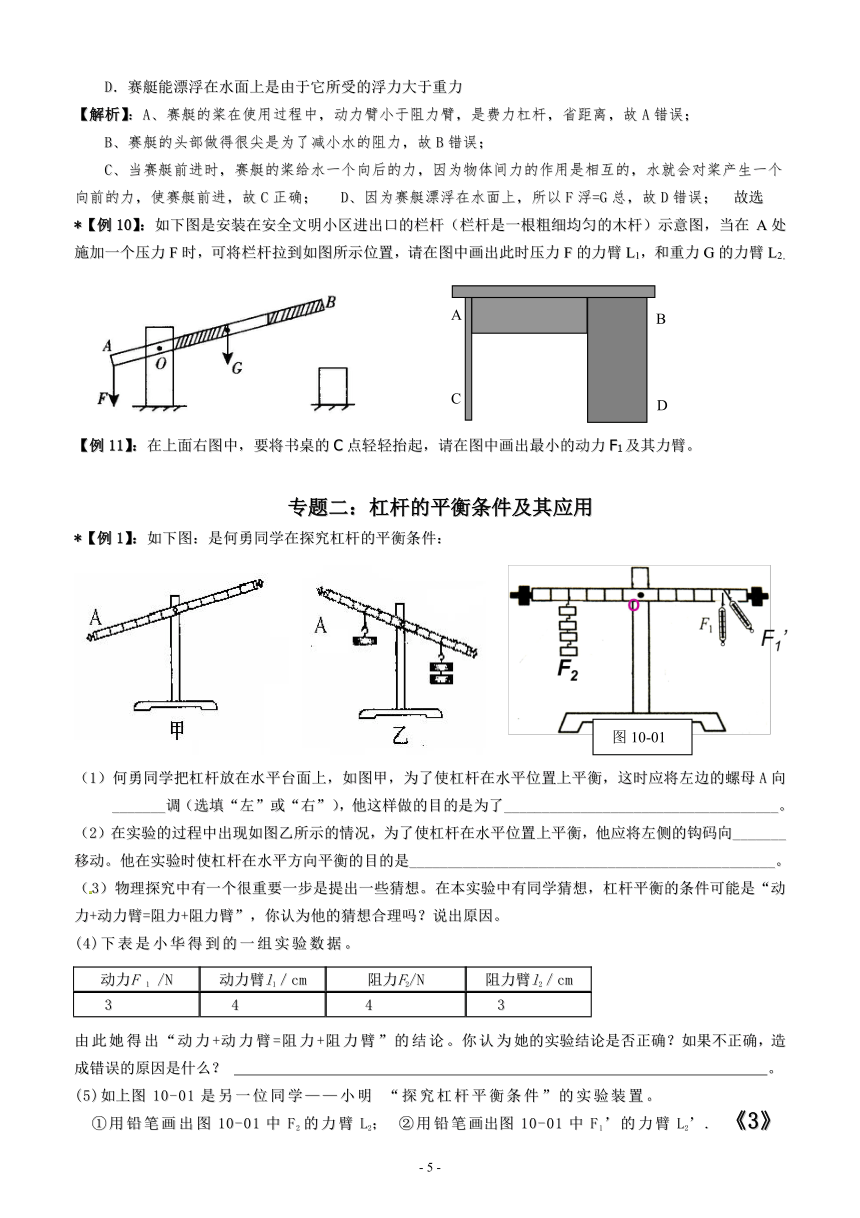
*【例10】:如下图是安装在安全文明小区进出口的栏杆(栏杆是一根粗细均匀的木杆)示意图,当在 A处施加一个压力F时,可将栏杆拉到如图所示位置,请在图中画出此时压力F的力臂L1,和重力G的力臂L2。
【例11】:在上面右图中,要将书桌的C点轻轻抬起,请在图中画出最小的动力F1及其力臂。
专题二:杠杆的平衡条件及其应用
*【例1】:如下图:是何勇同学在探究杠杆的平衡条件:
(1)何勇同学把杠杆放在水平台面上,如图甲,为了使杠杆在水平位置上平衡,这时应将左边的螺母A向_______调(选填“左”或“右”),他这样做的目的是为了____________________________________。
(2)在实验的过程中出现如图乙所示的情况,为了使杠杆在水平位置上平衡,他应将左侧的钩码向_______移动。他在实验时使杠杆在水平方向平衡的目的是________________________________________________。
(3)物理探究中有一个很重要一步是提出一些猜想。在本实验中有同学猜想,杠杆平衡的条件可能是“动力+动力臂=阻力+阻力臂”,你认为他的猜想合理吗?说出原因。
(4)下表是小华得到的一组实验数据。
动力F 1 /N 动力臂l1/cm 阻力F2/N 阻力臂l2/cm
3 4 4 3
由此她得出“动力+动力臂=阻力+阻力臂”的结论。你认为她的实验结论是否正确?如果不正确,造成错误的原因是什么? 。
(5)如上图10-01是另一位同学——小明 “探究杠杆平衡条件”的实验装置。
①用铅笔画出图10-01中F2的力臂L2; ②用铅笔画出图10-01中F1’的力臂L2’. 《3》
(6)每个钩码均重0.5N,如图10-01所示,在杠杆右侧改为用弹簧测力计竖 (?http:?/??/?www.21cnjy.com?)直向下拉,此时弹簧测力计示数为F1,当弹簧测力计逐渐向右倾斜处于F1’的位置时,使杠杆仍然在水平位置平衡,则弹簧测力计的示数为
F1’则 F1 F1’(选填:大于、小于、等于),其原因是F1’的力臂要比F1的力臂 。
(7)本实验得出杠杆的平衡条件是:_____________________。
【解析】:在探究杠杆平衡条件时,两次使杠杆平衡,一次是实验前,调节平衡螺母,使杠杆在水平位置平衡,这样是为了消除杠杆自重对实验结果的影响和便于测量力臂;第二次是在实验过程中,调节钩码的个数和位置,使杠杆再次在水平位置平衡,这是为了便于测出杠杆的力臂。(7)F1L1=F2L2
【解答】:(1)右 消除杠杆自重对实验结果的影响(或:便于测量力臂) (2)左的钩码向左移(或把右边的钩码向左移;或减少右边的钩码数量等) 便于测出杠杆的力臂 (3)不合理。力和力臂是不同的物理量,不能相加。 (4)不正确,一次实验得出实验结论具有偶然性,得多做几次实验。(5)①②作图略; (6) 根据“力和它的力臂成反比”,当弹簧测力计逐渐向右倾斜时,F1’的力臂变小,对应的拉力就增大。
【点拨】:在探究杠杆平衡条件的实验中要“两次”使杠杆在水平方向平衡,第一次是实验前,调节平衡螺母;第二次是调节钩码的位置,使杠杆在水平方向平衡。
【变式训练1】:在做研究杠杆平衡的条件实验时,小红根据如图10-1-7甲所示的实验现象得出的杠杆平衡条件是:“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”。为了说明这一结论并不正确,请你在图乙所示的杠杠上画出需要对杠杠施加的力的示意图和这个力的力臂。
【解析】:在A点或者B点沿不同方向拉弹簧测力计,使杠杆在水平位置平衡。现象是:力的方向改变,力的大小也发生改变。动力×支点到动力作用点的距离≠阻力×支点到阻力作用点的距离,但是却始终满足动力×动力臂=阻力×阻力臂。作图参看答案。
【例2】:如图10-1-8所示,质量可忽略的杠杆上所标的每一格长度都是相等的,O为支点,杠杆两边所挂的每一个钩码均相同,杠杆在水平位置平衡。在下列情况下,杠杆仍在水平位置保持平衡的是( )
A.两边都减少一个钩码 B.两边的钩码下各加挂一个相同的钩码
C.左边钩码向右移一格,右边钩码同时向左移一格
D.右边钩码下加挂一个相同的钩码,左边钩码同时向左移一格
【解析】:图中左边:力×力臂=2×3 = 6,右边:力×力臂=3×2 = 6,杠杆在水平位置平衡。A中两边都减少一个钩码,左边:力×力臂=1×3 = 3,右边:力×力臂=2×2 = 4,杠杆不平衡,右端下降。A选项错。同理,我们可分析出B、C选项错。D选项中,左边:钩码同时向左移一格后,力×力臂= 4×2 = 8,右边:加挂一个相同的钩码后,力×力臂= 4×2 = 8,杠杆可以继续在水平位置保持平衡。所以选?
*【变式训练2】:如图6-5-3所示,挂着的各个钩码质量相等,杠杆处于平衡状态,当两边钩码下各增加1个同样的钩码时( ) A.杠杆左端下降 B.杠杆右端下降
C.杠杆仍然平衡 D.无法判断
【解析】:杠杆平衡的条件是:“左右两侧力和力臂的成绩相等”。
【解答】:增加钩码前,杠杆平衡,则有2G·3L=3G·2L(设每个钩码重为G,每段杆长都为L),左右两边都增加一个钩码,左边力和力臂的乘积变为3G·3L,右边力和力臂的乘积变为4G·2L。因为左边力和力臂的乘积>右边力和力臂的乘积变,所以杠杆左端下降。
#【变式训练3】:不等臂直杠杆在动力和阻力作用下,已经处于平衡状态,采用下列办法不能使杠杆平衡的是 ( ) A.在杠杆上再施加一个力,使这个力的作用线通过杠杆的中点,但不通过支点
B.在杠杆上再施加一个力,使这个力的作用线通过支点
C.使动力和阻力同时减小到原来的1/2 D.使动力臂和阻力臂同时变为原来的2倍
【解析】:杠杆平衡条件是动力×动力臂 = 阻力×阻力臂,不论改变力还是改变力臂,只要满足杠杆的平衡条件,则杠杆仍然平衡。沿力的方向画的一条直线称为力的作用线,在杠杆上施力,但这个力的作用线通过杠杆的支点,则这个力的力臂为零,不影响杠杆的平衡。在杠杆上再施加一个力,使这个力的作用线通过杠杆的中点,但不通过支点,所加的这个力不能满足动力×动力臂 = 阻力×阻力臂,则这个力不能使杠杆平衡
【例3】:如图10-1-10所示,用一根木 (?http:?/??/?www.21cnjy.com?)棒撬大石头,没有撬动,为了撬动大石头,应将垫在木棒下的小石块向 移动,这实质上是增大了 ,同时又减小了 。
【解析】:小石块向左移,增大了动力臂,同 (?http:?/??/?www.21cnjy.com?)时又减小了阻力臂.在动力和阻力
不变的情况下,动力和动力臂的乘积才会大于阻力和阻力臂的乘积,才会撬动
大石头.故答案为:
【变式训练4】:如图10-1-11,杆秤是民间的一种测量工具。使用时,将待
测物体挂在秤钩A上,用手拎住秤钮B或C(相当于支点),秤砣D在秤杆E上
移动,当杆秤水平平衡时就可以在秤杆上读出读数。
(1)从科学的角度来看,杆秤应该是一种测量 大小的工具。
(2)根据杠杆平衡的条件分析,使用杆秤时,当从秤纽C换到秤纽B时,
杆秤的测量值将变 。
【解析】:杆秤是用来测量物体质量的一种测量工具,是杠杆的应用。根据杠杆
平衡条件F1L1 = F2L2可知,被测物体离称钮越近,即力臂越短,被测物体的质量就越大。所以当从秤纽C换到秤纽B时,杆秤的测量值将变大。
*【例4】:如图6-5-4所示,下列器件中属于费力杠杆的是( ) 《4》
(?http:?/??/?www.21cnjy.com?/??)
【解析】:根据杠杆平衡条件,省力杠杆是动力臂大于阻力臂的杠杆。瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆.核桃夹子在使用过程中,动力臂大于阻力臂,是省力杠杆.钳子在使用过程中,动力臂大于阻力臂,是省力杠杆.镊子在使用过程中,动力臂小于阻力臂,是费力杠杆.故答案为?
【变式训练5】:如下图所示的工具中,正常使用时属于省力杠杆的是( )
【解析】:根据杠杆平衡条件,动力臂大于阻力臂的杠杆为省力杠杆;动力臂小于阻力臂的杠杆为费力杠杆;坩埚钳由于动力臂小于阻力臂是费力杠杆;筷子夹菜时由于动力臂小于阻力臂是费力杠杆;镊子夹取物体时,动力臂小于阻力臂是费力杠杆;B图为剪铁皮的剪刀,其动力臂大于阻力臂,是省力杠杆。 故答案为。
【例5】:如图是吊车起吊贷物的结构示意图,伸缩撑杆为圆弧状,工作时它对吊臂的支持力始终与吊臂垂直,使吊臂绕O点缓慢转动,从而将货物提起
.下列说法正确的是( )
A. 吊臂是一省力杠杆,但要费距离
B. 吊臂是一个费力杠杆,但可以省功
C. 匀速顶起吊臂的过程中,伸缩撑杆支持力的力臂变小
D. 匀速顶起吊臂的过程中,伸缩撑杆支持力渐渐变小
【解析】:由图可知,伸缩撑杆的阻力臂大于动力臂,所以吊臂是一个费力杠杆,A错误;机械可以省距离,但不能省功,B错误;伸缩撑杆为圆弧状,伸缩时对吊臂的支持力始终与吊臂垂直.则动力臂保持不变,在伸缩撑杆匀速顶起吊臂的过程中,重物的阻力臂逐渐减小.由杠杆的平衡条件可知伸缩撑杆受到支持力渐渐变小。
【例6】:如下图所示是安置在巴中大佛寺收费站栏杆的示意图,当在A处施加一个动力时,可将栏杆拉起来,它是一根( ) A.省力杠杆 B.费力杠杆 C.等臂杠杆 D.无法确定
【解析】:从支点到动力作用线的距离叫做动力臂;从支点到阻力作用线的距离叫做阻力臂.动力臂大于阻力臂的杠杆为省力杠杆;动力臂小于阻力臂的杠杆为费力杠杆;由图可知杠杆绕A点右侧的轴转动,A点右侧的轴为支点,则作用在A点的动力的力臂远远大于杠杆重力的阻力臂,所以此栏杆是一个费力杠杆.选?.
【知识点补充】:
生活中的“省力杠杆”:撬棍、羊角锤、瓶盖起子、老虎钳、起子(开瓶器)、手推车、剪铁皮和修剪树枝的剪刀、杆秤、动滑轮、道钉撬、裁衣剪刀、指甲刀、核桃夹、自行车刹车闸等。
生活中的“费力杠杆”:筷子、镊子、钓鱼竿、脚踏板、扫帚、船桨、理发剪刀、起重机(起重臂),人手臂(胳膊),食品夹子、缝纫机的踏板等
【等臂杠杆】:天平、定滑轮,(跷跷板?)
*【变式训练6】:图6-5-23所示是一个指甲刀的示意图,它由三个杠杆ABC、OBD和OED组成,用指甲刀剪指甲时,下面说法正确的是( )
A.三个杠杆都是省力杠杆 B.三个杠杆都是费力杠杆
C.ABC是省力杠杆,OBD、OED是费力杠杆
D.ABC是费力杠杆,OBD、OED是省力杠杆
【解析】:指甲剪可以看成是由一个撬棒和一个镊子组成:
①撬棒是ABC,以B为支点,动力作用在A上,阻力作用在C上,使用时动力臂大于阻力臂,是省力杠杆;
②镊子是由OBD和OED两个杠杆组成,支点O点,动力作用在E点,阻力作用在D点.使用时动力臂小于阻力臂,是费力杠杆.故答案为
【友情点拨】:对于类似的实际中使用的杠杆,要善于从实际的工具中抽象出具体的杠杆模型。在确定杠杆的几个要素时,要抓住研究对象是杠杆,在确定杠杆的支点时,可以设想让被研究的工具动一动,在动的过程中,便可确定固定不动的点,即支点;再结合杠杆平衡条件来分析杠杆的省力或费力情况。
*【例7】:如图所示,杠杆AOB用细线悬挂起来,分别在A、B两端分别挂上质量为m1、m2的重物时,杠杆平衡,此时AO恰好处于水平位置,AO=BO,不计杠杆重力,则m1、m2的关系为( )
A.m1>m2 B.m1<m2 C.m1=m2 D.无法判断
例7题图 图10-1-8 例8题图
【解析】:根据杠杆的平衡条件:F1L1=F2L2可知,G1L1=G2L2,m1gL1=m2gL2,即m1L1=m2L2,力与相应的力臂成反比关系,从图中可以看出力臂L1>L2,所以物体的重力G1<G2,那么质量m1 m2的大小关系可知。
【变式训练7】:如上图10-1-8所示,A点的弹簧测力计无论是竖直向下还是倾斜向下都可以使杠杆平衡,由杠杆的平衡条件可知( )
A.倾斜拉动,弹簧测力计的示数较大 B.竖直拉动,弹簧测力计的示数较大
C.两种方法弹簧测力计的示数相等 D.无论弹簧测力计怎样拉动,弹簧测力计的示数都小于物重
【解析】:力臂是支点到力的作用线的距离,竖直向下拉弹簧的力臂(5格长)最大且大于左端拉力力臂(3格长),此时拉力小于物重且最小;倾斜拉,完全有可能出现弹簧拉力力臂大于、等于、小于左边的拉力力臂,所以弹簧拉力会有小于、等于、大于物重的可能性. 《5》
*【例8】:如图所示,杠杆的支点O,在A端加一个动力(图中未画出),使杠杆在水平位置平衡,则杠杆( ).
A.一定省力 B.一定费力 C.不省力也不费力 D.以上三种情况均有可能
【解析】:如图所示的杠杆,在水平位置平衡,阻力作用在B处,所以阻力臂是一定的,即OB;动力作用在A端,当动力方向竖直向上时,动力臂最长是OA,OA大于OB,是省力杠杆,能省力;若动力方向不是竖直向上时,动力臂一定小于OA,但有可能大于OB,此时,也是省力杠杆,能省力。动力臂也有可能等于阻力臂OB,即动力臂等于阻力臂,是等臂杠杆,既不省距离也不省力;动力臂也有可能小于阻力臂OB,即动力臂小于阻力臂,是费力杠杆,费力但省距离。故此杠杆也可能省力,也可能费力,也可能不省力也不费力。故选?
【变式训练8】:请你仔细观察如右图所示的漫画,究竟小猴和小兔谁分的萝卜重?简要说明理由。
答:
【解析】:参看《同步学习》68页第8题。此题中小猴和小羊在分萝卜时利用了杠杆的平衡,用支点使萝卜处于水平位置的平衡。表面看来兔子要的那头多或者有人认为两边一样多,但是实际上就像小猴所说兔子中计了,小猴拿的那个比较重。根据杠杆的平衡条件,在杠杆平衡的条件下,力臂越大则力越小,而小猴那块的重心离支点近,力臂小;小兔那块重心离支点远,力臂大。所以小猴那块要比小兔那块重。
*【例9】:如图10-13所示,作用在杠杆一端且始终与杠杆垂直的力F,将杠杆缓慢地由位置A拉至位置B。在这个过程中,动力F_________(选填“变大”、“变小”或“不变”)
图10-13 图10-14
【解析】:根据杠杆平衡的条件,当杠杆的力臂发生变化时,相对应的力也会跟着变化。在研究杠杆变化的问题时,还要用到控制变量的方法。在本题中不变的物理量为阻力G和动力臂l1,阻力臂在变化,所以动力也随之变化。 【解答】:由题意可知,阻力G和动力臂l1没有发生变化(如上图所示),在提升时阻力臂l2变大,根据杠杆平衡条件Fl1=Gl2,动力F在变大。
*#【变式训练9】:如上图10-14所示杠杆,力F方向始终竖直向上,当此杠杆在动力F作用下,将一个由细绳系的物体由图中位置逆时针匀速转动到水平位置时,则 ( )
A.F大小始终不变? B.F变大? C.F先变小后变大 D.无法判断F大小的变化
【解析】:根据相似三角形,动力臂和阻力臂的比值不变,等于支点到力的作用点的长度之比,阻力不变,所以动力F始终不变。如图乙所示画出杠杆的力臂,在提升重物时,阻力臂l2在变小,动力臂l1也在变小。但可以把杠杆平衡的条件写成杠杆的比例式:F1/F2=L2/L1,其中F2=G物,利用数学上的相似三角形可知,在提升时,L2/L1的大小是不变的,F2(G物)没有变化,所以提力F1的大小?
【变式训练10】:如下图甲所示,刘刚同学在利用一根扁担抬起一个水桶,她用一个始终向上的力把这个水桶提离地面。他把水桶抬离地面一个较小的高度的过程中,提力F________。(填“变大”“变小”“不变”)
【变式训练9】图甲 【变式训练9】图乙 【例10】题图
【解析】:思路点拨:分析杠杆在变化时,要首先明确杠杆要素中哪些要素在变。如图乙所示画出杠杆的力臂,在提升水桶时,阻力臂l2在变小,动力臂l1也在变小,所以无法直接判断F的大小如何变化。但可以把杠杆平衡的条件变化为比例式,我们能否比较的大小如何变化呢?利用数学上的相似三角形可以知道,当在提升时,L2/L1的大小是不变的,阻力G没有变化,所以提力F的大小?
【例10】:某同学做探究杠杆平衡条件的实验.(1)实验时,为了方便对力臂的测量 (?http:?/??/?www.21cnjy.com?),该同学先调节平衡螺母,使杠杆在 位置平衡;这是为了便于 。并通过多次实验才能总结出杠杆的平衡条件,多次试验的目的是为了排除实验的 ,寻找普遍规律.
(2)实验中,在杠杆上的A点挂四个重均为 (?http:?/??/?www.21cnjy.com?)0.5N的钩码,用调好的弹簧测力计竖直向上拉杠杆上的B点,使杠杆水平平衡,如上图右图所示,测力计的示数是 N;如果将测力计沿图中虚线方向拉,仍使杠杆在水平位置平衡,则测力计的示数将 (变大/不变/变小).
【解析】:(1)答案为:水平;测量力臂;偶然性。(2)弹簧测力计竖直向上拉杠杆时,动力臂是OB,当弹簧测力计倾斜拉杠杆时,阻力和阻力臂不变,但因为动力和动力臂成反比。当动力臂减小时,动力就会变大.
【例11】:将重为80牛的物体挂在1.8米长的杠杆一端,在另一端加上16牛的动力
时杠杆平衡,则动力臂与阻力臂之比为 (提示:用杠杆平衡条件的“比例式”
求解更简单);动力臂长为 米。
【解析】:杠杆平衡条件的比例式:L1 /L2=F2 /F1可以求出动力臂与阻力臂之比L1 /L2=F2 /F1=80 /16=?再将L2=1.8- L1, F1=16N, F2=G=80N,代入杠杆平衡条件公式F1L1=F2L2,可以求出动力臂L1。
【变式训练11】:如右图2是一种拉杆式旅行箱的示意图,使用时相当于一个 力
(填“省”或“费”)力杠杆;若箱和物品共重100N,动力臂是阻力臂的5倍,则抬起拉杆的力至少为 N。
【例12】:小明在学校参加植树活动时,使用如图10-1-4所示的钢丝钳,剪铁丝固定小树苗。
(1)他使用的钳子是省力杠杆还是费力杠杆?(2)在图中画出动力F1的力臂L1
和作用在这根杠杆上的阻力F2。 (3)剪铁丝时动力臂长为10cm,阻力臂长为2cm,若铁丝被剪断需要1000N的力,小明至少用多大的力才能将铁丝剪断?
解:
6》
专题三:综合提升练
【例1】:如下图10-16杠杆在力F1 ,F2作用下处于平衡状态,L1为F1的力臂。请在图中作出F2的力臂L2及力Fl。
【解析】:过L1的端点做垂直于L1的垂线,与杠杆的交点即为动力作用点,为使杠杆平衡,方向向上;
从支点到F2作用线的距离即为L2,过L2的端点做垂直于L1的垂线,就是力Fl。 答案见答案卷
图10-16 图10-17 图10-18
【变式训练11】:如图10-17,杠杆OA在力F1、F2的作用下静止,l2是F2的力臂,画出F1的力臂和力F2
【解析】:类同【例1】的解析。
【例2】:如图10-18所示,在“研究杠杆平衡条件”的实验中共有5个相同的钩码供选择,杠杆上每格距离相等,先将杠杆在水平位置调节平衡后,在杠杆左边离支点O三格的A处挂了2个钩码。为使杠杆的水平位置平衡,如果只在支点右边挂钩码,请你回答所挂钩码的位置和钩码的个数: (只回答一种方法即可)。
【例3】:一根重100牛顿的均匀直铁棒放在水平地面上,抬起一端所需最小的力是( )
A.50牛顿. B.75牛顿. C.25牛顿. D.100牛顿.
【解答】:需要50N 。因为它的重心在中点处 我们的力施加在一端。这样 动力臂和阻力臂之比是2:1, 所以动力与阻力之比是1:2,因为力和它的力臂成反比:F1/F2=L2/L1;抬起一端所需最小的力是。
【例4】:如图6-5-13所示,用撬棒撬一块大石头,已知棒AB=0.7m、BC=0.2m、CD=0.1m,撬棒在C 处受到石头的压力为2000N,欲撬动石头,所用的力必须大于多少?(棒的自重不计)要求:用两种方法并通过具体计算,判断得出结果。
【解析】:撬棒在使用过程中,作用在A点上的动力F即可向上也可向下、或其它方向,但因题目要求用两种方法求解,且每种方法均要求所用的力要最小,所以作用在A点的力必须与杆AB垂直。
解答:(1)若作用在A点的力沿斜下方且与杆AB垂直,则杆将绕着B(支)点转动,根据杠杆的平衡条件F1L1=F2L2可知,此时杠杆的动力臂L1=AB=0.7m,阻力臂L2=BC=0.2m,欲撬动石头,作用在杠杆A点上的最小力应为
(2)若作用在A点的力沿斜上方且与杆AB垂直,则杆将绕着D(支)点转动,根据杠杆的平衡条件F1L1=F2L2可知,此时杠杆的动力臂L1=AD=0.7m+0.2m+0.1m=1m,阻力臂L2=BC=0.1m,欲撬动石头,作用在杠杆A点上的最小力应为:
【例5】:小柯积极参加体育锻炼.如图所示为 (?http:?/??/?www.21cnjy.com?)他在练习俯卧撑.此时他的身体可看为一个杠杆,O点是支点.他的重力为600N,所受重力可视为集中在A点.将身体撑起时,(1)地面对双手的支持力至少多大?(2)若每个手掌的面积为0.02m2,双手对地面的压强有多大?
【解析】:(1)将人体视为杠杆,支持力F的力臂为L1=1.2m;重力G的力臂L2为0.8m;
由杠杆的平衡条件得:FL1=GL2,即F×1.2m=600N×0.8m;则F=400N,地面对双手的支持力至少为?N.
(2)解答:力的作用是相互的∴双手对地面的压力等于支持力:F压=F1=300N;再根据压强公式(定义式)
两个手掌的总面积为0.02m2×2=0.04,m2 。将压力和受力面积代入压强公式 P=F/S即可求出压强。
解:
【例6】:如图所示,秤砣的质量 (?http:?/??/?www.21cnjy.com?)为100g,秤杆的质量忽略不计.秤杆水平静止时,OA=5cm,OB=25cm,则被测物的质量为 kg.若秤砣有缺损时,则杆秤所示的质量值 (填“偏大”或“偏小”).
【变式训练12】:已知物体在月球上的重力大约是地球上重力的六分之一。做生意时,用同一杆秤在月球上称质量,和在地球上相比( )
A. 买方吃亏 B. 卖方吃亏 C. 双方都不吃亏 D. 双方都吃亏
【解析】:到月球上后,动力臂和阻力臂都不变,而动力和阻力都变为原来的1/6,所以杠杆依旧平衡,所以
【例7】:两个质量相等的实心的铜球和铁球(ρ铜>ρ铁),分别挂在杠杆的两端,杠杆平衡。现将两球同时浸没在水中,杠杆( ) A.不平衡,挂铜球一端下降 B.不平衡,挂铁球一端下降
C.仍然平衡 D.无法判断
【解析】:受力分析一下:铜球和铁球两个质量相等,G铜=G铁。同时浸没在水中,因为ρ铜>ρ铁,m铜=m铁,所以V铜小于V铁G ,F浮铁> F浮铜,铁块受到的竖直向上的浮力大,所以挂铜球一端下降。 A
#【例8】:如下图10-1-7所示,一根粗细均匀的硬棒AB被悬挂起来,已知AB=6AO,当在A处悬挂一重为100牛的重物时,杠杆恰好平衡,杠杆自身的重力多大。
#【例9】:如图10-1-9所示,一支均匀的直尺放在水平桌面上,一端
伸出桌面,已知伸出桌面的部分是全尺的三分之一。当在B端挂一个5N重物时,
直尺的A端刚刚开始翘起,则此木尺的重力是______N。
#【例10】:如图10-1-10所示,直径为36cm的半球形碗固定在水平面上,碗的端口水平。一根密度分布均匀、长度为47cm的光滑杆ABC搁置在半球碗上,碗的厚度不计,杆平衡时碗内部分AB段与碗外部分BC段的长度之比为(? ?) 《7》
A.38:9 B.35:12 C.32:15 D.27:20
#【例11】:如图8所示,AO=40厘米,BO=20厘米,拉力F=3牛,并与水平
方向成30°角。若在木棒B端悬挂体积为100厘米3的物体G,并将它浸没在
水中,木棒恰好平衡,则物体的重力应为多大?
【同步跟踪练习】
1.如图10-1-11所示,杠杆调平衡后,在A处挂3个钩 (?http:?/??/?www.21cnjy.com?)码,要想杠杆继续平衡,则需在B处挂 个钩码.杠杆在水平位置平衡后,两侧各去掉一个钩码,则杠杆的 端将上升.(每个钩码的质量都相同)
解答:(1)由题意可知,杠杆在水平位置平衡,设一个钩码的重力为G,一个格为L,由杠杆平衡条件可知,3G×5L=nG×3L,解得:n=5;所以在杠杆右边B处应挂5个够码. (2)如果A、B两处各去掉一个钩码,左边:2G×5L=10GL,右边:4G×3L=12GL,所以左端小于右端,右端下降,左端将上升. 故答案为
2.用杠杆撬起一块重1000N的石块,如果动力臂长100cm,阻力臂长10cm,那么用_____N的力就可以了.
3、如图10-1-12所示,B端悬挂一重为G的重物,不计杠杆自重,在A点施加动力F使杠杆保持水平平衡.则下列说法正确的是( ?)
A.当杠杆平衡时,一定满足G×OB=F×OA
B.因为OA大于OB,所以F小于G
C.杠杆可能为等臂杠杆 D.动力的方向一定竖直向下
4、如图所示,杠杆的左端悬挂着一个重物,右端用弹簧测力计拉着,使
杠杆在水平方向保持平衡。若将弹簧测力计缓慢地沿着图中虚线自位置1
移到位置2,并保持杠杆始终在水平方向平衡,则弹簧测力计的示数变化是( )
A.不断增大 B.不断减小 C.先增大,然后减小 D.先减小,然后增大
【思路点拨】:判断拉力的变化,就要分析拉力的力臂如何变化。在本题中弹簧测力计由1位置拉到2位置过程中,力臂是先变大后变小的,当拉力方向与杠杆垂直时力臂最大。
《§10.1、科学探究:杠杠的平衡条件》同步提升策略 《参考答案》
专题一:杠杆的五要素及其作图。
【典型例题】:【例1】:答案略。 【例2】:B。 【变式训练1】:②③⑥⑨是正确的,其它错。
【例3】:答案略。 【变式训练2】:C。 【例4】答案见10—1—1。 【变式训练3】:L1。
【例5】:C;B;A。 【例6】:见下图10—1—2。 【变式训练4】:见图10—1—2。L2=30厘米(50厘米的平方和40厘米的平方的开方)由F1×L1=F2×L2 得F1=F2×L2/L1=400N×30cm/100cm=120N。所以,小明要将圆柱体滚上台阶所需的最小作用力为120N。 【变式训练5】:F2。 【例7】:见图10-1-4的三幅图。 【例8】:75,费力。 【例9】:C。 【例10】:图10-1-5。 【例11】:见图10-1-6。
专题二:杠平衡条件及其应用
【例1】:【解答】:(1)右 消除杠杆自重对实验结果的影响 (2)左的钩码向左移(或把右边的钩码向左移;或减少右边的钩码数量等) 便于测出杠杆的力臂 (3)不合理。力和力臂是不同的物理量,单位不同,不能相加。(4)不正确,一次实验得出实验结论具有偶然性,得多做几次实验。(5)①②作图略;
③“<”;(6) “小于”,“短”。 (7)F1L1=F2L2
【变式训练1】:见图10-1-7。 【例2】:D。【变式训练2】:A。 【变式训练3】:A。【例3】:左,动力臂,阻力臂. 【变式训练4】:(1)质量 (2)大。 【例4】:D。 【变式训练5】:B。 【例5】:D。 【例6】:A。 【变式训练6】:C. 【例7】:B。 【变式训练7】:A。 【例8】:D。 【变式训练8】:小猴分得的萝卜重,如图所示,萝卜平衡时,粗的那端力臂短,根据杠杆平衡条件,粗的那端萝卜更重。
【例9】:变大。 【变式训练9】:A。 【变式训练10】:不变。 【例10】:(1)答案为:水平;测量力臂;偶然性。(2)变大。 【例11】:5:1;1.5. 【变式训练11】:省;20N。
【例12】:(1)省力杠杆;(2)图略。(3)解:根据杠杆平衡条件 ,可得
专题三:综合提升练
【例1】:图10-1-10。 【变式训练11】:见下图10-1-11。 【例2】:在两格出挂3个钩码。
【例3】:50牛
【例4】:(1) (2)
[答案] 两次所用的力分别为571N和200N。
【例5】:力的作用是相互的∴双手对地面的压力等于支持力:F压=F1=300N;
【例6】: 解:如图10-1-12所示: 因为杠杆平衡,所以G1LOA=G2LOB,
即:m1gLOA=m2gLOB,则m1===500g=0.5kg.
若秤砣有缺损,m2减小,而G1LOA不变,所以LOB要变大,杆秤所示的质量值要偏大.故答案为:0.5;偏大.
【变式训练12】:C。【例7】:A。【例8】:50N 【例9】:50N。 【例10】:C。 【例11】:B。
图10-1
图10-2
F1
图10-3 图10-4
图10-1 图10-1
图10-2 图10-3
L1
F1
F1
O
A
F1
L1
D
L1
C
F1
O
L1
B
图10-6 图10-7 图10-8
总结提升:力臂的画法:一找点,二划线,三作垂线段,四把力臂现(标力臂)。
A
图10-9
训练4图101010-10
B
O
A
F3
F1
图10—11
F2
总结提升:画最小动力的方法:①第一步:用虚线连接支点O和杠杆的最远端(动力作用点),即为最长的动力臂;②第二步:在动力作用点作动力臂的垂线。③判断所画动力的方向是否正确。
④根据动力和阻力使杠杆转动的方向相反,
图10-2
图10-1-16
例9题图
A
B
C
D
图10-01
甲
乙 22222
图10-1-7
总结提升:为什么要调节杠杆在水平位置平衡?如何调节?实验时为什么要做多次实验、收集多组数据?
实验前,先调节______________,使杠杆在水平位置平衡,这样做的好处是________________________
图10-1-8
图6-5-3
总结提升:判断一个杠杆在两个力的作用下是否处于平衡状态,是比较“两个力和各自力臂的乘积是否相等”,而不是单纯比较“力的大小” 或“力臂大小”。
图10-1-10
图10-1-11
D.镊子
图6-5-23
图 10-1-4
图6-5-13
图10-1-7
O
图10—1—9
图10-1-10
图10-1-11
图10-1-12
图10-1-12
10—1—3
F1
F2
图10-1-5
图10-1-1
F1
F2
A
图10-1-2
图10-1-4
图10-1-11
图10-1-12
10-1-6
F
10-1-7
10-1-10
1
11
班级 姓名
【夯实基础——预习导学知识点梳理】
一、杠杆:1.定义:在力的作用下,能绕某一 转动的硬棒(直棒或曲棒)。这个固定点叫 。
2、动力作用线:沿动力的方向所画的直线——有时需要沿动力示意图的方向正向或反向延长(用虚线表示)
阻力作用线:沿阻力的方向所画的直线——有时需要沿阻力示意图的方向正向或反向延长(用虚线表示)3.杠杆五要素:(画力臂——“模型法”的又一应用)
支点: ;用符号 表示;
⑵动力: 杠杆转动的力,用符号 表示;
⑶阻力: 杠杆转动的力,用符号 表示;
⑷动力臂:从 到 的距离,用符号 表示
⑸阻力臂:从 到 的距离,用符号 表示。
4.杠杆的平衡条件:用文字可表示为 。(即:阿基米德发现的杠杆原理)
⑴杠杆平衡条件的数学表达式,乘积式: . 从乘积式可以看出:杠杆平衡条件是比较“力与力臂的乘积FL”是否相等,而不是单独比较“力的大小F” 或“力臂大小L” 是否相等。
⑵杠杆平衡条件的数学表达式,比例式: 。 从比例式可以看出:加在杠杆上的力和它的力臂成反比,即动力与动力臂成 ;阻力与阻力臂成 (以上两空均选填:“正比”或“反比”)。 ⑶作用在杠杆上的动力为50N,阻力为600N,杠杆恰好平衡,则杠杆的动力臂和阻力臂之比为 。
5.分类:⑴省力杠杆:动力臂 阻力臂的杠杆。特点是省力,但费 。例如:撬棒、核桃钳
⑵费力杠杆:动力臂 阻力臂的杠杆。特点是费力,但省 。例如:镊子、筷子
⑶等臂杠杆:动力臂 阻力臂的杠杆。特点是既不省力,也不省距离。例如:托盘天平
⑷有没有既省力又省距离的杠杆?答 。
6、同“光线”和“力的示意图”,用力臂(虚线)表示支点到力的作用线的距离体现出的方法是 法。
7、当力的作用线通过支点时,力臂的大小为 。
8、一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力,欲使其一端抬离地面。则C
A.F甲>F乙,因为甲方法的动力臂长
B.F甲
D.F甲=F乙,因为动力臂都是阻力臂的2倍
9、示工具中,使用时不能省力但能省距离的是D
专题一:杠杆的五要素及其作图
【典型例题】:
*【例1】:右图:用镊子夹东西。(1)镊子在使用过程中相当于杠杆,其中支点是图中的点______.(2)镊子的动力臂 阻力臂,属于___________杠杆,
(3)使用镊子的主要优点(带来的好处)是___________________________。
⑷在图10-2的撬棍中:①标出支点O的位置;画出阻力F2的作用线。 《1》
②此撬棍属于_________杠杆。特点是 但是费 。③画出作用在撬棍上的力F1的力臂.
*【例2】:下列关于杠杆的说法中正确的是 ( )
A.力臂一定在杠杆上 B.杠杆一定是硬棒,且一定要有支点
C.杠杆越长使用时越省力 D. 有的杠杆既省力又省距离。
*【变式训练1】:是非判断题: ①杠杆一定是直的( ) ②杠杆一定是硬棒( )
③杠杆一定要有支点( ) ④力臂是支点到力的作用点的距离( )
⑤有的杠杆既省力又省距离( ) ⑥力的作用线通过支点,这个力不会破坏杠杆的平衡( )
⑦力臂绝不可能等于支点到力的作用点的距离( )
⑨力臂是支点到力的作用线的距离( ) ⑩杠杆的长度等于动力臂与阻力臂之和( )
【点拨】:力臂是支点到动力作用线的距离,作法一般是从支点向力的作用线作垂线(画成虚线),作出的垂线即力臂,力臂不一定就在杠杆上。如果力的作用线刚好经过支点,则所对应的力臂就为0。
*【例3】:(1)用铅笔画出图10-3中这个杠杆受到的阻力F2的示意图,以及力F1的力臂。
(2)在上图10-4中画出以上三个杠杆模型的力F1、F2的力臂?
?1、2。
【提醒】:动力和阻力的作用点一定要画在在杠杆上,不要把作用点画在重心上而画成 “重力示意图”
【变式训练2】:下列关于F1力臂的作图中,正确的是( )
【点拨】:如何正确的画出力臂:一找支点、二画线、三连距离、四标签。即分为以下4步:
⑴支点O;⑵画力的作用线(虚线);⑶画力臂(虚线,过支点垂直力的作用线作垂线);⑷标力臂(大括号)
*【例4】:如下图10-6:先在图中做出此杠杆的五要素,然后用字母符号在对应的位置标出杠杆的五要素:支点用符号 表示;动力用符号 表示;动力臂用符号 表示;阻力用符号 表示; 阻力臂用符号 表示。杠杆平衡条件的数学表达式 :乘积式: . 比例式: .
;
【变式训练3】:铡刀在使用时的受力情况如图10-7所示,某学生在图中分别作出了F1和F2的力臂L1和L2,其中 的作法不对。(选填“L1”、“L2”、“L1和 L2”)
【解析】:读图可知,动力的力臂L不是从“支点”到动力作用线的距离,而是从 “物体的中心”到动力作用线的距离,因此不符合力臂的要求.图中重新标注部分才是动力的力臂.
【例5】:如果把铁锨看作是费力杠杆,在图10-8中所示的A、B、C三点中,支点是 点,动力作用点是 点,阻力作用点是 点。
【解析】:在铁锨的使用中,人的左手用力下压,而右手用力上抬,使铁锨抬起来。由此可见,人的左手充当支点,右手给杠杆提供动力,铁锨上的重物对铁锨的压力就是铁锨向上的阻力。所以,A点是阻力作用点,B点是动力作用点,C点是支点。
*【例6】:如图10-9所示,请画出杠杆在图示位置静止时作用在A点的最小动力F及其力臂。
【解析】:作图原理:力和它的力臂成反比,所以动力臂最长时对应的动力最小。又根据动力与动力臂垂直,因此:从动力的作用点做动力臂的垂线,即为最小动力。
以此题为例: 作最小动力的方法步骤:①第一步:找到离支点最远的点为动力作用点A;②第二步:连接支点O和动力作用点A,即为最长的动力臂;③第三步:在A点作动力臂的垂线——带剪头的垂线。即为最小的动力(力的方向不要画反)。
#【变式训练4】:一直径是100厘米、重量是400牛顿的均匀圆桶放在水平地面上,并靠在高10厘米的台阶边,如右图所示。小明要在圆柱体边缘最小施多大的力才能使圆桶滚上
台阶?画出这个力。 解:
【解析】:首先要构建杠杆模型,不要让物体束缚住了思路。如图,重力的
作用点在中心,方向竖直向下,即为阻力F2,阻力与阻力臂的乘积
不变,由F1×L1=F2×L2=常数,则动力臂最长(直径)时动力最小,此
时动力的作用点在支点和圆心的连线与圆的交点上,动力方向垂直于直径
斜向上。
*【变式训练5】:如图10-11所示的杠杆,要使杠杆平衡,在A端施加的最小作用力是________。 《2》
【解析】:由图可知,动力F2与OA垂直,则动力F (?http:?/??/?www.21cnjy.com?)2对应的动力臂就是OB,它是最长的动力臂.由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小.因为F?对应的动力臂最长,所以F?最小.
【例7】:有关杠杆作图的再巩固:
(1)下图左质地均匀的木棒AB重为100N,作出下图中对木棒AB拉力的力臂和木棒AB受到的重力的示意图.
(2)在图10-2的起钉锤中,请用铅笔:⑴画出锤子所受阻力F2的力的示意图;⑵画出动力F1的力臂.
(3)如下图右图是列车上售食品的手推车,当前轮遇到障碍物时,售货员向下按扶把,使手推车前轮向上翘起,请画出售货员所用的最小动力及其力臂.
【解析】:(1)过木棒的重心沿竖直向下画一条带箭头的线段,并用G表示;过支点B作拉力作用线的垂线段,即为拉力的力臂l1,答案见答案卷:(2)(3)作图也见答案卷。
*【例8】:如图10-1-16所示,O为杠杆的支点,OA=40cm,OB=50cm,B点
所挂物体重60N,要使杠杆在水平位置平衡,则在A点至少加一个竖直向上
牛的动力,这是一个 (选填“省力”或“费力”)杠杆。
【解析】:由图可知,O点为支点,OA为动力臂,OB为阻力臂,阻力大小等于所挂物体的重力,在A点的拉力为动力;由杠杆的平衡条件可知:动力F=60N×0.5m /0.4m =75N>60N;因为动力大于阻力,所以这是一个?杠杆.
【例9】:如图所示是正在进行的赛艇比赛,以下说法正确的是( )
A.赛艇的浆是省力的杠杆
B.赛艇的头部做得很尖是为了增大压力
C.赛艇能够前进是利用了物体间力的作用是相互的
D.赛艇能漂浮在水面上是由于它所受的浮力大于重力
【解析】:A、赛艇的桨在使用过程中,动力臂小于阻力臂,是费力杠杆,省距离,故A错误;
B、赛艇的头部做得很尖是为了减小水的阻力,故B错误;
C、当赛艇前进时,赛艇的桨给水一个向后的力,因为物体间力的作用是相互的,水就会对桨产生一个向前的力,使赛艇前进,故C正确; D、因为赛艇漂浮在水面上,所以F浮=G总,故D错误; 故选
*【例10】:如下图是安装在安全文明小区进出口的栏杆(栏杆是一根粗细均匀的木杆)示意图,当在 A处施加一个压力F时,可将栏杆拉到如图所示位置,请在图中画出此时压力F的力臂L1,和重力G的力臂L2。
【例11】:在上面右图中,要将书桌的C点轻轻抬起,请在图中画出最小的动力F1及其力臂。
专题二:杠杆的平衡条件及其应用
*【例1】:如下图:是何勇同学在探究杠杆的平衡条件:
(1)何勇同学把杠杆放在水平台面上,如图甲,为了使杠杆在水平位置上平衡,这时应将左边的螺母A向_______调(选填“左”或“右”),他这样做的目的是为了____________________________________。
(2)在实验的过程中出现如图乙所示的情况,为了使杠杆在水平位置上平衡,他应将左侧的钩码向_______移动。他在实验时使杠杆在水平方向平衡的目的是________________________________________________。
(3)物理探究中有一个很重要一步是提出一些猜想。在本实验中有同学猜想,杠杆平衡的条件可能是“动力+动力臂=阻力+阻力臂”,你认为他的猜想合理吗?说出原因。
(4)下表是小华得到的一组实验数据。
动力F 1 /N 动力臂l1/cm 阻力F2/N 阻力臂l2/cm
3 4 4 3
由此她得出“动力+动力臂=阻力+阻力臂”的结论。你认为她的实验结论是否正确?如果不正确,造成错误的原因是什么? 。
(5)如上图10-01是另一位同学——小明 “探究杠杆平衡条件”的实验装置。
①用铅笔画出图10-01中F2的力臂L2; ②用铅笔画出图10-01中F1’的力臂L2’. 《3》
(6)每个钩码均重0.5N,如图10-01所示,在杠杆右侧改为用弹簧测力计竖 (?http:?/??/?www.21cnjy.com?)直向下拉,此时弹簧测力计示数为F1,当弹簧测力计逐渐向右倾斜处于F1’的位置时,使杠杆仍然在水平位置平衡,则弹簧测力计的示数为
F1’则 F1 F1’(选填:大于、小于、等于),其原因是F1’的力臂要比F1的力臂 。
(7)本实验得出杠杆的平衡条件是:_____________________。
【解析】:在探究杠杆平衡条件时,两次使杠杆平衡,一次是实验前,调节平衡螺母,使杠杆在水平位置平衡,这样是为了消除杠杆自重对实验结果的影响和便于测量力臂;第二次是在实验过程中,调节钩码的个数和位置,使杠杆再次在水平位置平衡,这是为了便于测出杠杆的力臂。(7)F1L1=F2L2
【解答】:(1)右 消除杠杆自重对实验结果的影响(或:便于测量力臂) (2)左的钩码向左移(或把右边的钩码向左移;或减少右边的钩码数量等) 便于测出杠杆的力臂 (3)不合理。力和力臂是不同的物理量,不能相加。 (4)不正确,一次实验得出实验结论具有偶然性,得多做几次实验。(5)①②作图略; (6) 根据“力和它的力臂成反比”,当弹簧测力计逐渐向右倾斜时,F1’的力臂变小,对应的拉力就增大。
【点拨】:在探究杠杆平衡条件的实验中要“两次”使杠杆在水平方向平衡,第一次是实验前,调节平衡螺母;第二次是调节钩码的位置,使杠杆在水平方向平衡。
【变式训练1】:在做研究杠杆平衡的条件实验时,小红根据如图10-1-7甲所示的实验现象得出的杠杆平衡条件是:“动力×支点到动力作用点的距离=阻力×支点到阻力作用点的距离”。为了说明这一结论并不正确,请你在图乙所示的杠杠上画出需要对杠杠施加的力的示意图和这个力的力臂。
【解析】:在A点或者B点沿不同方向拉弹簧测力计,使杠杆在水平位置平衡。现象是:力的方向改变,力的大小也发生改变。动力×支点到动力作用点的距离≠阻力×支点到阻力作用点的距离,但是却始终满足动力×动力臂=阻力×阻力臂。作图参看答案。
【例2】:如图10-1-8所示,质量可忽略的杠杆上所标的每一格长度都是相等的,O为支点,杠杆两边所挂的每一个钩码均相同,杠杆在水平位置平衡。在下列情况下,杠杆仍在水平位置保持平衡的是( )
A.两边都减少一个钩码 B.两边的钩码下各加挂一个相同的钩码
C.左边钩码向右移一格,右边钩码同时向左移一格
D.右边钩码下加挂一个相同的钩码,左边钩码同时向左移一格
【解析】:图中左边:力×力臂=2×3 = 6,右边:力×力臂=3×2 = 6,杠杆在水平位置平衡。A中两边都减少一个钩码,左边:力×力臂=1×3 = 3,右边:力×力臂=2×2 = 4,杠杆不平衡,右端下降。A选项错。同理,我们可分析出B、C选项错。D选项中,左边:钩码同时向左移一格后,力×力臂= 4×2 = 8,右边:加挂一个相同的钩码后,力×力臂= 4×2 = 8,杠杆可以继续在水平位置保持平衡。所以选?
*【变式训练2】:如图6-5-3所示,挂着的各个钩码质量相等,杠杆处于平衡状态,当两边钩码下各增加1个同样的钩码时( ) A.杠杆左端下降 B.杠杆右端下降
C.杠杆仍然平衡 D.无法判断
【解析】:杠杆平衡的条件是:“左右两侧力和力臂的成绩相等”。
【解答】:增加钩码前,杠杆平衡,则有2G·3L=3G·2L(设每个钩码重为G,每段杆长都为L),左右两边都增加一个钩码,左边力和力臂的乘积变为3G·3L,右边力和力臂的乘积变为4G·2L。因为左边力和力臂的乘积>右边力和力臂的乘积变,所以杠杆左端下降。
#【变式训练3】:不等臂直杠杆在动力和阻力作用下,已经处于平衡状态,采用下列办法不能使杠杆平衡的是 ( ) A.在杠杆上再施加一个力,使这个力的作用线通过杠杆的中点,但不通过支点
B.在杠杆上再施加一个力,使这个力的作用线通过支点
C.使动力和阻力同时减小到原来的1/2 D.使动力臂和阻力臂同时变为原来的2倍
【解析】:杠杆平衡条件是动力×动力臂 = 阻力×阻力臂,不论改变力还是改变力臂,只要满足杠杆的平衡条件,则杠杆仍然平衡。沿力的方向画的一条直线称为力的作用线,在杠杆上施力,但这个力的作用线通过杠杆的支点,则这个力的力臂为零,不影响杠杆的平衡。在杠杆上再施加一个力,使这个力的作用线通过杠杆的中点,但不通过支点,所加的这个力不能满足动力×动力臂 = 阻力×阻力臂,则这个力不能使杠杆平衡
【例3】:如图10-1-10所示,用一根木 (?http:?/??/?www.21cnjy.com?)棒撬大石头,没有撬动,为了撬动大石头,应将垫在木棒下的小石块向 移动,这实质上是增大了 ,同时又减小了 。
【解析】:小石块向左移,增大了动力臂,同 (?http:?/??/?www.21cnjy.com?)时又减小了阻力臂.在动力和阻力
不变的情况下,动力和动力臂的乘积才会大于阻力和阻力臂的乘积,才会撬动
大石头.故答案为:
【变式训练4】:如图10-1-11,杆秤是民间的一种测量工具。使用时,将待
测物体挂在秤钩A上,用手拎住秤钮B或C(相当于支点),秤砣D在秤杆E上
移动,当杆秤水平平衡时就可以在秤杆上读出读数。
(1)从科学的角度来看,杆秤应该是一种测量 大小的工具。
(2)根据杠杆平衡的条件分析,使用杆秤时,当从秤纽C换到秤纽B时,
杆秤的测量值将变 。
【解析】:杆秤是用来测量物体质量的一种测量工具,是杠杆的应用。根据杠杆
平衡条件F1L1 = F2L2可知,被测物体离称钮越近,即力臂越短,被测物体的质量就越大。所以当从秤纽C换到秤纽B时,杆秤的测量值将变大。
*【例4】:如图6-5-4所示,下列器件中属于费力杠杆的是( ) 《4》
(?http:?/??/?www.21cnjy.com?/??)
【解析】:根据杠杆平衡条件,省力杠杆是动力臂大于阻力臂的杠杆。瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆.核桃夹子在使用过程中,动力臂大于阻力臂,是省力杠杆.钳子在使用过程中,动力臂大于阻力臂,是省力杠杆.镊子在使用过程中,动力臂小于阻力臂,是费力杠杆.故答案为?
【变式训练5】:如下图所示的工具中,正常使用时属于省力杠杆的是( )
【解析】:根据杠杆平衡条件,动力臂大于阻力臂的杠杆为省力杠杆;动力臂小于阻力臂的杠杆为费力杠杆;坩埚钳由于动力臂小于阻力臂是费力杠杆;筷子夹菜时由于动力臂小于阻力臂是费力杠杆;镊子夹取物体时,动力臂小于阻力臂是费力杠杆;B图为剪铁皮的剪刀,其动力臂大于阻力臂,是省力杠杆。 故答案为。
【例5】:如图是吊车起吊贷物的结构示意图,伸缩撑杆为圆弧状,工作时它对吊臂的支持力始终与吊臂垂直,使吊臂绕O点缓慢转动,从而将货物提起
.下列说法正确的是( )
A. 吊臂是一省力杠杆,但要费距离
B. 吊臂是一个费力杠杆,但可以省功
C. 匀速顶起吊臂的过程中,伸缩撑杆支持力的力臂变小
D. 匀速顶起吊臂的过程中,伸缩撑杆支持力渐渐变小
【解析】:由图可知,伸缩撑杆的阻力臂大于动力臂,所以吊臂是一个费力杠杆,A错误;机械可以省距离,但不能省功,B错误;伸缩撑杆为圆弧状,伸缩时对吊臂的支持力始终与吊臂垂直.则动力臂保持不变,在伸缩撑杆匀速顶起吊臂的过程中,重物的阻力臂逐渐减小.由杠杆的平衡条件可知伸缩撑杆受到支持力渐渐变小。
【例6】:如下图所示是安置在巴中大佛寺收费站栏杆的示意图,当在A处施加一个动力时,可将栏杆拉起来,它是一根( ) A.省力杠杆 B.费力杠杆 C.等臂杠杆 D.无法确定
【解析】:从支点到动力作用线的距离叫做动力臂;从支点到阻力作用线的距离叫做阻力臂.动力臂大于阻力臂的杠杆为省力杠杆;动力臂小于阻力臂的杠杆为费力杠杆;由图可知杠杆绕A点右侧的轴转动,A点右侧的轴为支点,则作用在A点的动力的力臂远远大于杠杆重力的阻力臂,所以此栏杆是一个费力杠杆.选?.
【知识点补充】:
生活中的“省力杠杆”:撬棍、羊角锤、瓶盖起子、老虎钳、起子(开瓶器)、手推车、剪铁皮和修剪树枝的剪刀、杆秤、动滑轮、道钉撬、裁衣剪刀、指甲刀、核桃夹、自行车刹车闸等。
生活中的“费力杠杆”:筷子、镊子、钓鱼竿、脚踏板、扫帚、船桨、理发剪刀、起重机(起重臂),人手臂(胳膊),食品夹子、缝纫机的踏板等
【等臂杠杆】:天平、定滑轮,(跷跷板?)
*【变式训练6】:图6-5-23所示是一个指甲刀的示意图,它由三个杠杆ABC、OBD和OED组成,用指甲刀剪指甲时,下面说法正确的是( )
A.三个杠杆都是省力杠杆 B.三个杠杆都是费力杠杆
C.ABC是省力杠杆,OBD、OED是费力杠杆
D.ABC是费力杠杆,OBD、OED是省力杠杆
【解析】:指甲剪可以看成是由一个撬棒和一个镊子组成:
①撬棒是ABC,以B为支点,动力作用在A上,阻力作用在C上,使用时动力臂大于阻力臂,是省力杠杆;
②镊子是由OBD和OED两个杠杆组成,支点O点,动力作用在E点,阻力作用在D点.使用时动力臂小于阻力臂,是费力杠杆.故答案为
【友情点拨】:对于类似的实际中使用的杠杆,要善于从实际的工具中抽象出具体的杠杆模型。在确定杠杆的几个要素时,要抓住研究对象是杠杆,在确定杠杆的支点时,可以设想让被研究的工具动一动,在动的过程中,便可确定固定不动的点,即支点;再结合杠杆平衡条件来分析杠杆的省力或费力情况。
*【例7】:如图所示,杠杆AOB用细线悬挂起来,分别在A、B两端分别挂上质量为m1、m2的重物时,杠杆平衡,此时AO恰好处于水平位置,AO=BO,不计杠杆重力,则m1、m2的关系为( )
A.m1>m2 B.m1<m2 C.m1=m2 D.无法判断
例7题图 图10-1-8 例8题图
【解析】:根据杠杆的平衡条件:F1L1=F2L2可知,G1L1=G2L2,m1gL1=m2gL2,即m1L1=m2L2,力与相应的力臂成反比关系,从图中可以看出力臂L1>L2,所以物体的重力G1<G2,那么质量m1 m2的大小关系可知。
【变式训练7】:如上图10-1-8所示,A点的弹簧测力计无论是竖直向下还是倾斜向下都可以使杠杆平衡,由杠杆的平衡条件可知( )
A.倾斜拉动,弹簧测力计的示数较大 B.竖直拉动,弹簧测力计的示数较大
C.两种方法弹簧测力计的示数相等 D.无论弹簧测力计怎样拉动,弹簧测力计的示数都小于物重
【解析】:力臂是支点到力的作用线的距离,竖直向下拉弹簧的力臂(5格长)最大且大于左端拉力力臂(3格长),此时拉力小于物重且最小;倾斜拉,完全有可能出现弹簧拉力力臂大于、等于、小于左边的拉力力臂,所以弹簧拉力会有小于、等于、大于物重的可能性. 《5》
*【例8】:如图所示,杠杆的支点O,在A端加一个动力(图中未画出),使杠杆在水平位置平衡,则杠杆( ).
A.一定省力 B.一定费力 C.不省力也不费力 D.以上三种情况均有可能
【解析】:如图所示的杠杆,在水平位置平衡,阻力作用在B处,所以阻力臂是一定的,即OB;动力作用在A端,当动力方向竖直向上时,动力臂最长是OA,OA大于OB,是省力杠杆,能省力;若动力方向不是竖直向上时,动力臂一定小于OA,但有可能大于OB,此时,也是省力杠杆,能省力。动力臂也有可能等于阻力臂OB,即动力臂等于阻力臂,是等臂杠杆,既不省距离也不省力;动力臂也有可能小于阻力臂OB,即动力臂小于阻力臂,是费力杠杆,费力但省距离。故此杠杆也可能省力,也可能费力,也可能不省力也不费力。故选?
【变式训练8】:请你仔细观察如右图所示的漫画,究竟小猴和小兔谁分的萝卜重?简要说明理由。
答:
【解析】:参看《同步学习》68页第8题。此题中小猴和小羊在分萝卜时利用了杠杆的平衡,用支点使萝卜处于水平位置的平衡。表面看来兔子要的那头多或者有人认为两边一样多,但是实际上就像小猴所说兔子中计了,小猴拿的那个比较重。根据杠杆的平衡条件,在杠杆平衡的条件下,力臂越大则力越小,而小猴那块的重心离支点近,力臂小;小兔那块重心离支点远,力臂大。所以小猴那块要比小兔那块重。
*【例9】:如图10-13所示,作用在杠杆一端且始终与杠杆垂直的力F,将杠杆缓慢地由位置A拉至位置B。在这个过程中,动力F_________(选填“变大”、“变小”或“不变”)
图10-13 图10-14
【解析】:根据杠杆平衡的条件,当杠杆的力臂发生变化时,相对应的力也会跟着变化。在研究杠杆变化的问题时,还要用到控制变量的方法。在本题中不变的物理量为阻力G和动力臂l1,阻力臂在变化,所以动力也随之变化。 【解答】:由题意可知,阻力G和动力臂l1没有发生变化(如上图所示),在提升时阻力臂l2变大,根据杠杆平衡条件Fl1=Gl2,动力F在变大。
*#【变式训练9】:如上图10-14所示杠杆,力F方向始终竖直向上,当此杠杆在动力F作用下,将一个由细绳系的物体由图中位置逆时针匀速转动到水平位置时,则 ( )
A.F大小始终不变? B.F变大? C.F先变小后变大 D.无法判断F大小的变化
【解析】:根据相似三角形,动力臂和阻力臂的比值不变,等于支点到力的作用点的长度之比,阻力不变,所以动力F始终不变。如图乙所示画出杠杆的力臂,在提升重物时,阻力臂l2在变小,动力臂l1也在变小。但可以把杠杆平衡的条件写成杠杆的比例式:F1/F2=L2/L1,其中F2=G物,利用数学上的相似三角形可知,在提升时,L2/L1的大小是不变的,F2(G物)没有变化,所以提力F1的大小?
【变式训练10】:如下图甲所示,刘刚同学在利用一根扁担抬起一个水桶,她用一个始终向上的力把这个水桶提离地面。他把水桶抬离地面一个较小的高度的过程中,提力F________。(填“变大”“变小”“不变”)
【变式训练9】图甲 【变式训练9】图乙 【例10】题图
【解析】:思路点拨:分析杠杆在变化时,要首先明确杠杆要素中哪些要素在变。如图乙所示画出杠杆的力臂,在提升水桶时,阻力臂l2在变小,动力臂l1也在变小,所以无法直接判断F的大小如何变化。但可以把杠杆平衡的条件变化为比例式,我们能否比较的大小如何变化呢?利用数学上的相似三角形可以知道,当在提升时,L2/L1的大小是不变的,阻力G没有变化,所以提力F的大小?
【例10】:某同学做探究杠杆平衡条件的实验.(1)实验时,为了方便对力臂的测量 (?http:?/??/?www.21cnjy.com?),该同学先调节平衡螺母,使杠杆在 位置平衡;这是为了便于 。并通过多次实验才能总结出杠杆的平衡条件,多次试验的目的是为了排除实验的 ,寻找普遍规律.
(2)实验中,在杠杆上的A点挂四个重均为 (?http:?/??/?www.21cnjy.com?)0.5N的钩码,用调好的弹簧测力计竖直向上拉杠杆上的B点,使杠杆水平平衡,如上图右图所示,测力计的示数是 N;如果将测力计沿图中虚线方向拉,仍使杠杆在水平位置平衡,则测力计的示数将 (变大/不变/变小).
【解析】:(1)答案为:水平;测量力臂;偶然性。(2)弹簧测力计竖直向上拉杠杆时,动力臂是OB,当弹簧测力计倾斜拉杠杆时,阻力和阻力臂不变,但因为动力和动力臂成反比。当动力臂减小时,动力就会变大.
【例11】:将重为80牛的物体挂在1.8米长的杠杆一端,在另一端加上16牛的动力
时杠杆平衡,则动力臂与阻力臂之比为 (提示:用杠杆平衡条件的“比例式”
求解更简单);动力臂长为 米。
【解析】:杠杆平衡条件的比例式:L1 /L2=F2 /F1可以求出动力臂与阻力臂之比L1 /L2=F2 /F1=80 /16=?再将L2=1.8- L1, F1=16N, F2=G=80N,代入杠杆平衡条件公式F1L1=F2L2,可以求出动力臂L1。
【变式训练11】:如右图2是一种拉杆式旅行箱的示意图,使用时相当于一个 力
(填“省”或“费”)力杠杆;若箱和物品共重100N,动力臂是阻力臂的5倍,则抬起拉杆的力至少为 N。
【例12】:小明在学校参加植树活动时,使用如图10-1-4所示的钢丝钳,剪铁丝固定小树苗。
(1)他使用的钳子是省力杠杆还是费力杠杆?(2)在图中画出动力F1的力臂L1
和作用在这根杠杆上的阻力F2。 (3)剪铁丝时动力臂长为10cm,阻力臂长为2cm,若铁丝被剪断需要1000N的力,小明至少用多大的力才能将铁丝剪断?
解:
6》
专题三:综合提升练
【例1】:如下图10-16杠杆在力F1 ,F2作用下处于平衡状态,L1为F1的力臂。请在图中作出F2的力臂L2及力Fl。
【解析】:过L1的端点做垂直于L1的垂线,与杠杆的交点即为动力作用点,为使杠杆平衡,方向向上;
从支点到F2作用线的距离即为L2,过L2的端点做垂直于L1的垂线,就是力Fl。 答案见答案卷
图10-16 图10-17 图10-18
【变式训练11】:如图10-17,杠杆OA在力F1、F2的作用下静止,l2是F2的力臂,画出F1的力臂和力F2
【解析】:类同【例1】的解析。
【例2】:如图10-18所示,在“研究杠杆平衡条件”的实验中共有5个相同的钩码供选择,杠杆上每格距离相等,先将杠杆在水平位置调节平衡后,在杠杆左边离支点O三格的A处挂了2个钩码。为使杠杆的水平位置平衡,如果只在支点右边挂钩码,请你回答所挂钩码的位置和钩码的个数: (只回答一种方法即可)。
【例3】:一根重100牛顿的均匀直铁棒放在水平地面上,抬起一端所需最小的力是( )
A.50牛顿. B.75牛顿. C.25牛顿. D.100牛顿.
【解答】:需要50N 。因为它的重心在中点处 我们的力施加在一端。这样 动力臂和阻力臂之比是2:1, 所以动力与阻力之比是1:2,因为力和它的力臂成反比:F1/F2=L2/L1;抬起一端所需最小的力是。
【例4】:如图6-5-13所示,用撬棒撬一块大石头,已知棒AB=0.7m、BC=0.2m、CD=0.1m,撬棒在C 处受到石头的压力为2000N,欲撬动石头,所用的力必须大于多少?(棒的自重不计)要求:用两种方法并通过具体计算,判断得出结果。
【解析】:撬棒在使用过程中,作用在A点上的动力F即可向上也可向下、或其它方向,但因题目要求用两种方法求解,且每种方法均要求所用的力要最小,所以作用在A点的力必须与杆AB垂直。
解答:(1)若作用在A点的力沿斜下方且与杆AB垂直,则杆将绕着B(支)点转动,根据杠杆的平衡条件F1L1=F2L2可知,此时杠杆的动力臂L1=AB=0.7m,阻力臂L2=BC=0.2m,欲撬动石头,作用在杠杆A点上的最小力应为
(2)若作用在A点的力沿斜上方且与杆AB垂直,则杆将绕着D(支)点转动,根据杠杆的平衡条件F1L1=F2L2可知,此时杠杆的动力臂L1=AD=0.7m+0.2m+0.1m=1m,阻力臂L2=BC=0.1m,欲撬动石头,作用在杠杆A点上的最小力应为:
【例5】:小柯积极参加体育锻炼.如图所示为 (?http:?/??/?www.21cnjy.com?)他在练习俯卧撑.此时他的身体可看为一个杠杆,O点是支点.他的重力为600N,所受重力可视为集中在A点.将身体撑起时,(1)地面对双手的支持力至少多大?(2)若每个手掌的面积为0.02m2,双手对地面的压强有多大?
【解析】:(1)将人体视为杠杆,支持力F的力臂为L1=1.2m;重力G的力臂L2为0.8m;
由杠杆的平衡条件得:FL1=GL2,即F×1.2m=600N×0.8m;则F=400N,地面对双手的支持力至少为?N.
(2)解答:力的作用是相互的∴双手对地面的压力等于支持力:F压=F1=300N;再根据压强公式(定义式)
两个手掌的总面积为0.02m2×2=0.04,m2 。将压力和受力面积代入压强公式 P=F/S即可求出压强。
解:
【例6】:如图所示,秤砣的质量 (?http:?/??/?www.21cnjy.com?)为100g,秤杆的质量忽略不计.秤杆水平静止时,OA=5cm,OB=25cm,则被测物的质量为 kg.若秤砣有缺损时,则杆秤所示的质量值 (填“偏大”或“偏小”).
【变式训练12】:已知物体在月球上的重力大约是地球上重力的六分之一。做生意时,用同一杆秤在月球上称质量,和在地球上相比( )
A. 买方吃亏 B. 卖方吃亏 C. 双方都不吃亏 D. 双方都吃亏
【解析】:到月球上后,动力臂和阻力臂都不变,而动力和阻力都变为原来的1/6,所以杠杆依旧平衡,所以
【例7】:两个质量相等的实心的铜球和铁球(ρ铜>ρ铁),分别挂在杠杆的两端,杠杆平衡。现将两球同时浸没在水中,杠杆( ) A.不平衡,挂铜球一端下降 B.不平衡,挂铁球一端下降
C.仍然平衡 D.无法判断
【解析】:受力分析一下:铜球和铁球两个质量相等,G铜=G铁。同时浸没在水中,因为ρ铜>ρ铁,m铜=m铁,所以V铜小于V铁G ,F浮铁> F浮铜,铁块受到的竖直向上的浮力大,所以挂铜球一端下降。 A
#【例8】:如下图10-1-7所示,一根粗细均匀的硬棒AB被悬挂起来,已知AB=6AO,当在A处悬挂一重为100牛的重物时,杠杆恰好平衡,杠杆自身的重力多大。
#【例9】:如图10-1-9所示,一支均匀的直尺放在水平桌面上,一端
伸出桌面,已知伸出桌面的部分是全尺的三分之一。当在B端挂一个5N重物时,
直尺的A端刚刚开始翘起,则此木尺的重力是______N。
#【例10】:如图10-1-10所示,直径为36cm的半球形碗固定在水平面上,碗的端口水平。一根密度分布均匀、长度为47cm的光滑杆ABC搁置在半球碗上,碗的厚度不计,杆平衡时碗内部分AB段与碗外部分BC段的长度之比为(? ?) 《7》
A.38:9 B.35:12 C.32:15 D.27:20
#【例11】:如图8所示,AO=40厘米,BO=20厘米,拉力F=3牛,并与水平
方向成30°角。若在木棒B端悬挂体积为100厘米3的物体G,并将它浸没在
水中,木棒恰好平衡,则物体的重力应为多大?
【同步跟踪练习】
1.如图10-1-11所示,杠杆调平衡后,在A处挂3个钩 (?http:?/??/?www.21cnjy.com?)码,要想杠杆继续平衡,则需在B处挂 个钩码.杠杆在水平位置平衡后,两侧各去掉一个钩码,则杠杆的 端将上升.(每个钩码的质量都相同)
解答:(1)由题意可知,杠杆在水平位置平衡,设一个钩码的重力为G,一个格为L,由杠杆平衡条件可知,3G×5L=nG×3L,解得:n=5;所以在杠杆右边B处应挂5个够码. (2)如果A、B两处各去掉一个钩码,左边:2G×5L=10GL,右边:4G×3L=12GL,所以左端小于右端,右端下降,左端将上升. 故答案为
2.用杠杆撬起一块重1000N的石块,如果动力臂长100cm,阻力臂长10cm,那么用_____N的力就可以了.
3、如图10-1-12所示,B端悬挂一重为G的重物,不计杠杆自重,在A点施加动力F使杠杆保持水平平衡.则下列说法正确的是( ?)
A.当杠杆平衡时,一定满足G×OB=F×OA
B.因为OA大于OB,所以F小于G
C.杠杆可能为等臂杠杆 D.动力的方向一定竖直向下
4、如图所示,杠杆的左端悬挂着一个重物,右端用弹簧测力计拉着,使
杠杆在水平方向保持平衡。若将弹簧测力计缓慢地沿着图中虚线自位置1
移到位置2,并保持杠杆始终在水平方向平衡,则弹簧测力计的示数变化是( )
A.不断增大 B.不断减小 C.先增大,然后减小 D.先减小,然后增大
【思路点拨】:判断拉力的变化,就要分析拉力的力臂如何变化。在本题中弹簧测力计由1位置拉到2位置过程中,力臂是先变大后变小的,当拉力方向与杠杆垂直时力臂最大。
《§10.1、科学探究:杠杠的平衡条件》同步提升策略 《参考答案》
专题一:杠杆的五要素及其作图。
【典型例题】:【例1】:答案略。 【例2】:B。 【变式训练1】:②③⑥⑨是正确的,其它错。
【例3】:答案略。 【变式训练2】:C。 【例4】答案见10—1—1。 【变式训练3】:L1。
【例5】:C;B;A。 【例6】:见下图10—1—2。 【变式训练4】:见图10—1—2。L2=30厘米(50厘米的平方和40厘米的平方的开方)由F1×L1=F2×L2 得F1=F2×L2/L1=400N×30cm/100cm=120N。所以,小明要将圆柱体滚上台阶所需的最小作用力为120N。 【变式训练5】:F2。 【例7】:见图10-1-4的三幅图。 【例8】:75,费力。 【例9】:C。 【例10】:图10-1-5。 【例11】:见图10-1-6。
专题二:杠平衡条件及其应用
【例1】:【解答】:(1)右 消除杠杆自重对实验结果的影响 (2)左的钩码向左移(或把右边的钩码向左移;或减少右边的钩码数量等) 便于测出杠杆的力臂 (3)不合理。力和力臂是不同的物理量,单位不同,不能相加。(4)不正确,一次实验得出实验结论具有偶然性,得多做几次实验。(5)①②作图略;
③“<”;(6) “小于”,“短”。 (7)F1L1=F2L2
【变式训练1】:见图10-1-7。 【例2】:D。【变式训练2】:A。 【变式训练3】:A。【例3】:左,动力臂,阻力臂. 【变式训练4】:(1)质量 (2)大。 【例4】:D。 【变式训练5】:B。 【例5】:D。 【例6】:A。 【变式训练6】:C. 【例7】:B。 【变式训练7】:A。 【例8】:D。 【变式训练8】:小猴分得的萝卜重,如图所示,萝卜平衡时,粗的那端力臂短,根据杠杆平衡条件,粗的那端萝卜更重。
【例9】:变大。 【变式训练9】:A。 【变式训练10】:不变。 【例10】:(1)答案为:水平;测量力臂;偶然性。(2)变大。 【例11】:5:1;1.5. 【变式训练11】:省;20N。
【例12】:(1)省力杠杆;(2)图略。(3)解:根据杠杆平衡条件 ,可得
专题三:综合提升练
【例1】:图10-1-10。 【变式训练11】:见下图10-1-11。 【例2】:在两格出挂3个钩码。
【例3】:50牛
【例4】:(1) (2)
[答案] 两次所用的力分别为571N和200N。
【例5】:力的作用是相互的∴双手对地面的压力等于支持力:F压=F1=300N;
【例6】: 解:如图10-1-12所示: 因为杠杆平衡,所以G1LOA=G2LOB,
即:m1gLOA=m2gLOB,则m1===500g=0.5kg.
若秤砣有缺损,m2减小,而G1LOA不变,所以LOB要变大,杆秤所示的质量值要偏大.故答案为:0.5;偏大.
【变式训练12】:C。【例7】:A。【例8】:50N 【例9】:50N。 【例10】:C。 【例11】:B。
图10-1
图10-2
F1
图10-3 图10-4
图10-1 图10-1
图10-2 图10-3
L1
F1
F1
O
A
F1
L1
D
L1
C
F1
O
L1
B
图10-6 图10-7 图10-8
总结提升:力臂的画法:一找点,二划线,三作垂线段,四把力臂现(标力臂)。
A
图10-9
训练4图101010-10
B
O
A
F3
F1
图10—11
F2
总结提升:画最小动力的方法:①第一步:用虚线连接支点O和杠杆的最远端(动力作用点),即为最长的动力臂;②第二步:在动力作用点作动力臂的垂线。③判断所画动力的方向是否正确。
④根据动力和阻力使杠杆转动的方向相反,
图10-2
图10-1-16
例9题图
A
B
C
D
图10-01
甲
乙 22222
图10-1-7
总结提升:为什么要调节杠杆在水平位置平衡?如何调节?实验时为什么要做多次实验、收集多组数据?
实验前,先调节______________,使杠杆在水平位置平衡,这样做的好处是________________________
图10-1-8
图6-5-3
总结提升:判断一个杠杆在两个力的作用下是否处于平衡状态,是比较“两个力和各自力臂的乘积是否相等”,而不是单纯比较“力的大小” 或“力臂大小”。
图10-1-10
图10-1-11
D.镊子
图6-5-23
图 10-1-4
图6-5-13
图10-1-7
O
图10—1—9
图10-1-10
图10-1-11
图10-1-12
图10-1-12
10—1—3
F1
F2
图10-1-5
图10-1-1
F1
F2
A
图10-1-2
图10-1-4
图10-1-11
图10-1-12
10-1-6
F
10-1-7
10-1-10
1
11
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
