教科版高二物理选修3-4第一章 第2节单摆第1课时课件(共20张PPT)
文档属性
| 名称 | 教科版高二物理选修3-4第一章 第2节单摆第1课时课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-30 00:00:00 | ||
图片预览


文档简介
(共20张PPT)
秋千
风铃
吊灯
摆钟
摆钟
惠更斯摆钟
伽利略
惠更斯
§1.2 单摆
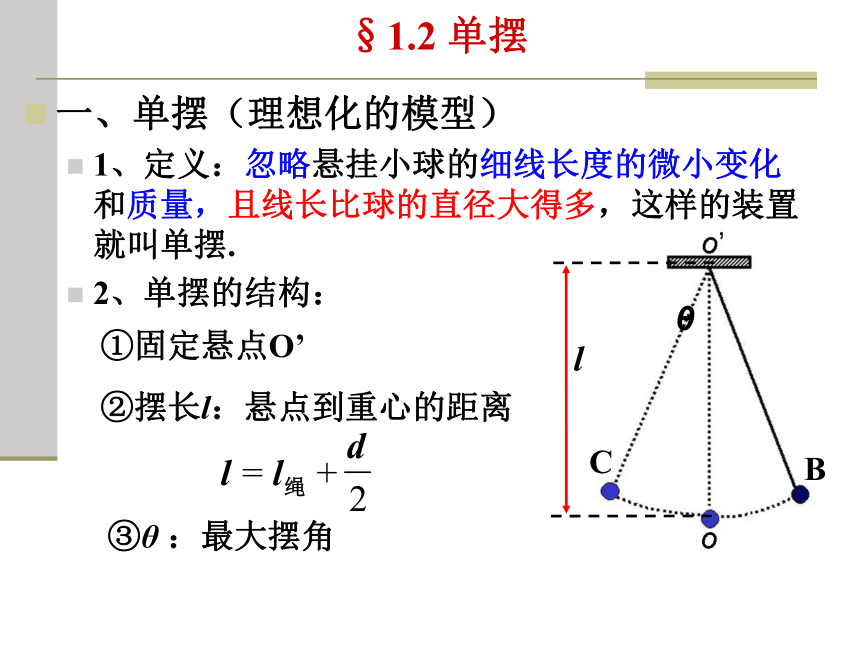
一、单摆(理想化的模型)
1、定义:忽略悬挂小球的细线长度的微小变化和质量,且线长比球的直径大得多,这样的装置就叫单摆.
2、单摆的结构:
①固定悬点O’
θ
②摆长l:悬点到重心的距离
l
③θ :最大摆角
B
C
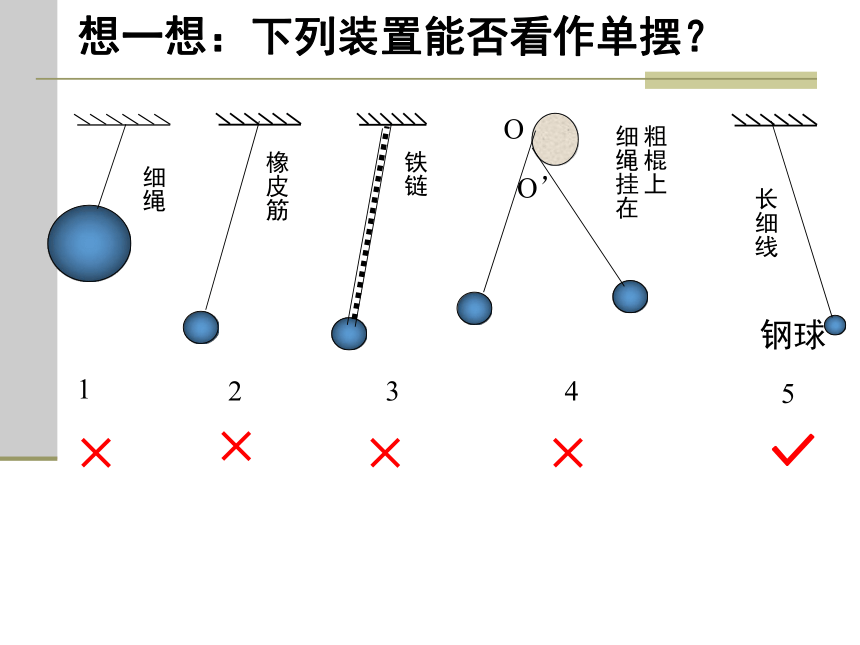
想一想:下列装置能否看作单摆?
?
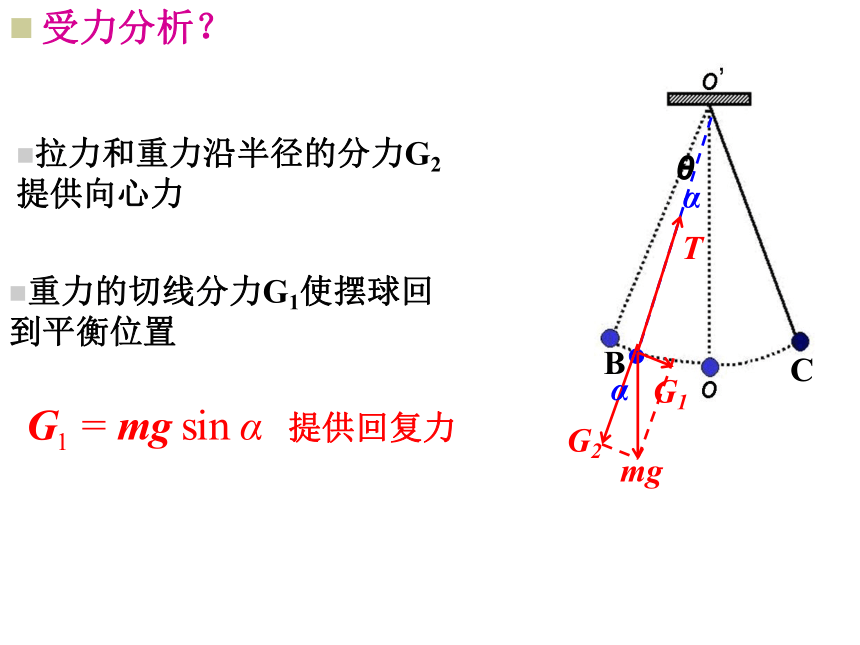
受力分析?
θ
C
拉力和重力沿半径的分力G2 提供向心力
重力的切线分力G1使摆球回 到平衡位置
提供回复力
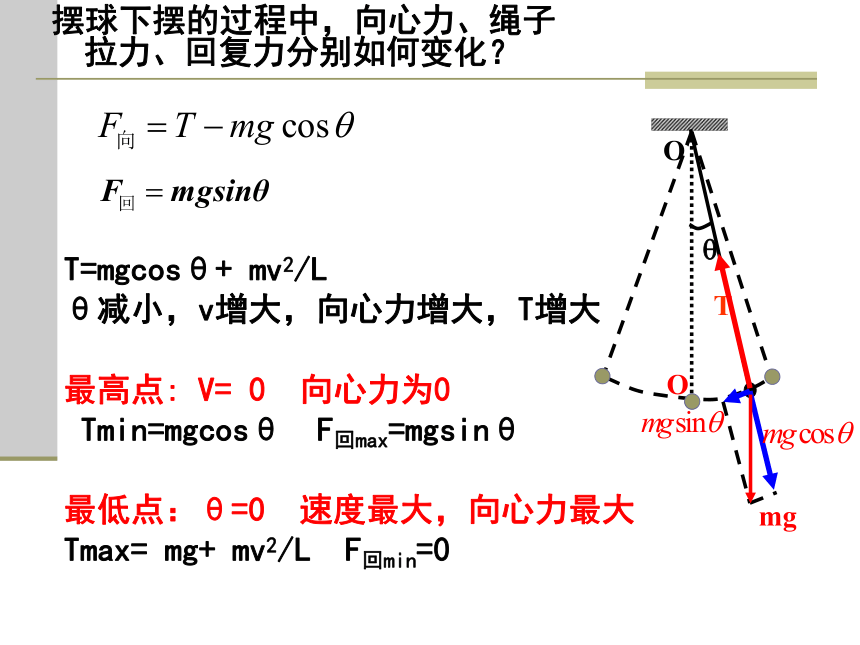
摆球下摆的过程中,向心力、绳子拉力、回复力分别如何变化?
T=mgcosθ+ mv2/L
θ减小,v增大,向心力增大,T增大
最高点: V= 0 向心力为0
Tmin=mgcosθ F回max=mgsinθ
最低点:θ=0 速度最大,向心力最大
Tmax= mg+ mv2/L F回min=0
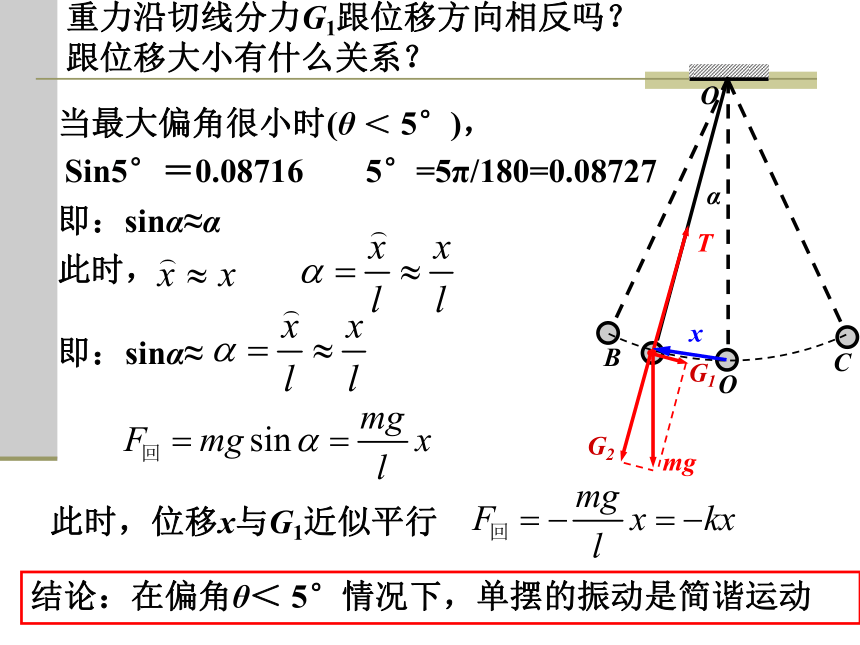
当最大偏角很小时(θ < 5°),
即:sinα≈α
Sin5°=0.08716
5°=5π/180=0.08727
此时,
即:
sinα≈
此时,位移x与G1近似平行
重力沿切线分力G1跟位移方向相反吗?
跟位移大小有什么关系?
结论:在偏角θ< 5°情况下,单摆的振动是简谐运动
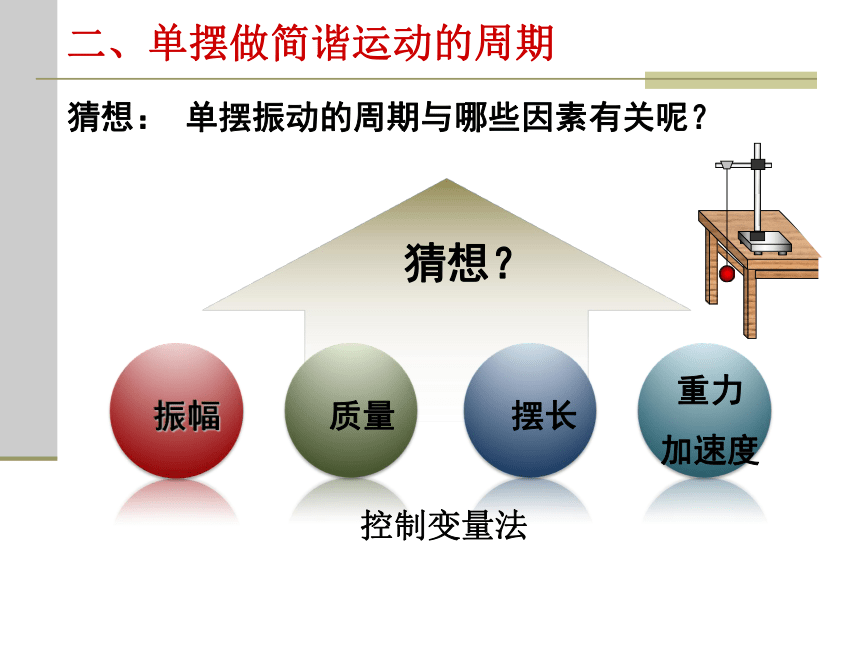
二、单摆做简谐运动的周期
重力
加速度
猜想: 单摆振动的周期与哪些因素有关呢?
控制变量法
伽利略18岁时,到教堂做礼拜,他发现吊灯摆动的幅度虽然慢慢地在变小,但摆动一次所用时间却没有变化。他用自己的脉搏的跳动次数来测算。终于肯定了吊灯摆动周期与摆动的幅度无关这个单摆摆动的等时性规律。后来他利用这个原理制成了一个 “脉搏计”,帮助判断病人患病的情况。
实验证明:(在重力加速度g不变时)
单摆振动周期与小球质量,振幅无关,与摆长有关;摆长越长,周期越长。
周期公式:
单摆做简谐运动的振动周期跟摆长的平方根成正比,跟重力加速度的平方根成反比。
1、计时器:惠更斯于1656年发明了世界上第一个用摆的等时性来计时的时钟。(1657年获得专利权)
三、单摆周期公式的应用
注意:无论快钟,慢钟,标准钟每摆动一次,指示的时间是相同的。
哈尔滨人在香港买的摆钟,到家后发现走时不准的原因是什么?是变慢了还是变快了?应该如何调整?
学以致用:
摆钟:利用单摆的等时性计时,摆的周期可通过改变摆长来调节.周期为2s摆长为1m的单摆叫秒摆.
2、 用单摆测定重力加速度
开动脑筋:
如果你在一座高山的山顶,你能用单摆测山的海拔高度吗?如果可以,还需要什么仪器?
(已知地球质量及地球平均半径)
实验:探究周期T与摆长L的关系
操作:
1、测摆长
2、测周期
实验:探究周期T与摆长L的关系
累积法测单摆周期:振动稳定后,小球某次经过平衡位置时开始计时并数“0”,再经过平衡位置数“1”,数到“n”停止计时,测出总时间t,求出周期的平均值T,T=t/2n
机械秒表使用:按动中间按钮启动计时,再按动按钮停止计时,按左侧按钮清零。
机械秒表读数:
长针:一圈30s,最小刻度0.1s,不估读
短针:一圈15min,最小刻度0.5min,不估读
电子秒表使用:按动中间按钮使显示屏显示如图,进入计时功能。按动右侧按钮开始计时,再按动右侧按钮停止计时,从显示屏直接读数。按动左侧按钮清零。
实验:探究周期T与摆长L的关系
实验:探究周期T与摆长L的关系
3.数据记录与处理
摆长(m) 30次振动时间(s) 周期(s)
① 0.2
② 0.4
③ 0.6
④ 0.8
⑤ 1.0
3、数据记录与处理
摆长(cm) 周期(s)
①
②
③
④
⑤
⑥
⑦
⑧
⑨
20.00 0.90
30.00 1.10
40.00 1.27
50.00 1.42
60.00 1.55
70.00 1.70
80.00 1.76
90.00 1.90
100.00 2.01
3、数据记录与处理
周期二次方(s2)
摆长(cm) 周期(s)
①
②
③
④
⑤
⑥
⑦
⑧
⑨
20.00 0.90
30.00 1.10
40.00 1.27
50.00 1.42
60.00 1.55
70.00 1.70
80.00 1.76
90.00 1.90
100.00 2.01
0.81
1.21
1.61
2.02
2.40
2.89
3.10
3.61
4.04
实验结论:单摆周期的二次方与摆长成正比
秋千
风铃
吊灯
摆钟
摆钟
惠更斯摆钟
伽利略
惠更斯
§1.2 单摆
一、单摆(理想化的模型)
1、定义:忽略悬挂小球的细线长度的微小变化和质量,且线长比球的直径大得多,这样的装置就叫单摆.
2、单摆的结构:
①固定悬点O’
θ
②摆长l:悬点到重心的距离
l
③θ :最大摆角
B
C
想一想:下列装置能否看作单摆?
?
受力分析?
θ
C
拉力和重力沿半径的分力G2 提供向心力
重力的切线分力G1使摆球回 到平衡位置
提供回复力
摆球下摆的过程中,向心力、绳子拉力、回复力分别如何变化?
T=mgcosθ+ mv2/L
θ减小,v增大,向心力增大,T增大
最高点: V= 0 向心力为0
Tmin=mgcosθ F回max=mgsinθ
最低点:θ=0 速度最大,向心力最大
Tmax= mg+ mv2/L F回min=0
当最大偏角很小时(θ < 5°),
即:sinα≈α
Sin5°=0.08716
5°=5π/180=0.08727
此时,
即:
sinα≈
此时,位移x与G1近似平行
重力沿切线分力G1跟位移方向相反吗?
跟位移大小有什么关系?
结论:在偏角θ< 5°情况下,单摆的振动是简谐运动
二、单摆做简谐运动的周期
重力
加速度
猜想: 单摆振动的周期与哪些因素有关呢?
控制变量法
伽利略18岁时,到教堂做礼拜,他发现吊灯摆动的幅度虽然慢慢地在变小,但摆动一次所用时间却没有变化。他用自己的脉搏的跳动次数来测算。终于肯定了吊灯摆动周期与摆动的幅度无关这个单摆摆动的等时性规律。后来他利用这个原理制成了一个 “脉搏计”,帮助判断病人患病的情况。
实验证明:(在重力加速度g不变时)
单摆振动周期与小球质量,振幅无关,与摆长有关;摆长越长,周期越长。
周期公式:
单摆做简谐运动的振动周期跟摆长的平方根成正比,跟重力加速度的平方根成反比。
1、计时器:惠更斯于1656年发明了世界上第一个用摆的等时性来计时的时钟。(1657年获得专利权)
三、单摆周期公式的应用
注意:无论快钟,慢钟,标准钟每摆动一次,指示的时间是相同的。
哈尔滨人在香港买的摆钟,到家后发现走时不准的原因是什么?是变慢了还是变快了?应该如何调整?
学以致用:
摆钟:利用单摆的等时性计时,摆的周期可通过改变摆长来调节.周期为2s摆长为1m的单摆叫秒摆.
2、 用单摆测定重力加速度
开动脑筋:
如果你在一座高山的山顶,你能用单摆测山的海拔高度吗?如果可以,还需要什么仪器?
(已知地球质量及地球平均半径)
实验:探究周期T与摆长L的关系
操作:
1、测摆长
2、测周期
实验:探究周期T与摆长L的关系
累积法测单摆周期:振动稳定后,小球某次经过平衡位置时开始计时并数“0”,再经过平衡位置数“1”,数到“n”停止计时,测出总时间t,求出周期的平均值T,T=t/2n
机械秒表使用:按动中间按钮启动计时,再按动按钮停止计时,按左侧按钮清零。
机械秒表读数:
长针:一圈30s,最小刻度0.1s,不估读
短针:一圈15min,最小刻度0.5min,不估读
电子秒表使用:按动中间按钮使显示屏显示如图,进入计时功能。按动右侧按钮开始计时,再按动右侧按钮停止计时,从显示屏直接读数。按动左侧按钮清零。
实验:探究周期T与摆长L的关系
实验:探究周期T与摆长L的关系
3.数据记录与处理
摆长(m) 30次振动时间(s) 周期(s)
① 0.2
② 0.4
③ 0.6
④ 0.8
⑤ 1.0
3、数据记录与处理
摆长(cm) 周期(s)
①
②
③
④
⑤
⑥
⑦
⑧
⑨
20.00 0.90
30.00 1.10
40.00 1.27
50.00 1.42
60.00 1.55
70.00 1.70
80.00 1.76
90.00 1.90
100.00 2.01
3、数据记录与处理
周期二次方(s2)
摆长(cm) 周期(s)
①
②
③
④
⑤
⑥
⑦
⑧
⑨
20.00 0.90
30.00 1.10
40.00 1.27
50.00 1.42
60.00 1.55
70.00 1.70
80.00 1.76
90.00 1.90
100.00 2.01
0.81
1.21
1.61
2.02
2.40
2.89
3.10
3.61
4.04
实验结论:单摆周期的二次方与摆长成正比
同课章节目录
- 第一章 机械振动
- 1 简谐运动
- 2 单摆
- 3 简谐运动的图像和公式
- 4 阻尼振动 受迫振动
- 5 实验探究:用单摆测定重力加速度
- 第二章 机械波
- 1 机械波的形成和传播
- 2 横波的图像
- 3 波的频率和波速
- 4 惠更新原理 波的反射与折射
- 5 波的干射 衍射
- 6 多普勒效应
- 第三章 电磁振荡 电磁波
- 1 电磁振荡
- 2 电磁场和电磁波
- 3 电磁波谱 电磁波的应用
- 4 无线电波的发射、传播和接收
- 第四章 光的折射
- 1 光的折射定律
- 2 实验探究:测定玻璃的折射率
- 3 光的全反射
- 第五章 光的波动性
- 1 光的干涉
- 2 实验探究:用双缝干涉油光的波长
- 3 光的衍射与偏振
- 4 激光
- 第六章 相对论
- 1 经典时空观
- 2 狭义对相对论的两个基本假设
- 3 相对论时空观
- 4 相对论的速度变换定律 质量和能量的关系
- 5 广义相对论
