苏科版数学八下 9.1 图形的旋转 课件(20张)
文档属性
| 名称 | 苏科版数学八下 9.1 图形的旋转 课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-30 15:06:06 | ||
图片预览





文档简介
(共20张PPT)
图形的旋转
数学
创设情境
平移
翻折
旋转
旋转
操作探究
B
A
C
E
D
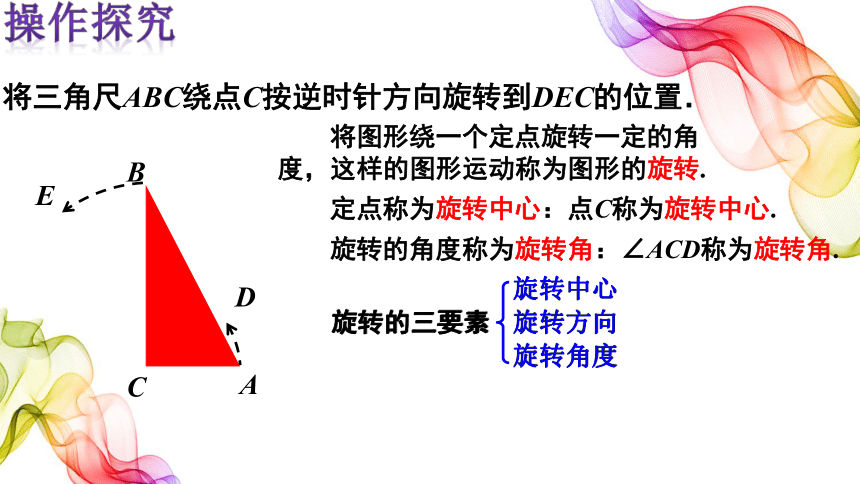
将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.
将图形绕一个定点旋转一定的角度,这样的图形运动称为图形的旋转.
旋转的角度称为旋转角:∠ACD称为旋转角.
定点称为旋转中心:点C称为旋转中心.
旋转的三要素
旋转中心
旋转方向
旋转角度
操作探究
B
A
C
E
D
将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.
点A绕点C旋转到点D,点A与点D称为对应点.
边AC绕点C旋转到边DC,AC与DC称为对应边.
∠A绕点C旋转到∠D, ∠A与∠D称为对应角.
操作探究
B
A
C
E
D
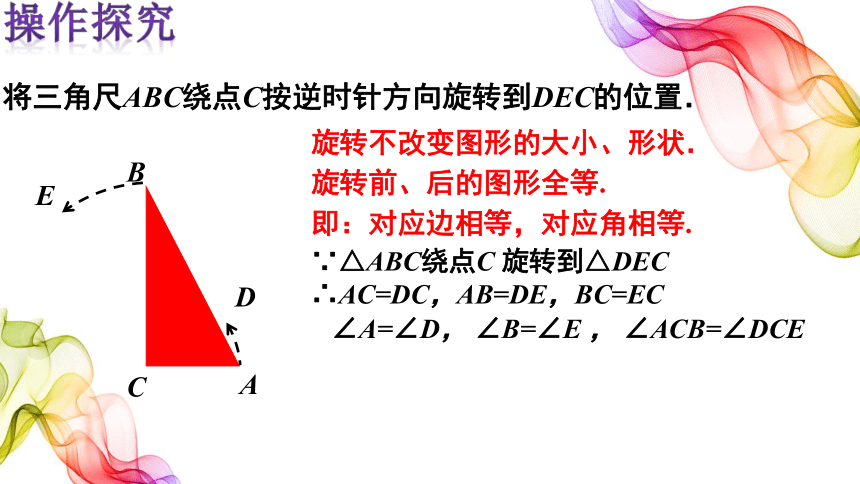
将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.
∵△ABC绕点C 旋转到△DEC∴AC=DC,AB=DE,BC=EC
∠A=∠D, ∠B=∠E , ∠ACB=∠DCE
旋转不改变图形的大小、形状.
旋转前、后的图形全等.
即:对应边相等,对应角相等.
线段AB的对应线段是线段___;
∠A的对应角是 ;
∠B的对应角是 ;
旋转中心是点 ;
旋转的角是 .
线段OB的对应线段是线段___;
点B的对应点是点 ;
∠D
∠E
O
45?
E
OE
DE
E
D
O
A
B
如图,△DOE是△AOB绕点O按顺时针方向旋转45°所得的.
练一练
操作探究
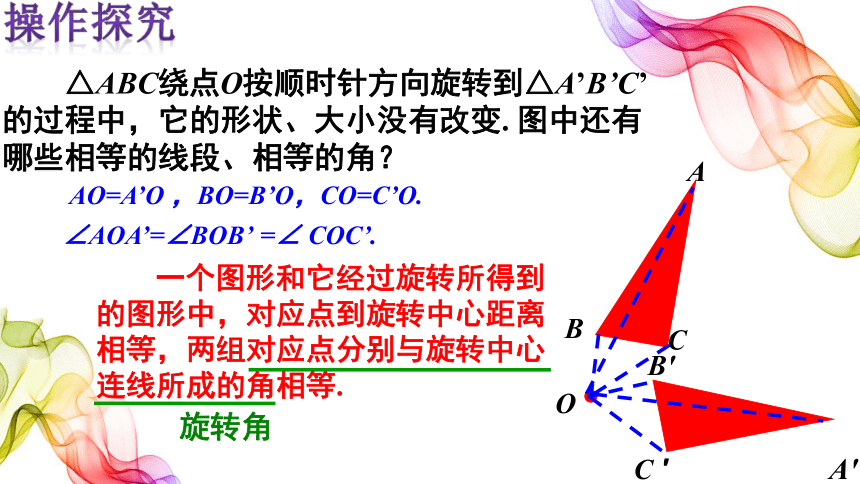
△ABC绕点O按顺时针方向旋转到△A’B’C’的过程中,它的形状、大小没有改变. 图中还有哪些相等的线段、相等的角?
O
C
A
B
C '
A'
B'
AO=A’O ,BO=B’O,CO=C’O.
∠AOA’=∠BOB’ =∠ COC’.
一个图形和它经过旋转所得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等.
旋转角
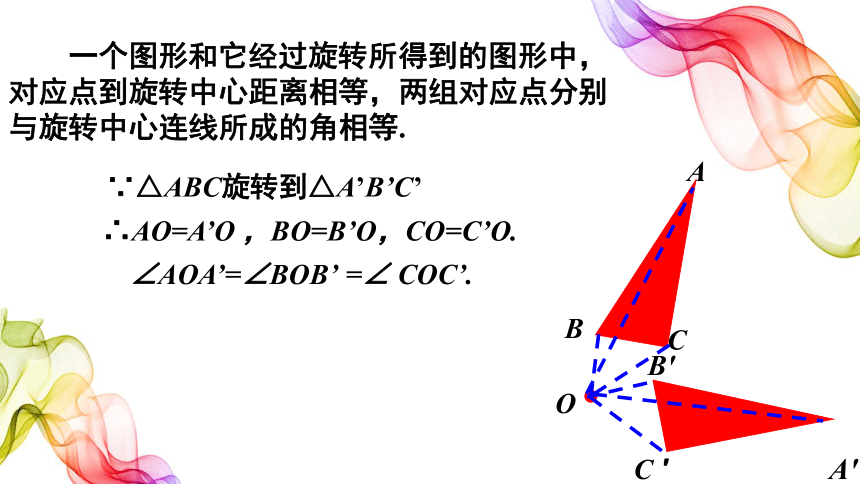
∵△ABC旋转到△A’B’C’
O
C
A
B
C '
A'
B'
∴AO=A’O ,BO=B’O,CO=C’O.
∠AOA’=∠BOB’ =∠ COC’.
一个图形和它经过旋转所得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等.
图形旋转的性质:
1.旋转前、后图形的大小、形状不变.
即:旋转前、后图形全等.
2.一个图形和它经过旋转所得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等.
知识应用
例1.
画出将点A绕点O按顺时针方向旋转100°后的点A'.
A?
C
A
O
(2)在射线OC上截取OA'=OA,则点A'
就是所要画的点.
(1)连接OA,以O为顶点、 OA为一边
作∠AOC=100°;
作法:
知识应用
例2.
画出将线段AB绕点O按顺时针方向旋转100°后的图形.
O
A
B
A?
B?
C
(3)连接A ’ B’,则线段A’B’即为所求.
(1)连接OA,作∠AOC=100°, 在射线OC上截取OA'=OA;
(2)连接OB,作∠BOD=100°,在射线OD上截取OB'=OB;
作法:
D
知识应用
例3.
画出将△ABC绕点O按顺时针方向旋转100°后的对应三角形.
A
O
C
B
A?
C?
B?
画一个图形绕一个点旋转后所得的图形,关键是确定某些点绕这个点旋转后所得到的对应点.
画一个多边形绕着某点旋转一定角度后的图形, 首先画出各个顶点绕着某点旋转一定角度后的对应顶点,然后依次连接各个对应顶点.
所以△A’B’C’即为所求.
知识应用
例4.如图,如果线段MO绕点O旋转90O,得到线段NO,在这个旋转过程中,旋转中心是 ,旋转角是 ,它是 度.
M
O
N
O
∠MON
90
知识应用
例5.如图,△ABC与△BDE都是等腰直角三角形,∠ACB和∠E都是直角,若△ABC经旋转后能与△BDE重合,那么旋转中心是 ,旋转了 度.
点B
45
知识应用
例6.如图,在正方形ABCD中,E是CB延长线上一点,
(1) 旋转中心是哪一点?
(2) ∠EAF是多少度?
A
B
F
C
E
D
(3) 如果点G是AB的中点,那么经过上述旋转后,点G到什么位置?请在图中将点G的对应点G'表示出来.
G
△ABE经过旋转后得到△ADF. 请按图回答:
点A
90°
旋转后点G到了AD的中点G’.
G’
知识应用
例7.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55°
B.60°
C.65°
D.70°
解:
∵Rt△ABC绕直角顶点C顺时针
旋转90°得到△A′B′C,
∴AC=A′C,
∴△ACA′是等腰直角三角形,
∴∠CA′A=45°,∠CA′B′=20°=∠BAC
∴∠BAA′=180°﹣70°﹣45°=65°.
故选:C.
C
知识应用
例8.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
A.4
B.3
C.2
D.1
解:如图连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4,
根据旋转不变性可知,A′B′=AB=4,
∴A′P=PB′,
∴PC=
0.5A′B′=2,
∵CM=BM=1,
又∵PM≤PC+CM,即PM≤3,
∴PM的最大值为3(此时P、C、M共线).
故选B.
B
感悟交流
1.从熟悉的生活中的旋转现象出发,探究出在平面内,将图形绕一个定点旋转一定的角度,这样的图形运动称为图形的旋转.知道了图形的旋转是由旋转中心、旋转角度和旋转方向决定.
2.图形旋转的性质:
(1)旋转不改变图形的大小、形状,即旋转前、后的图形全等.
(2)对应点到旋转中心的距离相等.
(3)每一对对应点与旋转中心的连线所成的角相等.
3.画一个图形绕着一个点旋转一定角度后的图形,先画出各顶点旋转后的对应顶点,然后按一定的顺序连接各个对应顶点.
布置作业
1.养成预习的好习惯.
2.回忆本节课的主要内容,复习笔记.
3.完成《图形的旋转》课后检测.
图形的旋转
数学
创设情境
平移
翻折
旋转
旋转
操作探究
B
A
C
E
D
将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.
将图形绕一个定点旋转一定的角度,这样的图形运动称为图形的旋转.
旋转的角度称为旋转角:∠ACD称为旋转角.
定点称为旋转中心:点C称为旋转中心.
旋转的三要素
旋转中心
旋转方向
旋转角度
操作探究
B
A
C
E
D
将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.
点A绕点C旋转到点D,点A与点D称为对应点.
边AC绕点C旋转到边DC,AC与DC称为对应边.
∠A绕点C旋转到∠D, ∠A与∠D称为对应角.
操作探究
B
A
C
E
D
将三角尺ABC绕点C按逆时针方向旋转到DEC的位置.
∵△ABC绕点C 旋转到△DEC∴AC=DC,AB=DE,BC=EC
∠A=∠D, ∠B=∠E , ∠ACB=∠DCE
旋转不改变图形的大小、形状.
旋转前、后的图形全等.
即:对应边相等,对应角相等.
线段AB的对应线段是线段___;
∠A的对应角是 ;
∠B的对应角是 ;
旋转中心是点 ;
旋转的角是 .
线段OB的对应线段是线段___;
点B的对应点是点 ;
∠D
∠E
O
45?
E
OE
DE
E
D
O
A
B
如图,△DOE是△AOB绕点O按顺时针方向旋转45°所得的.
练一练
操作探究
△ABC绕点O按顺时针方向旋转到△A’B’C’的过程中,它的形状、大小没有改变. 图中还有哪些相等的线段、相等的角?
O
C
A
B
C '
A'
B'
AO=A’O ,BO=B’O,CO=C’O.
∠AOA’=∠BOB’ =∠ COC’.
一个图形和它经过旋转所得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等.
旋转角
∵△ABC旋转到△A’B’C’
O
C
A
B
C '
A'
B'
∴AO=A’O ,BO=B’O,CO=C’O.
∠AOA’=∠BOB’ =∠ COC’.
一个图形和它经过旋转所得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等.
图形旋转的性质:
1.旋转前、后图形的大小、形状不变.
即:旋转前、后图形全等.
2.一个图形和它经过旋转所得到的图形中,对应点到旋转中心距离相等,两组对应点分别与旋转中心连线所成的角相等.
知识应用
例1.
画出将点A绕点O按顺时针方向旋转100°后的点A'.
A?
C
A
O
(2)在射线OC上截取OA'=OA,则点A'
就是所要画的点.
(1)连接OA,以O为顶点、 OA为一边
作∠AOC=100°;
作法:
知识应用
例2.
画出将线段AB绕点O按顺时针方向旋转100°后的图形.
O
A
B
A?
B?
C
(3)连接A ’ B’,则线段A’B’即为所求.
(1)连接OA,作∠AOC=100°, 在射线OC上截取OA'=OA;
(2)连接OB,作∠BOD=100°,在射线OD上截取OB'=OB;
作法:
D
知识应用
例3.
画出将△ABC绕点O按顺时针方向旋转100°后的对应三角形.
A
O
C
B
A?
C?
B?
画一个图形绕一个点旋转后所得的图形,关键是确定某些点绕这个点旋转后所得到的对应点.
画一个多边形绕着某点旋转一定角度后的图形, 首先画出各个顶点绕着某点旋转一定角度后的对应顶点,然后依次连接各个对应顶点.
所以△A’B’C’即为所求.
知识应用
例4.如图,如果线段MO绕点O旋转90O,得到线段NO,在这个旋转过程中,旋转中心是 ,旋转角是 ,它是 度.
M
O
N
O
∠MON
90
知识应用
例5.如图,△ABC与△BDE都是等腰直角三角形,∠ACB和∠E都是直角,若△ABC经旋转后能与△BDE重合,那么旋转中心是 ,旋转了 度.
点B
45
知识应用
例6.如图,在正方形ABCD中,E是CB延长线上一点,
(1) 旋转中心是哪一点?
(2) ∠EAF是多少度?
A
B
F
C
E
D
(3) 如果点G是AB的中点,那么经过上述旋转后,点G到什么位置?请在图中将点G的对应点G'表示出来.
G
△ABE经过旋转后得到△ADF. 请按图回答:
点A
90°
旋转后点G到了AD的中点G’.
G’
知识应用
例7.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55°
B.60°
C.65°
D.70°
解:
∵Rt△ABC绕直角顶点C顺时针
旋转90°得到△A′B′C,
∴AC=A′C,
∴△ACA′是等腰直角三角形,
∴∠CA′A=45°,∠CA′B′=20°=∠BAC
∴∠BAA′=180°﹣70°﹣45°=65°.
故选:C.
C
知识应用
例8.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
A.4
B.3
C.2
D.1
解:如图连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4,
根据旋转不变性可知,A′B′=AB=4,
∴A′P=PB′,
∴PC=
0.5A′B′=2,
∵CM=BM=1,
又∵PM≤PC+CM,即PM≤3,
∴PM的最大值为3(此时P、C、M共线).
故选B.
B
感悟交流
1.从熟悉的生活中的旋转现象出发,探究出在平面内,将图形绕一个定点旋转一定的角度,这样的图形运动称为图形的旋转.知道了图形的旋转是由旋转中心、旋转角度和旋转方向决定.
2.图形旋转的性质:
(1)旋转不改变图形的大小、形状,即旋转前、后的图形全等.
(2)对应点到旋转中心的距离相等.
(3)每一对对应点与旋转中心的连线所成的角相等.
3.画一个图形绕着一个点旋转一定角度后的图形,先画出各顶点旋转后的对应顶点,然后按一定的顺序连接各个对应顶点.
布置作业
1.养成预习的好习惯.
2.回忆本节课的主要内容,复习笔记.
3.完成《图形的旋转》课后检测.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
