苏科版数学八下 9.2 中心对称与中心对称图形 课件(24张)
文档属性
| 名称 | 苏科版数学八下 9.2 中心对称与中心对称图形 课件(24张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-30 15:09:32 | ||
图片预览






文档简介
(共24张PPT)
中心对称与
中心对称图形
数学
温故知新
1.将图形绕一个定点旋转一定的角度,这样的图形运动称为图形的旋转.知道了图形的旋转是由旋转中心、旋转角度和旋转方向决定.
2.图形旋转的性质:
(1)旋转不改变图形的大小、形状,即旋转前、后的图形全等.
(2)对应点到旋转中心的距离相等.
(3)每一对对应点与旋转中心的连线所成的角相等.
温故知新
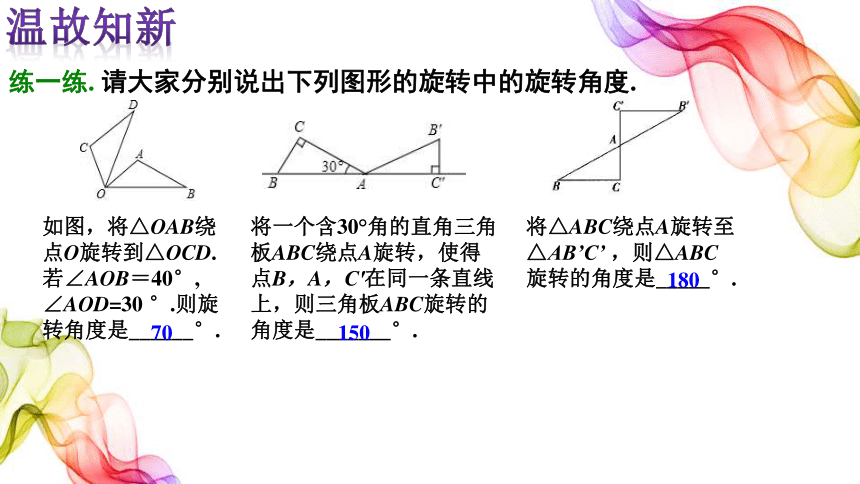
练一练. 请大家分别说出下列图形的旋转中的旋转角度.
将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是_______°.
150
如图,将△OAB绕点O旋转到△OCD.若∠AOB=40°,
∠AOD=30 °.则旋转角度是______°.
70
将△ABC绕点A旋转至△AB’C’ ,则△ABC旋转的角度是_____°.
180
问题引入
“双鱼”剪纸作品是由两个形状、大小完全形同的图案组成的.
“双鼠”剪纸作品是由两个形状、大小完全形同的图案组成的.
共性:将其中的一个图形绕着某一点旋转180°能够与另一个图形重合.
操作探究
O
A
B
C
D
E
F
A
B
C
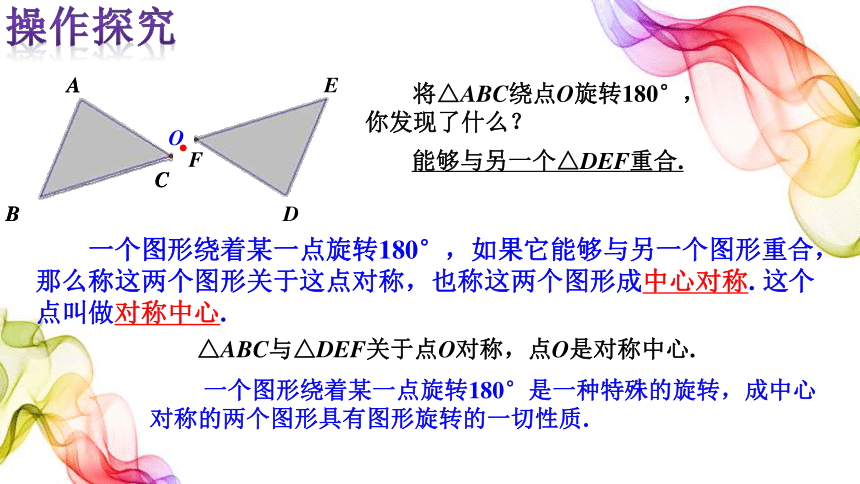
将△ABC绕点O旋转180°,你发现了什么?
能够与另一个△DEF重合.
一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称. 这个点叫做对称中心.
△ABC与△DEF关于点O对称,点O是对称中心.
一个图形绕着某一点旋转180°是一种特殊的旋转,成中心对称的两个图形具有图形旋转的一切性质.
操作探究
△ABC与△DEF关于点O对称,点O是对称中心.
图形旋转的性质:
(1)旋转前、后图形全等.
(2)对应点到旋转中心的距离相等.
(3)每一对对应点与旋转中心的连线所成的角相等.
△ABC≌△DEF
OA=OD,OB=OE,OC=OF
∠AOD=∠BOE=∠COF=180°
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
归纳性质
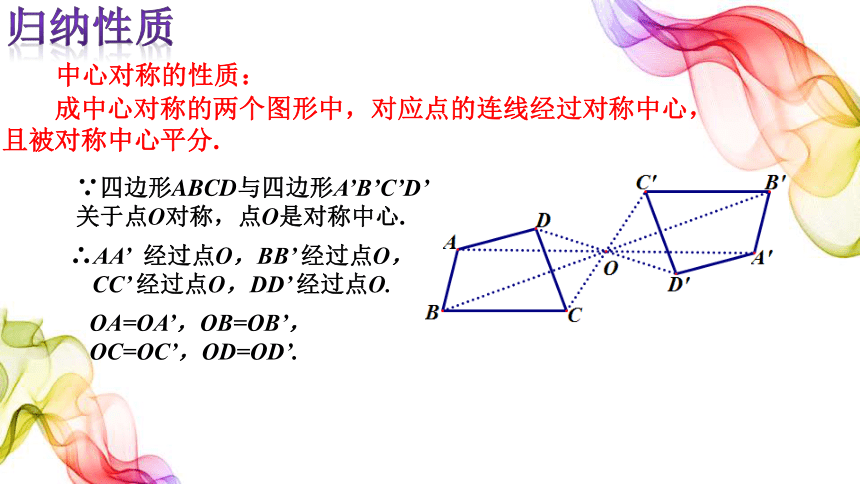
中心对称的性质:
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
∵四边形ABCD与四边形A’B’C’D’关于点O对称,点O是对称中心.
OA=OA’,OB=OB’,OC=OC’,OD=OD’.
∴AA’ 经过点O,BB’ 经过点O, CC’ 经过点O,DD’ 经过点O.
1.下列说法正确的是( )
A.两个能够互相重合的图形一定成中心对称.
B.成中心对称的两个图形一定能够互相重合.
C.把一个图形绕着某一点旋转一定的角度,如果它能够与另一个图形重合,那么这两个图形一定成中心对称.
D.如果两个图形的对应点连线都经过某一点,那么这两个图形关于这一点成中心对称.
B
知识辨析
知识辨析
2.若两个图形成中心对称,则下列说法:①对称点的连线必过对称中心;②这两个图形的形状和大小完全相同;③这两个图形的对应线段一定互相平行;④将一个图形围绕对称中心旋转某个角度后必与另一个图形重合.其中正确的有( )
A.1个 B.2个 C.3个 D. 4个
B
对应点
知识运用
例1.如图,画出点A关于点O对称的点.
.
.
A
O
.
A′
(2)则点A′ 即为所求.
(1)连接AO,并延长到点A’,使得OA’=OA;
作法:
知识运用
例2.如图,画出线段AB关于点O对称的线段.
(3)连接A’B’,则线段A’B’即为所求.
(1)连接AO,并延长到点A’,使得OA’=OA;
作法:
A
B
.
O
(2)连接BO,并延长到点B’,使得OB’=OB;
·
A’
·
B’
知识运用
例3.如图,画出△ABC关于点O对称的三角形.
(4)依次连接A’B’C’,则△A’B’C’即为所求.
(1)连接AO,并延长到点A’,使得OA’=OA;
作法:
(2)连接BO,并延长到点B’,使得OB’=OB;
(3)连接CO,并延长到点C’,使得OC’=OC;
·
A’
·
B’
·
C’
知识运用
例4.在平面直角坐标系中,△ABC的三个顶点坐标分别为
A(-2, 1)、B(-4, 5)、C(-5, 2) .
(1)画出△ABC关于原点成中心对称的△DEF;
(2)分别写出△DEF三个顶点的坐标;
并判断这三个顶点的坐标与△ABC
三个顶点的坐标有什么关系?
∴ △DEF即为所求.
D(2, -1)、E(4, -5)、F(5, -2)
D、E、F三个点的横、纵坐标分别与
A、B、C三个点的横、纵坐标互为相反数.
D、E、F三个点分别与
A、B、C三个点关于原点对称.
知识运用
例5.如图,两块同样的三角尺,它们是否关于某点成中 心对称?若是,请确定对称中心的位置.
A
∴ 点A就是对称中心.
操作探究
观察下列图案说一说它们有什么共同特征?
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形互相重合,那么这个图形叫做中心对称图形. 这个点就是它的对称中心.
巩固练习
1. 下列美丽的图案中,中心对称图形有( )
A.1个 B.2个 C.3个 D.4个
90°
180°
270°
120°
240°
60° 120°
180°240°
300°
90°
180°
270°
C
2.观察图形,并回答下面的问题:
(1)哪些是轴对称图形?
(2)哪些是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(1) (2) (3) (4) (5)
(1)、(2)、(3)、(4)、(5)
(1)、 (4)
(1)、 (4)
巩固练习
感悟交流
若把成中心对称的两个图形看作一个整体,则成为中心对称图形.
感悟交流
中心对称与中心对称图形有什么区别与联系?
名称 中心对称 中心对称图形
定义 一个图形绕着某一点旋转180?,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称,这个点叫做对称中心. 把一个图形绕某一点旋转180?,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
性质 ①两个图形可完全重合;
②对应点的连线经过对称中心,且被对称中心平分. ①是一个特殊的图形;
②对应点的连线经过对称中心,且被对称中心平分.
区别 ①两个图形的关系;
②对称点在两个图形上. ①具有某种性质的一个图形;
②对称点在一个图形上.
联系 若把中心对称图形的两部分分别看作两个图形,则它们成中心对称.
若把中心对称的两个图形看作一个整体,则成为中心对称图形.
巩固练习
3.判断题:
①如果两个图形关于某点成中心对称,那么这两个图形全等. ( )
②两个全等的图形一定关于某点成中心对称. ( )
③如果两个图形关于某点成中心对称,那么将其中一个图形
绕着对称中心旋转180°必定与另一个图形重合. ( )
④如果两个图形关于某点成中心对称,那么对称点的连线
一定经过对称中心. ( )
√
×
√
√
课堂小结
1.中心对称与中心对称图形的定义.
2.中心对称与中心对称图形的性质.
3.中心对称与中心对称图形的区别与联系.
课堂小结
1. 利用图形旋转的性质归纳得出中心对称的性质,有意识的培养自己演绎推理的能力和独立思考的习惯.
2.注重探究的过程,在得出中心对称的性质时,先充分思考,再研究图形,最后得出结论,动手动脑.
3.注意加强操作训练,会画草图,能整体把握图形的意识;最后通过正规作图,养成良好的作图习惯.
布置作业
完成《中心对称与中心对称图形》课后检测.
对称美是数学美的重要部分。
哥白尼说:“在这种有条不紊的安排之下,宇宙中存在着奇妙的对称……”.对称是广义的,字母的对称,结构的对称,图形的对称,解法的对称……
无论哪种对称,都是美好的.
中心对称与
中心对称图形
数学
温故知新
1.将图形绕一个定点旋转一定的角度,这样的图形运动称为图形的旋转.知道了图形的旋转是由旋转中心、旋转角度和旋转方向决定.
2.图形旋转的性质:
(1)旋转不改变图形的大小、形状,即旋转前、后的图形全等.
(2)对应点到旋转中心的距离相等.
(3)每一对对应点与旋转中心的连线所成的角相等.
温故知新
练一练. 请大家分别说出下列图形的旋转中的旋转角度.
将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是_______°.
150
如图,将△OAB绕点O旋转到△OCD.若∠AOB=40°,
∠AOD=30 °.则旋转角度是______°.
70
将△ABC绕点A旋转至△AB’C’ ,则△ABC旋转的角度是_____°.
180
问题引入
“双鱼”剪纸作品是由两个形状、大小完全形同的图案组成的.
“双鼠”剪纸作品是由两个形状、大小完全形同的图案组成的.
共性:将其中的一个图形绕着某一点旋转180°能够与另一个图形重合.
操作探究
O
A
B
C
D
E
F
A
B
C
将△ABC绕点O旋转180°,你发现了什么?
能够与另一个△DEF重合.
一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称. 这个点叫做对称中心.
△ABC与△DEF关于点O对称,点O是对称中心.
一个图形绕着某一点旋转180°是一种特殊的旋转,成中心对称的两个图形具有图形旋转的一切性质.
操作探究
△ABC与△DEF关于点O对称,点O是对称中心.
图形旋转的性质:
(1)旋转前、后图形全等.
(2)对应点到旋转中心的距离相等.
(3)每一对对应点与旋转中心的连线所成的角相等.
△ABC≌△DEF
OA=OD,OB=OE,OC=OF
∠AOD=∠BOE=∠COF=180°
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
归纳性质
中心对称的性质:
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心平分.
∵四边形ABCD与四边形A’B’C’D’关于点O对称,点O是对称中心.
OA=OA’,OB=OB’,OC=OC’,OD=OD’.
∴AA’ 经过点O,BB’ 经过点O, CC’ 经过点O,DD’ 经过点O.
1.下列说法正确的是( )
A.两个能够互相重合的图形一定成中心对称.
B.成中心对称的两个图形一定能够互相重合.
C.把一个图形绕着某一点旋转一定的角度,如果它能够与另一个图形重合,那么这两个图形一定成中心对称.
D.如果两个图形的对应点连线都经过某一点,那么这两个图形关于这一点成中心对称.
B
知识辨析
知识辨析
2.若两个图形成中心对称,则下列说法:①对称点的连线必过对称中心;②这两个图形的形状和大小完全相同;③这两个图形的对应线段一定互相平行;④将一个图形围绕对称中心旋转某个角度后必与另一个图形重合.其中正确的有( )
A.1个 B.2个 C.3个 D. 4个
B
对应点
知识运用
例1.如图,画出点A关于点O对称的点.
.
.
A
O
.
A′
(2)则点A′ 即为所求.
(1)连接AO,并延长到点A’,使得OA’=OA;
作法:
知识运用
例2.如图,画出线段AB关于点O对称的线段.
(3)连接A’B’,则线段A’B’即为所求.
(1)连接AO,并延长到点A’,使得OA’=OA;
作法:
A
B
.
O
(2)连接BO,并延长到点B’,使得OB’=OB;
·
A’
·
B’
知识运用
例3.如图,画出△ABC关于点O对称的三角形.
(4)依次连接A’B’C’,则△A’B’C’即为所求.
(1)连接AO,并延长到点A’,使得OA’=OA;
作法:
(2)连接BO,并延长到点B’,使得OB’=OB;
(3)连接CO,并延长到点C’,使得OC’=OC;
·
A’
·
B’
·
C’
知识运用
例4.在平面直角坐标系中,△ABC的三个顶点坐标分别为
A(-2, 1)、B(-4, 5)、C(-5, 2) .
(1)画出△ABC关于原点成中心对称的△DEF;
(2)分别写出△DEF三个顶点的坐标;
并判断这三个顶点的坐标与△ABC
三个顶点的坐标有什么关系?
∴ △DEF即为所求.
D(2, -1)、E(4, -5)、F(5, -2)
D、E、F三个点的横、纵坐标分别与
A、B、C三个点的横、纵坐标互为相反数.
D、E、F三个点分别与
A、B、C三个点关于原点对称.
知识运用
例5.如图,两块同样的三角尺,它们是否关于某点成中 心对称?若是,请确定对称中心的位置.
A
∴ 点A就是对称中心.
操作探究
观察下列图案说一说它们有什么共同特征?
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形互相重合,那么这个图形叫做中心对称图形. 这个点就是它的对称中心.
巩固练习
1. 下列美丽的图案中,中心对称图形有( )
A.1个 B.2个 C.3个 D.4个
90°
180°
270°
120°
240°
60° 120°
180°240°
300°
90°
180°
270°
C
2.观察图形,并回答下面的问题:
(1)哪些是轴对称图形?
(2)哪些是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(1) (2) (3) (4) (5)
(1)、(2)、(3)、(4)、(5)
(1)、 (4)
(1)、 (4)
巩固练习
感悟交流
若把成中心对称的两个图形看作一个整体,则成为中心对称图形.
感悟交流
中心对称与中心对称图形有什么区别与联系?
名称 中心对称 中心对称图形
定义 一个图形绕着某一点旋转180?,如果它能够与另一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成中心对称,这个点叫做对称中心. 把一个图形绕某一点旋转180?,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
性质 ①两个图形可完全重合;
②对应点的连线经过对称中心,且被对称中心平分. ①是一个特殊的图形;
②对应点的连线经过对称中心,且被对称中心平分.
区别 ①两个图形的关系;
②对称点在两个图形上. ①具有某种性质的一个图形;
②对称点在一个图形上.
联系 若把中心对称图形的两部分分别看作两个图形,则它们成中心对称.
若把中心对称的两个图形看作一个整体,则成为中心对称图形.
巩固练习
3.判断题:
①如果两个图形关于某点成中心对称,那么这两个图形全等. ( )
②两个全等的图形一定关于某点成中心对称. ( )
③如果两个图形关于某点成中心对称,那么将其中一个图形
绕着对称中心旋转180°必定与另一个图形重合. ( )
④如果两个图形关于某点成中心对称,那么对称点的连线
一定经过对称中心. ( )
√
×
√
√
课堂小结
1.中心对称与中心对称图形的定义.
2.中心对称与中心对称图形的性质.
3.中心对称与中心对称图形的区别与联系.
课堂小结
1. 利用图形旋转的性质归纳得出中心对称的性质,有意识的培养自己演绎推理的能力和独立思考的习惯.
2.注重探究的过程,在得出中心对称的性质时,先充分思考,再研究图形,最后得出结论,动手动脑.
3.注意加强操作训练,会画草图,能整体把握图形的意识;最后通过正规作图,养成良好的作图习惯.
布置作业
完成《中心对称与中心对称图形》课后检测.
对称美是数学美的重要部分。
哥白尼说:“在这种有条不紊的安排之下,宇宙中存在着奇妙的对称……”.对称是广义的,字母的对称,结构的对称,图形的对称,解法的对称……
无论哪种对称,都是美好的.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
