中考数学二轮专题复习图形变换——旋转问题(PDF版,附答案)
文档属性
| 名称 | 中考数学二轮专题复习图形变换——旋转问题(PDF版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 414.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 14:34:43 | ||
图片预览



文档简介
二轮复习:图形变换(二)———旋转
在解决旋转问题时,应注意旋转前后相对应的边相等、角相,旋转角度在计
算过程中的应用等。下面着重从三个方面进行讲述:三角形旋转、特殊平行四边
形旋转和在平面直角坐标系内的图形旋转三大类进行。
(一)三角形的旋转
题型 1、求角的度数
1、如图,在△ABC 中,∠CAB=75°,将△ABC 在平面内绕点 A 旋转到△AB′C′的位
置,使 CC′∥AB,则旋转角的度数为
A.30° B.40° C.50° D.75°
2、(2019?常德)如图,已知△ABC是等腰三角形,AB=AC,∠BAC=45°,点 D在 AC
边上,将△ABD绕点 A逆时针旋转 45°得到△ACD′,且点 D′、D、B三点在同一条直
线上,则∠ABD的度数是 .
题型 2、求线段的长度
3、(2019?新疆)如图,在△ABC中,AB=AC=4,将△ABC绕点 A顺时针旋转 30°,得
到△ACD,延长 AD交 BC的延长线于点 E,则 DE的长为 .
4、(2019?哈尔滨)如图,将△ABC绕点 C逆时针旋转得到△A′B′C,其中点 A′与 A是
对应点,点 B′与 B是对应点,点 B′落在边 AC上,连接 A′B,若∠ACB=45°,AC
=3,BC=2,则 A′B的长为 .
题型 3、求旋转重合的图形面积
5、如图,等腰直角三角形 ABC 的直角边 AB 的长为 6cm,将△ABC 绕点 A 逆时针旋转 15°后
得到△AB′C′,则图中阴影部分面积等于 cm
2
.
题型 4、特殊三角形的旋转
6、(2019 绵阳)如图,△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,
DE=2 �.将△BDE绕点 B逆时针方向旋转后得△BD′E′,当点 E′恰好落在线段 AD′上时,则
CE′=______.
7、(2019 眉山)如图,在 Rt△ABC中,∠B=900,AB=5,BC=12,将△ABC绕点 A逆时
针旋转得到△ADE,使得点 D落在 AC上,则 tan∠ECD的值为 .
B
A D C
E
(二)特殊平行四边形旋转
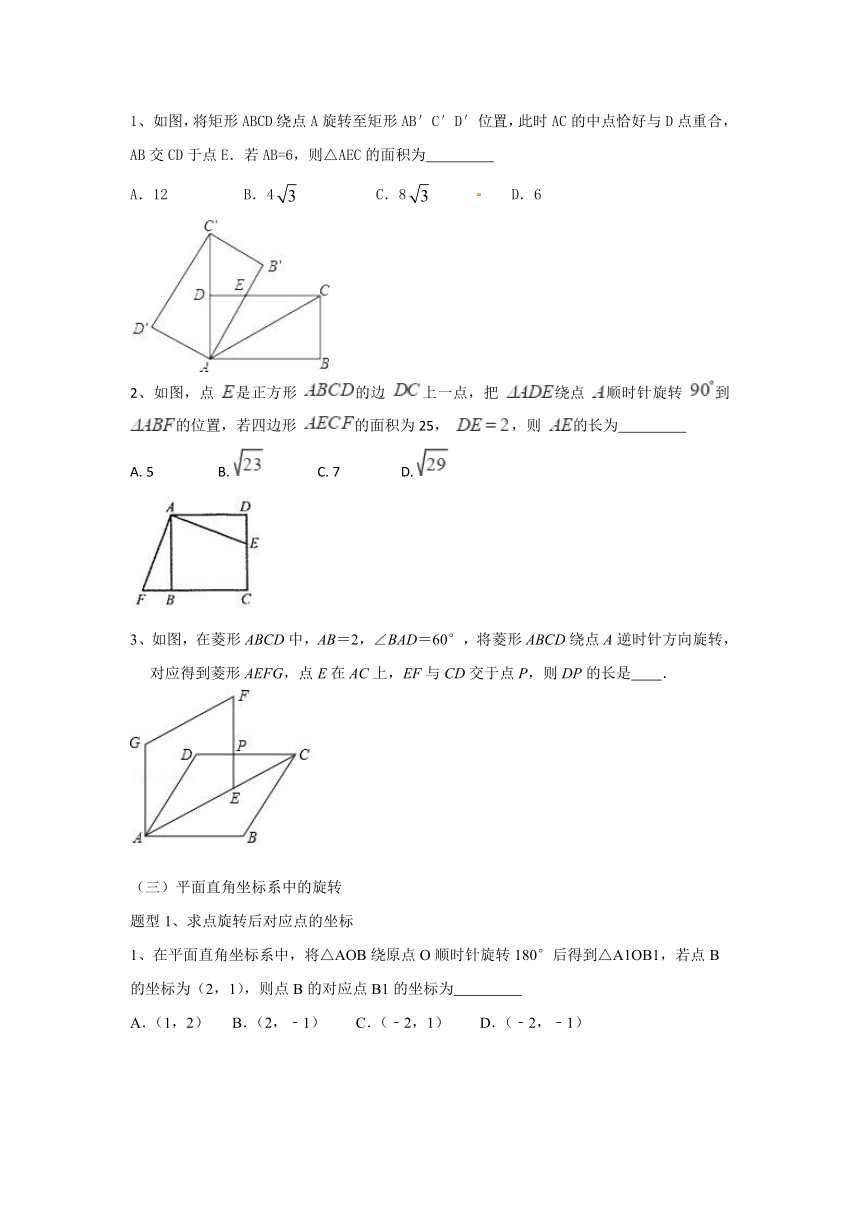
1、如图,将矩形 ABCD 绕点 A 旋转至矩形 AB′C′D′位置,此时 AC 的中点恰好与 D 点重合,
AB 交 CD 于点 E.若 AB=6,则△AEC 的面积为
A.12 B.4 3 C.8 3 D.6
2、如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到
的位置,若四边形 的面积为 25, ,则 的长为
A. 5 B. C. 7 D.
3、如图,在菱形 ABCD中,AB=2,∠BAD=60°,将菱形 ABCD绕点 A逆时针方向旋转,
对应得到菱形 AEFG,点 E在 AC上,EF与 CD交于点 P,则 DP的长是 .
(三)平面直角坐标系中的旋转
题型 1、求点旋转后对应点的坐标
1、在平面直角坐标系中,将△AOB绕原点 O顺时针旋转 180°后得到△A1OB1,若点 B
的坐标为(2,1),则点 B的对应点 B1 的坐标为
A.(1,2) B.(2,﹣1) C.(﹣2,1) D.(﹣2,﹣1)
2、如图,将线段 AB绕点 O顺时针旋转 90°得到线段 A′B′,那么 A(﹣2,5)的对应
点 A′的坐标是
A.(2,5) B.(5,2) C.(2,﹣5) D.(5,﹣2)
3、如图所示,在平面直角坐标系中,点 A、B的坐标分别为(-2,0)和(2,0).月牙①
绕点 B顺时针旋转 90°得到月牙②,则点 A的对应点 A′的坐标为
A.(2,2) B.(2,4) C.(4,2) D.(1,2)
题型 2、求三角形旋转后对应点的坐标
4、将含有 30°角的直角三角板 OAB如图放置在平面直角坐标系中,OB在 x轴上,若 OA=2,
将三角板绕原点 O顺时针旋转 75°,则点 A的对应点 A′的坐标为
A.( ,﹣1) B.(1,﹣ ) C.( ,﹣ ) D.(﹣ , )
5、将一个含 45°角的三角板 ABC如图摆放在平面直角坐标系中,将其绕点 C顺时针旋转
75°,点B的对应点B′恰好落在 x轴上,若点C的坐标为(1,0),则点B′的坐标为 .
题型 3、在函数图像中的点 旋转后对应点的坐标
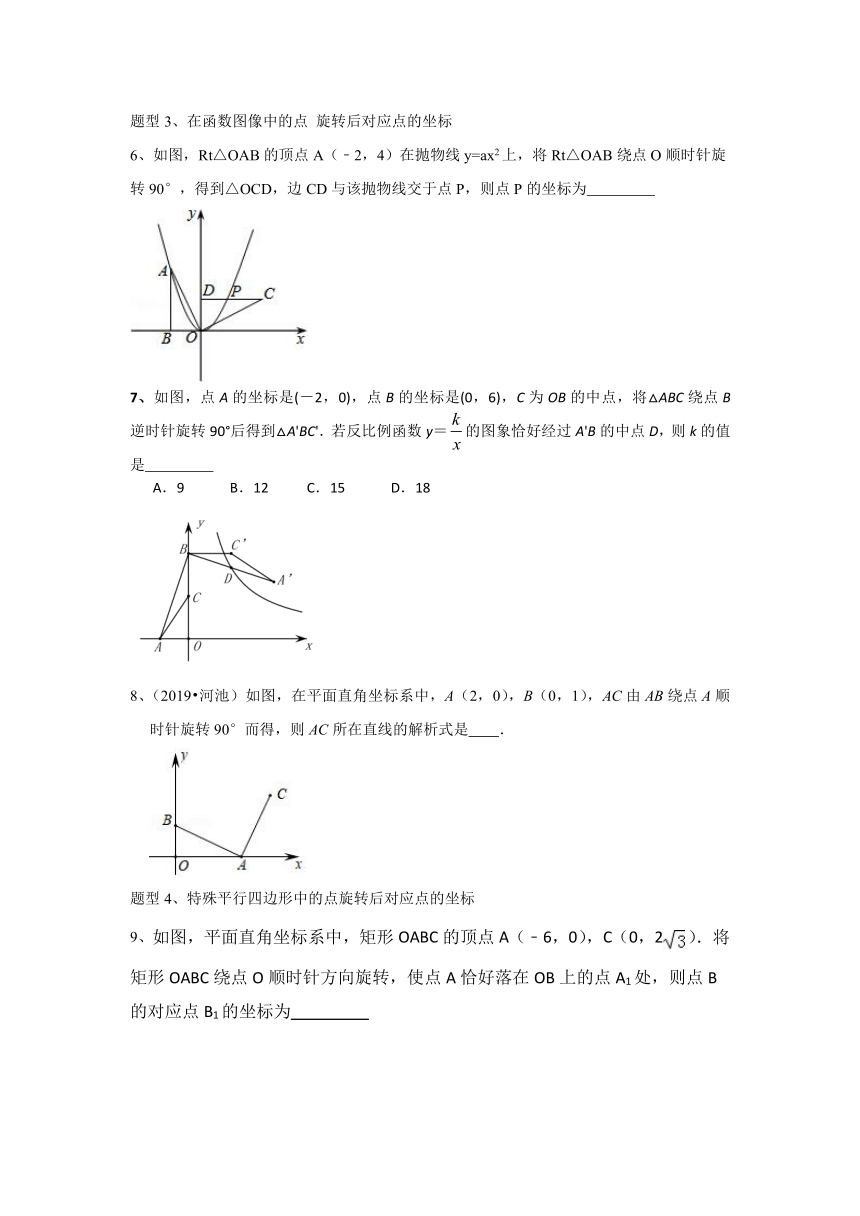
6、如图,Rt△OAB的顶点 A(﹣2,4)在抛物线 y=ax2上,将 Rt△OAB绕点 O顺时针旋
转 90°,得到△OCD,边 CD与该抛物线交于点 P,则点 P的坐标为
7、如图,点 A 的坐标是(-2,0),点 B 的坐标是(0,6),C 为 OB 的中点,将△ABC 绕点 B
逆时针旋转 90°后得到△A'BC'.若反比例函数 y=
k
x
的图象恰好经过 A'B 的中点 D,则 k的值
是
A.9 B.12 C.15 D.18
8、(2019?河池)如图,在平面直角坐标系中,A(2,0),B(0,1),AC由 AB绕点 A顺
时针旋转 90°而得,则 AC所在直线的解析式是 .
题型 4、特殊平行四边形中的点旋转后对应点的坐标
9、如图,平面直角坐标系中,矩形 OABC 的顶点 A(﹣6,0),C(0,2 ).将
矩形 OABC 绕点 O 顺时针方向旋转,使点 A 恰好落在 OB 上的点 A1处,则点 B
的对应点 B1的坐标为
10、如图,在平面直角坐标系 xOy 中,菱形 OABC 的边长为 2,点 A 在第一象限,
点 C 在 x 轴正半轴上,∠AOC=60°,若将菱形 OABC 绕点 O 顺时针旋转 75°,得
到四边形 OA′B′C′,则点 B 的对应点 B′的坐标为 .
11、如图,已知菱形 OABC 的顶点 O(0,0),B(2,2),若菱形绕点 O 逆时
针旋转,每秒旋转 45°,则第 60秒时,菱形的对角线交点 D 的坐标为
A.(1,﹣1) B.(﹣1,﹣1) C.( ,0) D.(0,﹣ )
12、(2019?河南)如图,在△OAB中,顶点 O(0,0),A(﹣3,4),B(3,4),将△OAB
与正方形 ABCD组成的图形绕点 O顺时针旋转,每次旋转 90°,则第 70次旋转结束时,
点 D的坐标为
A.(10,3) B.(﹣3,10) C.(10,﹣3) D.(3,﹣10)
中考在线:
1、(2019?荆州)在平面直角坐标系中,点 A的坐标为(1, ),以原点为中心,将点 A
顺时针旋转 30°得到点 A',则点 A'的坐标为
A.( ,1) B.( ,﹣1) C.(2,1) D.(0,2)
2、(2019?枣庄)如图,点 E是正方形 ABCD的边 DC上一点,把△ADE绕点 A顺时针旋转
90°到△ABF的位置.若四边形 AECF的面积为 20,DE=2,则 AE的长为
A.4 B.2 C.6 D.2
3、(2019?湘潭)如图,将△OAB绕点 O逆时针旋转 70°到△OCD的位置,若∠AOB=40°,
则∠AOD=
A.45° B.40° C.35° D.30°
4、(2019?内江)如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点 A顺时
针旋转得到△ADE,当点 B的对应点 D恰好落在 BC边上时,则 CD的长为
A.1.6 B.1.8 C.2 D.2.6
5、(2019?荆门)如图,Rt△OCB的斜边在 y轴上,OC= ,含 30°角的顶点与原点重合,
直角顶点 C在第二象限,将 Rt△OCB绕原点顺时针旋转 120°后得到△OC′B',则 B点
的对应点 B′的坐标是
A.( ,﹣1) B.(1,﹣ ) C.(2,0) D.( ,0)
6、(2019?阜新)如图,在△ABC中,AC=BC,将△ABC绕点 A逆时针旋转 60°,得到△
ADE.若 AB=2,∠ACB=30°,则线段 CD的长度为 .
7、(2019?包头)如图,在△ABC中,∠CAB=55°,∠ABC=25°,在同一平面内,将△
ABC绕 A点逆时针旋转 70°得到△ADE,连接 EC,则 tan∠DEC的值是 .
8、(2019?青海)如图,在直角坐标系中,已知点 A(3,2),将△ABO绕点 O逆时针方向
旋转 180°后得到△CDO,则点 C的坐标是 .
9、(2019?镇江)将边长为 1的正方形 ABCD绕点 C按顺时针方向旋转到 FECG的位置(如
图),使得点 D落在对角线 CF上,EF与 AD相交于点 H,则 HD= .(结果保留根
号)
10、如图,正方形 ABCD 绕点 B 逆时针旋转 30°后得到正方形 BEFG,EF 与 AD 相交于点 H,
延长 DA 交 GF 于点 K.若正方形 ABCD 边长为 3,则 AK= .
11、如图,在边长为 1的正方形组成的网格中,△AOB 的顶点均在格点上,其中点 A(5,4),
B(1,3),将△AOB 绕点 O 逆时针旋转 90°后得到△A1OB1.
(1)画出△A1OB1;
(2)在旋转过程中点 B 所经过的路径长为 ;
(3)求在旋转过程中线段 AB、BO 扫过的图形的面积之和.
参考答案:
(一)三角形的旋转
题型 1、求角的度数 1、A. 2、22.5°
题型 2、求线段的长度 3、2 ﹣2 4、
题型 3、求旋转重合的图形面积 5、6 3 .
题型 4、特殊三角形的旋转 6、 62 ? 7、 2
3
(二)特殊平行四边形旋转 1、B 2、D 3、 ﹣1
(三)平面直角坐标系中的旋转
题型 1、求旋转后对应点的坐标 1、D 2、B 3、B
题型 2、求三角形旋转后对应点的坐标 4、C 5、(1+ 2 ,0)
题型 3、在函数图像中的点 旋转后对应点的坐标 6、( ,2) 7、C 8、y=2x﹣4
题型 4、特殊平行四边形中的点旋转后对应点的坐标
9、(﹣2 ,6) 10、( ,﹣ ) 11、B 12、D
中考在线:1、A 2、D 3、D 4、A 5、A
6、2 7、1 8、(﹣3,﹣2) 9、 ﹣1 10、 3-32 11、π
在解决旋转问题时,应注意旋转前后相对应的边相等、角相,旋转角度在计
算过程中的应用等。下面着重从三个方面进行讲述:三角形旋转、特殊平行四边
形旋转和在平面直角坐标系内的图形旋转三大类进行。
(一)三角形的旋转
题型 1、求角的度数
1、如图,在△ABC 中,∠CAB=75°,将△ABC 在平面内绕点 A 旋转到△AB′C′的位
置,使 CC′∥AB,则旋转角的度数为
A.30° B.40° C.50° D.75°
2、(2019?常德)如图,已知△ABC是等腰三角形,AB=AC,∠BAC=45°,点 D在 AC
边上,将△ABD绕点 A逆时针旋转 45°得到△ACD′,且点 D′、D、B三点在同一条直
线上,则∠ABD的度数是 .
题型 2、求线段的长度
3、(2019?新疆)如图,在△ABC中,AB=AC=4,将△ABC绕点 A顺时针旋转 30°,得
到△ACD,延长 AD交 BC的延长线于点 E,则 DE的长为 .
4、(2019?哈尔滨)如图,将△ABC绕点 C逆时针旋转得到△A′B′C,其中点 A′与 A是
对应点,点 B′与 B是对应点,点 B′落在边 AC上,连接 A′B,若∠ACB=45°,AC
=3,BC=2,则 A′B的长为 .
题型 3、求旋转重合的图形面积
5、如图,等腰直角三角形 ABC 的直角边 AB 的长为 6cm,将△ABC 绕点 A 逆时针旋转 15°后
得到△AB′C′,则图中阴影部分面积等于 cm
2
.
题型 4、特殊三角形的旋转
6、(2019 绵阳)如图,△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,
DE=2 �.将△BDE绕点 B逆时针方向旋转后得△BD′E′,当点 E′恰好落在线段 AD′上时,则
CE′=______.
7、(2019 眉山)如图,在 Rt△ABC中,∠B=900,AB=5,BC=12,将△ABC绕点 A逆时
针旋转得到△ADE,使得点 D落在 AC上,则 tan∠ECD的值为 .
B
A D C
E
(二)特殊平行四边形旋转
1、如图,将矩形 ABCD 绕点 A 旋转至矩形 AB′C′D′位置,此时 AC 的中点恰好与 D 点重合,
AB 交 CD 于点 E.若 AB=6,则△AEC 的面积为
A.12 B.4 3 C.8 3 D.6
2、如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到
的位置,若四边形 的面积为 25, ,则 的长为
A. 5 B. C. 7 D.
3、如图,在菱形 ABCD中,AB=2,∠BAD=60°,将菱形 ABCD绕点 A逆时针方向旋转,
对应得到菱形 AEFG,点 E在 AC上,EF与 CD交于点 P,则 DP的长是 .
(三)平面直角坐标系中的旋转
题型 1、求点旋转后对应点的坐标
1、在平面直角坐标系中,将△AOB绕原点 O顺时针旋转 180°后得到△A1OB1,若点 B
的坐标为(2,1),则点 B的对应点 B1 的坐标为
A.(1,2) B.(2,﹣1) C.(﹣2,1) D.(﹣2,﹣1)
2、如图,将线段 AB绕点 O顺时针旋转 90°得到线段 A′B′,那么 A(﹣2,5)的对应
点 A′的坐标是
A.(2,5) B.(5,2) C.(2,﹣5) D.(5,﹣2)
3、如图所示,在平面直角坐标系中,点 A、B的坐标分别为(-2,0)和(2,0).月牙①
绕点 B顺时针旋转 90°得到月牙②,则点 A的对应点 A′的坐标为
A.(2,2) B.(2,4) C.(4,2) D.(1,2)
题型 2、求三角形旋转后对应点的坐标
4、将含有 30°角的直角三角板 OAB如图放置在平面直角坐标系中,OB在 x轴上,若 OA=2,
将三角板绕原点 O顺时针旋转 75°,则点 A的对应点 A′的坐标为
A.( ,﹣1) B.(1,﹣ ) C.( ,﹣ ) D.(﹣ , )
5、将一个含 45°角的三角板 ABC如图摆放在平面直角坐标系中,将其绕点 C顺时针旋转
75°,点B的对应点B′恰好落在 x轴上,若点C的坐标为(1,0),则点B′的坐标为 .
题型 3、在函数图像中的点 旋转后对应点的坐标
6、如图,Rt△OAB的顶点 A(﹣2,4)在抛物线 y=ax2上,将 Rt△OAB绕点 O顺时针旋
转 90°,得到△OCD,边 CD与该抛物线交于点 P,则点 P的坐标为
7、如图,点 A 的坐标是(-2,0),点 B 的坐标是(0,6),C 为 OB 的中点,将△ABC 绕点 B
逆时针旋转 90°后得到△A'BC'.若反比例函数 y=
k
x
的图象恰好经过 A'B 的中点 D,则 k的值
是
A.9 B.12 C.15 D.18
8、(2019?河池)如图,在平面直角坐标系中,A(2,0),B(0,1),AC由 AB绕点 A顺
时针旋转 90°而得,则 AC所在直线的解析式是 .
题型 4、特殊平行四边形中的点旋转后对应点的坐标
9、如图,平面直角坐标系中,矩形 OABC 的顶点 A(﹣6,0),C(0,2 ).将
矩形 OABC 绕点 O 顺时针方向旋转,使点 A 恰好落在 OB 上的点 A1处,则点 B
的对应点 B1的坐标为
10、如图,在平面直角坐标系 xOy 中,菱形 OABC 的边长为 2,点 A 在第一象限,
点 C 在 x 轴正半轴上,∠AOC=60°,若将菱形 OABC 绕点 O 顺时针旋转 75°,得
到四边形 OA′B′C′,则点 B 的对应点 B′的坐标为 .
11、如图,已知菱形 OABC 的顶点 O(0,0),B(2,2),若菱形绕点 O 逆时
针旋转,每秒旋转 45°,则第 60秒时,菱形的对角线交点 D 的坐标为
A.(1,﹣1) B.(﹣1,﹣1) C.( ,0) D.(0,﹣ )
12、(2019?河南)如图,在△OAB中,顶点 O(0,0),A(﹣3,4),B(3,4),将△OAB
与正方形 ABCD组成的图形绕点 O顺时针旋转,每次旋转 90°,则第 70次旋转结束时,
点 D的坐标为
A.(10,3) B.(﹣3,10) C.(10,﹣3) D.(3,﹣10)
中考在线:
1、(2019?荆州)在平面直角坐标系中,点 A的坐标为(1, ),以原点为中心,将点 A
顺时针旋转 30°得到点 A',则点 A'的坐标为
A.( ,1) B.( ,﹣1) C.(2,1) D.(0,2)
2、(2019?枣庄)如图,点 E是正方形 ABCD的边 DC上一点,把△ADE绕点 A顺时针旋转
90°到△ABF的位置.若四边形 AECF的面积为 20,DE=2,则 AE的长为
A.4 B.2 C.6 D.2
3、(2019?湘潭)如图,将△OAB绕点 O逆时针旋转 70°到△OCD的位置,若∠AOB=40°,
则∠AOD=
A.45° B.40° C.35° D.30°
4、(2019?内江)如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点 A顺时
针旋转得到△ADE,当点 B的对应点 D恰好落在 BC边上时,则 CD的长为
A.1.6 B.1.8 C.2 D.2.6
5、(2019?荆门)如图,Rt△OCB的斜边在 y轴上,OC= ,含 30°角的顶点与原点重合,
直角顶点 C在第二象限,将 Rt△OCB绕原点顺时针旋转 120°后得到△OC′B',则 B点
的对应点 B′的坐标是
A.( ,﹣1) B.(1,﹣ ) C.(2,0) D.( ,0)
6、(2019?阜新)如图,在△ABC中,AC=BC,将△ABC绕点 A逆时针旋转 60°,得到△
ADE.若 AB=2,∠ACB=30°,则线段 CD的长度为 .
7、(2019?包头)如图,在△ABC中,∠CAB=55°,∠ABC=25°,在同一平面内,将△
ABC绕 A点逆时针旋转 70°得到△ADE,连接 EC,则 tan∠DEC的值是 .
8、(2019?青海)如图,在直角坐标系中,已知点 A(3,2),将△ABO绕点 O逆时针方向
旋转 180°后得到△CDO,则点 C的坐标是 .
9、(2019?镇江)将边长为 1的正方形 ABCD绕点 C按顺时针方向旋转到 FECG的位置(如
图),使得点 D落在对角线 CF上,EF与 AD相交于点 H,则 HD= .(结果保留根
号)
10、如图,正方形 ABCD 绕点 B 逆时针旋转 30°后得到正方形 BEFG,EF 与 AD 相交于点 H,
延长 DA 交 GF 于点 K.若正方形 ABCD 边长为 3,则 AK= .
11、如图,在边长为 1的正方形组成的网格中,△AOB 的顶点均在格点上,其中点 A(5,4),
B(1,3),将△AOB 绕点 O 逆时针旋转 90°后得到△A1OB1.
(1)画出△A1OB1;
(2)在旋转过程中点 B 所经过的路径长为 ;
(3)求在旋转过程中线段 AB、BO 扫过的图形的面积之和.
参考答案:
(一)三角形的旋转
题型 1、求角的度数 1、A. 2、22.5°
题型 2、求线段的长度 3、2 ﹣2 4、
题型 3、求旋转重合的图形面积 5、6 3 .
题型 4、特殊三角形的旋转 6、 62 ? 7、 2
3
(二)特殊平行四边形旋转 1、B 2、D 3、 ﹣1
(三)平面直角坐标系中的旋转
题型 1、求旋转后对应点的坐标 1、D 2、B 3、B
题型 2、求三角形旋转后对应点的坐标 4、C 5、(1+ 2 ,0)
题型 3、在函数图像中的点 旋转后对应点的坐标 6、( ,2) 7、C 8、y=2x﹣4
题型 4、特殊平行四边形中的点旋转后对应点的坐标
9、(﹣2 ,6) 10、( ,﹣ ) 11、B 12、D
中考在线:1、A 2、D 3、D 4、A 5、A
6、2 7、1 8、(﹣3,﹣2) 9、 ﹣1 10、 3-32 11、π
同课章节目录
