中考数学专题复习图形变换——平移、对称、位似问题(PDF版,附答案)
文档属性
| 名称 | 中考数学专题复习图形变换——平移、对称、位似问题(PDF版,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 242.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 00:00:00 | ||
图片预览

文档简介
二轮复习:图形变换(三)—平移、对称、位似
一、平移:
题型 1、点的平移:口诀:上加下减、左减右加
1、在平面直角坐标系中,将点 A(1,﹣2)向上平移 3个单位长度,再向左平移 2个单位
长度,得到点 B,则点 B的坐标是
A.(﹣1,1) B.(3,1) C.(4,﹣4) D.(4,0)
题型 2、函数图像上点的平移:口诀:上加下减、左加右减
2、在平面直角坐标系中,将直线 L1:y=-2x-2 平移后,得到直线 L2:y=-2x+4,则下列平移
正确的是
A、.将 L1向右平移 3个单位长度 B.、将 L1向右平移 6个单位长度
C.、将 L1向上平移 2个单位长度 D、.将 L1向上平移 4个单位长度
3、如图,直线 y=2x+4 与 x,y 轴分别交于 A,B 两点,以 OB 为边在 y 轴右侧作等边△OBC,
将点 C 向左平移,使其对应点 C′恰好落在直线 AB 上,则点 C′的坐标为 .
4、反比例函数
x
ky ? 的图象上有一点 P(2,n),将点 P 向右平移 1 个单位,再向下平移 1 个
单位得到点 Q.若点 Q 也在该函数的图象上,则 k= .
5、将抛物线 y=﹣5x2+1 向左平移 1个单位长度,再向下平移 2个单位长度,所得
到的抛物线为
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
6、将抛物线 y= x2﹣6x+21 向左平移 2个单位后,得到新抛物线的解析式为
A.y= (x﹣8)2+5 B.y= (x﹣4)2+5
C.y= (x﹣8)2+3 D.y= (x﹣4)2+3
题型 3、图形的平移:做法:找图形上的点进行平移,得到整个图形的平移
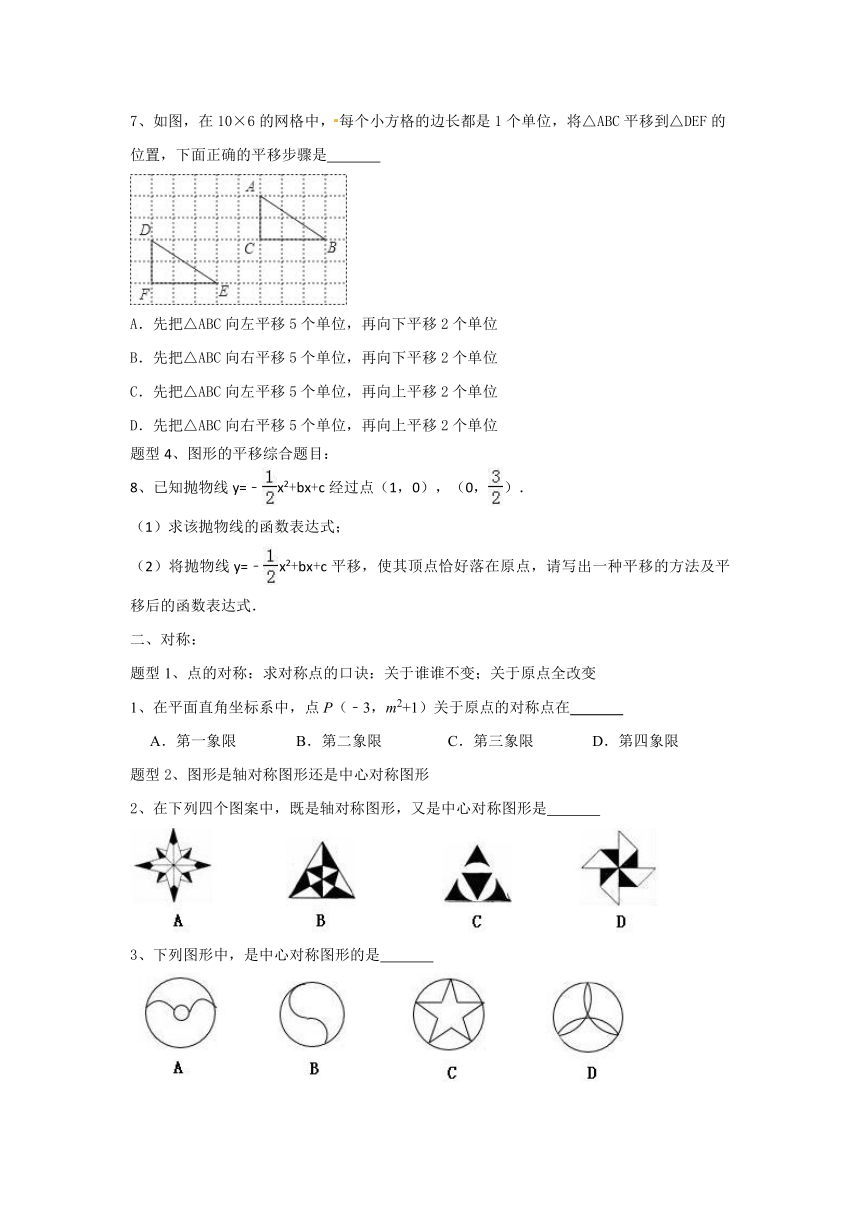
7、如图,在 10×6 的网格中, 每个小方格的边长都是 1 个单位,将△ABC 平移到△DEF 的
位置,下面正确的平移步骤是
A.先把△ABC 向左平移 5个单位,再向下平移 2个单位
B.先把△ABC 向右平移 5个单位,再向下平移 2个单位
C.先把△ABC 向左平移 5个单位,再向上平移 2个单位
D.先把△ABC 向右平移 5个单位,再向上平移 2个单位
题型 4、图形的平移综合题目:
8、已知抛物线 y=﹣ x2+bx+c 经过点(1,0),(0, ).
(1)求该抛物线的函数表达式;
(2)将抛物线 y=﹣ x2+bx+c 平移,使其顶点恰好落在原点,请写出一种平移的方法及平
移后的函数表达式.
二、对称:
题型 1、点的对称:求对称点的口诀:关于谁谁不变;关于原点全改变
1、在平面直角坐标系中,点 P(﹣3,m2+1)关于原点的对称点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
题型 2、图形是轴对称图形还是中心对称图形
2、在下列四个图案中,既是轴对称图形,又是中心对称图形是
3、下列图形中,是中心对称图形的是
三、位似
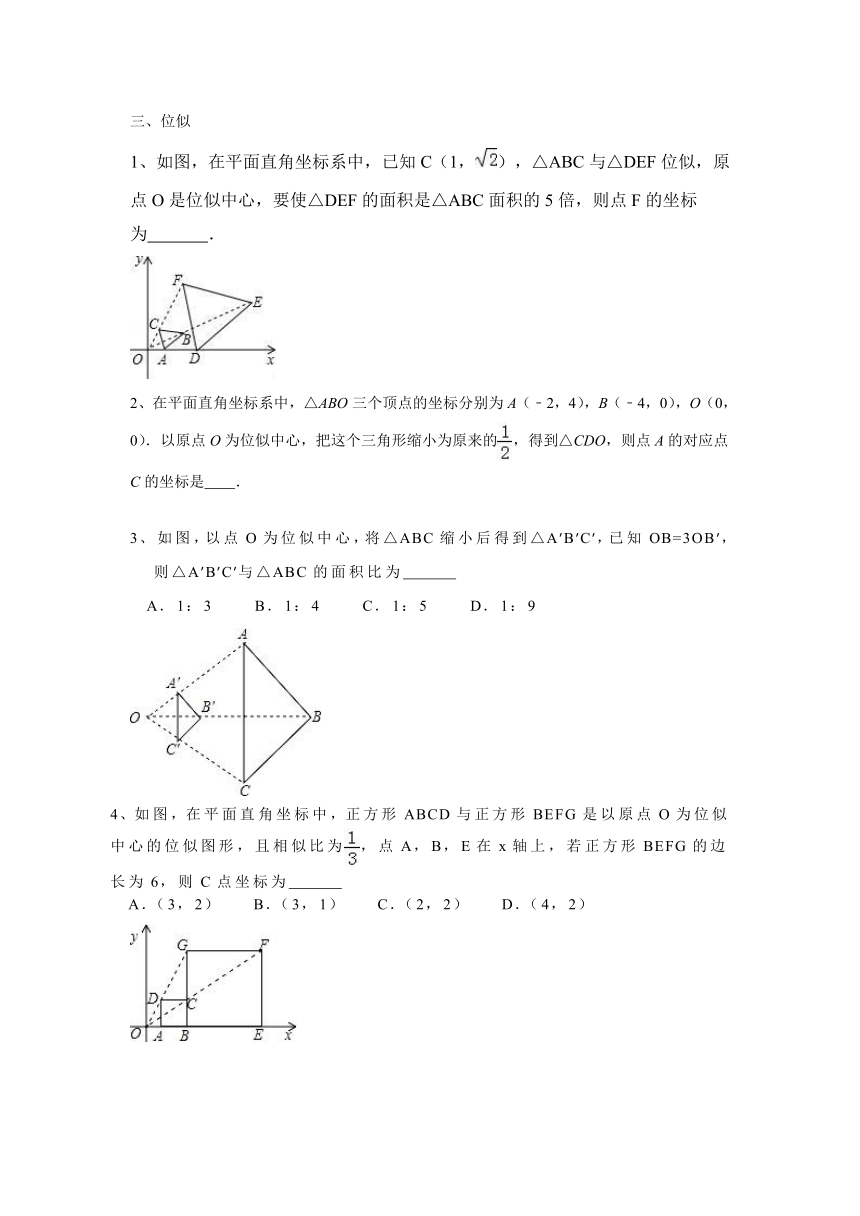
1、如图,在平面直角坐标系中,已知 C(1, ),△ABC与△DEF位似,原
点 O是位似中心,要使△DEF的面积是△ABC面积的 5倍,则点 F的坐标
为 .
2、在平面直角坐标系中,△ABO三个顶点的坐标分别为 A(﹣2,4),B(﹣4,0),O(0,
0).以原点 O为位似中心,把这个三角形缩小为原来的 ,得到△CDO,则点 A的对应点
C的坐标是 .
3、如图,以点 O 为位似中心,将△ABC 缩小后得到△A ′B ′C ′,已知 OB=3OB ′,
则△A ′B ′C ′与△ABC 的面积比为
A. 1: 3 B. 1: 4 C. 1: 5 D. 1: 9
4、如图,在平面直角坐标中,正方形 ABCD 与正方形 BEFG 是以原点 O 为位似
中心的位似图形,且相似比为 ,点 A,B, E 在 x 轴上,若正方形 BEFG 的边
长为 6,则 C 点坐标为
A.( 3, 2) B.( 3, 1) C.( 2, 2) D.( 4, 2)
中考在线:
1、若点 A 的坐标是(-2,3),点 B 与点 A 关于原点对称,点 C 与点 B 关于 y轴对称,则点
C 的坐标是____
2、△A’B’C’是由△ABC 平移得到的,点 A(-1,-4)的对应点为 A’(1,-1),则
点 B(1,1)的对应点 B’、点 C(-1,4)的对应点 C’的坐标分别为
A、(2,2)(3,4) B、(3,4)(1,7)
C、(-2,2)(1,7) D、(3,4)(2,-2)
3、抛物线 y=(x﹣2)2﹣1 可以由抛物线 y=x2平移而得到,下列平移正确的是
A.先向左平移 2 个单位长度,然后向上平移 1 个单位长度
B.先向左平移 2 个单位长度,然后向下平移 1 个单位长度
C.先向右平移 2 个单位长度,然后向上平移 1 个单位长度
D.先向右平移 2 个单位长度,然后向下平移 1 个单位长度
4、若抛物线 y=x2+ax+b 与 x 轴两个交点间的距离为 2,称此抛物线为定弦抛物线,已知某
定弦抛物线的对称轴为直线 x=1,将此抛物线向左平移 2 个单位,再向下平移 3 个单位,得
到的抛物线过点
A.(﹣3,﹣6) B.(﹣3,0) C.(﹣3,﹣5) D.(﹣3,﹣1)
5、如图,点 P(8,6)在△ABC的边 AC上,以原点 O为位似中心,在第一象限内将△ABC
缩小到原来的 ,得到△A′B′C′,点 P在 A′C′上的对应点 P′的坐标为
A.(4,3) B.(3,4) C.(5,3) D.(4,4)
6、如图,在直角坐标系中,已知菱形 OABC的顶点 A(1,2),B(3,3).作菱形 OABC
关于 y轴的对称图形 OA'B'C',再作图形 OA'B'C'关于点 O的中心对称图形 OA″B″C″,则
点 C的对应点 C″的坐标是
A.(2,﹣1) B.(1,﹣2) C.(﹣2,1) D.(﹣2,﹣1)
7、在平面直角坐标系中,点 A,B的坐标分别是 A(4,2),B(5,0),以点 O为位似中心,
相似比为 ,把△ABO缩小,得到△A1B1O,则点 A的对应点 A1的坐标为 .
8、已知二次函数的图象以 A(﹣1,4)为顶点,且过点 B(2,﹣5)
①求该函数的关系式;
②求该函数图象与坐标轴的交点坐标;
③将该函数图象向右平移,当图象经过原点时,A、B 两点随图象移至 A′、B′,
求△O A′B′的面积.
参考答案:
一、平移:
题型 1、点的平移:1、A
题型 2、函数图像上点的平移: 2、A 3(﹣1,2) 4、6 5、A 6、D
题型 3、图形的平移:7、A
题型 4、图形的平移综合题目:8、解:(1)把(1,0),(0, )代入抛物线解
析式得: ,解得: ,
则抛物线解析式为 y=﹣ x2﹣x+ ;
(2)抛物线解析式为 y=﹣ x2﹣x+ =﹣ (x+1)2+2,
将抛物线向右平移一个单位,向下平移 2个单位,解析式变为 y=﹣ x2.
二、 对称:题型 1、点的对称:1、D 2、A 3、B
三、位似
1、( , ) 2、(﹣1,2)或(1,﹣2) 3、D 4、A
中考在线:1、(-2、-3) 2、B 3、D 4、B 5、A 6、A
7、(2,1)或(﹣2,﹣1)
8、解:(1)设抛物线顶点式 y=a(x+1)2+4
将 B(2,﹣5)代入得:a=﹣1
∴该函数的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3
(2)令 x=0,得 y=3,因此抛物线与 y 轴的交点为:(0,3)
令 y=0,﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,即抛物线与 x 轴的交点为:(﹣3,
0),(1,0)
(3)设抛物线与 x轴的交点为 M、N(M在 N 的左侧),由(2)知:M(﹣3,
0),N(1,0)
当函数图象向右平移经过原点时,M与 O 重合,
因此抛物线向右平移了 3个单位故 A'(2,4),B'(5,﹣5)
∴S△OA′B′= ×(2+5)×9﹣ ×2×4﹣ ×5×5=15.
一、平移:
题型 1、点的平移:口诀:上加下减、左减右加
1、在平面直角坐标系中,将点 A(1,﹣2)向上平移 3个单位长度,再向左平移 2个单位
长度,得到点 B,则点 B的坐标是
A.(﹣1,1) B.(3,1) C.(4,﹣4) D.(4,0)
题型 2、函数图像上点的平移:口诀:上加下减、左加右减
2、在平面直角坐标系中,将直线 L1:y=-2x-2 平移后,得到直线 L2:y=-2x+4,则下列平移
正确的是
A、.将 L1向右平移 3个单位长度 B.、将 L1向右平移 6个单位长度
C.、将 L1向上平移 2个单位长度 D、.将 L1向上平移 4个单位长度
3、如图,直线 y=2x+4 与 x,y 轴分别交于 A,B 两点,以 OB 为边在 y 轴右侧作等边△OBC,
将点 C 向左平移,使其对应点 C′恰好落在直线 AB 上,则点 C′的坐标为 .
4、反比例函数
x
ky ? 的图象上有一点 P(2,n),将点 P 向右平移 1 个单位,再向下平移 1 个
单位得到点 Q.若点 Q 也在该函数的图象上,则 k= .
5、将抛物线 y=﹣5x2+1 向左平移 1个单位长度,再向下平移 2个单位长度,所得
到的抛物线为
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
6、将抛物线 y= x2﹣6x+21 向左平移 2个单位后,得到新抛物线的解析式为
A.y= (x﹣8)2+5 B.y= (x﹣4)2+5
C.y= (x﹣8)2+3 D.y= (x﹣4)2+3
题型 3、图形的平移:做法:找图形上的点进行平移,得到整个图形的平移
7、如图,在 10×6 的网格中, 每个小方格的边长都是 1 个单位,将△ABC 平移到△DEF 的
位置,下面正确的平移步骤是
A.先把△ABC 向左平移 5个单位,再向下平移 2个单位
B.先把△ABC 向右平移 5个单位,再向下平移 2个单位
C.先把△ABC 向左平移 5个单位,再向上平移 2个单位
D.先把△ABC 向右平移 5个单位,再向上平移 2个单位
题型 4、图形的平移综合题目:
8、已知抛物线 y=﹣ x2+bx+c 经过点(1,0),(0, ).
(1)求该抛物线的函数表达式;
(2)将抛物线 y=﹣ x2+bx+c 平移,使其顶点恰好落在原点,请写出一种平移的方法及平
移后的函数表达式.
二、对称:
题型 1、点的对称:求对称点的口诀:关于谁谁不变;关于原点全改变
1、在平面直角坐标系中,点 P(﹣3,m2+1)关于原点的对称点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
题型 2、图形是轴对称图形还是中心对称图形
2、在下列四个图案中,既是轴对称图形,又是中心对称图形是
3、下列图形中,是中心对称图形的是
三、位似
1、如图,在平面直角坐标系中,已知 C(1, ),△ABC与△DEF位似,原
点 O是位似中心,要使△DEF的面积是△ABC面积的 5倍,则点 F的坐标
为 .
2、在平面直角坐标系中,△ABO三个顶点的坐标分别为 A(﹣2,4),B(﹣4,0),O(0,
0).以原点 O为位似中心,把这个三角形缩小为原来的 ,得到△CDO,则点 A的对应点
C的坐标是 .
3、如图,以点 O 为位似中心,将△ABC 缩小后得到△A ′B ′C ′,已知 OB=3OB ′,
则△A ′B ′C ′与△ABC 的面积比为
A. 1: 3 B. 1: 4 C. 1: 5 D. 1: 9
4、如图,在平面直角坐标中,正方形 ABCD 与正方形 BEFG 是以原点 O 为位似
中心的位似图形,且相似比为 ,点 A,B, E 在 x 轴上,若正方形 BEFG 的边
长为 6,则 C 点坐标为
A.( 3, 2) B.( 3, 1) C.( 2, 2) D.( 4, 2)
中考在线:
1、若点 A 的坐标是(-2,3),点 B 与点 A 关于原点对称,点 C 与点 B 关于 y轴对称,则点
C 的坐标是____
2、△A’B’C’是由△ABC 平移得到的,点 A(-1,-4)的对应点为 A’(1,-1),则
点 B(1,1)的对应点 B’、点 C(-1,4)的对应点 C’的坐标分别为
A、(2,2)(3,4) B、(3,4)(1,7)
C、(-2,2)(1,7) D、(3,4)(2,-2)
3、抛物线 y=(x﹣2)2﹣1 可以由抛物线 y=x2平移而得到,下列平移正确的是
A.先向左平移 2 个单位长度,然后向上平移 1 个单位长度
B.先向左平移 2 个单位长度,然后向下平移 1 个单位长度
C.先向右平移 2 个单位长度,然后向上平移 1 个单位长度
D.先向右平移 2 个单位长度,然后向下平移 1 个单位长度
4、若抛物线 y=x2+ax+b 与 x 轴两个交点间的距离为 2,称此抛物线为定弦抛物线,已知某
定弦抛物线的对称轴为直线 x=1,将此抛物线向左平移 2 个单位,再向下平移 3 个单位,得
到的抛物线过点
A.(﹣3,﹣6) B.(﹣3,0) C.(﹣3,﹣5) D.(﹣3,﹣1)
5、如图,点 P(8,6)在△ABC的边 AC上,以原点 O为位似中心,在第一象限内将△ABC
缩小到原来的 ,得到△A′B′C′,点 P在 A′C′上的对应点 P′的坐标为
A.(4,3) B.(3,4) C.(5,3) D.(4,4)
6、如图,在直角坐标系中,已知菱形 OABC的顶点 A(1,2),B(3,3).作菱形 OABC
关于 y轴的对称图形 OA'B'C',再作图形 OA'B'C'关于点 O的中心对称图形 OA″B″C″,则
点 C的对应点 C″的坐标是
A.(2,﹣1) B.(1,﹣2) C.(﹣2,1) D.(﹣2,﹣1)
7、在平面直角坐标系中,点 A,B的坐标分别是 A(4,2),B(5,0),以点 O为位似中心,
相似比为 ,把△ABO缩小,得到△A1B1O,则点 A的对应点 A1的坐标为 .
8、已知二次函数的图象以 A(﹣1,4)为顶点,且过点 B(2,﹣5)
①求该函数的关系式;
②求该函数图象与坐标轴的交点坐标;
③将该函数图象向右平移,当图象经过原点时,A、B 两点随图象移至 A′、B′,
求△O A′B′的面积.
参考答案:
一、平移:
题型 1、点的平移:1、A
题型 2、函数图像上点的平移: 2、A 3(﹣1,2) 4、6 5、A 6、D
题型 3、图形的平移:7、A
题型 4、图形的平移综合题目:8、解:(1)把(1,0),(0, )代入抛物线解
析式得: ,解得: ,
则抛物线解析式为 y=﹣ x2﹣x+ ;
(2)抛物线解析式为 y=﹣ x2﹣x+ =﹣ (x+1)2+2,
将抛物线向右平移一个单位,向下平移 2个单位,解析式变为 y=﹣ x2.
二、 对称:题型 1、点的对称:1、D 2、A 3、B
三、位似
1、( , ) 2、(﹣1,2)或(1,﹣2) 3、D 4、A
中考在线:1、(-2、-3) 2、B 3、D 4、B 5、A 6、A
7、(2,1)或(﹣2,﹣1)
8、解:(1)设抛物线顶点式 y=a(x+1)2+4
将 B(2,﹣5)代入得:a=﹣1
∴该函数的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3
(2)令 x=0,得 y=3,因此抛物线与 y 轴的交点为:(0,3)
令 y=0,﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,即抛物线与 x 轴的交点为:(﹣3,
0),(1,0)
(3)设抛物线与 x轴的交点为 M、N(M在 N 的左侧),由(2)知:M(﹣3,
0),N(1,0)
当函数图象向右平移经过原点时,M与 O 重合,
因此抛物线向右平移了 3个单位故 A'(2,4),B'(5,﹣5)
∴S△OA′B′= ×(2+5)×9﹣ ×2×4﹣ ×5×5=15.
同课章节目录
