北师大版数学七年级下册5.3简单的轴对称图形课件(第一课时,共24张PPT)
文档属性
| 名称 | 北师大版数学七年级下册5.3简单的轴对称图形课件(第一课时,共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 16:00:43 | ||
图片预览







文档简介
(共24张PPT)
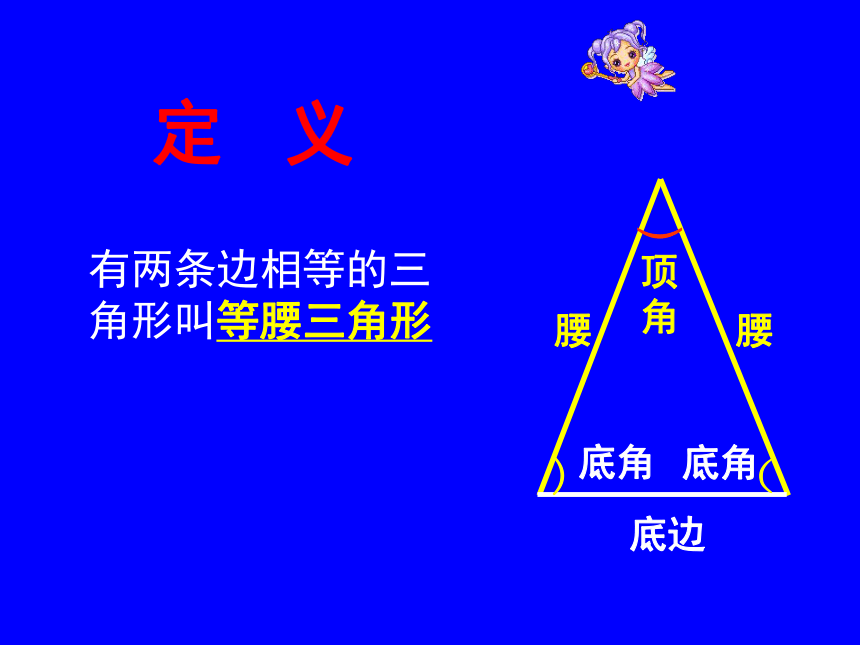
有两条边相等的三角形叫等腰三角形
定 义
等腰三角形是轴对称图形吗?
拿出等腰三角形纸片,折折看,你能发现什么现象?
实践出真知
动手做一做
看我七十二变
聪明的你看明白了吗?
(1)等腰三角形是轴对称图形
(2)∠B=∠C
(3)∠BAD=∠CAD,AD为顶角的平分线
(4)∠ADB=∠ADC=90°,AD为底边上的高
(5)BD=CD,AD为底边上的中线。
现象:
在等腰ΔABC中,已知AB=AC,作顶角平分线
AD,则∠BAD=∠CAD.
言之有理
在ΔABD和ΔACD中,
∵AB=AC,∠BAD=∠CAD,AD=AD
∴ΔABD≌ΔACD(SAS)
∴BD=CD,∠ADB=∠ADC=90?,∠B=∠C
(全等三角形对应边相等,对应角相等)
∴AD是等腰ΔABC的顶角平分线、底边上的中
线、底边上的高;等腰ΔABC的两个底角相等。
1.等腰三角形是轴对称图形。
3.等腰三角形的两个底角相等(也称“等边对等角”)。
2.等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
有两个角相等的三角形是等腰三角形吗?
在ΔABC中,已知∠B=∠C,作顶角的
平分线AD,则∠BAD=∠CAD .
言之有理
在ΔABD和ΔACD中,
∵∠B=∠C,∠BAD=∠CAD,AD=AD
∴ΔABD≌ΔACD(AAS)
∴AB=AC(全等三角形对应边相等)
∴ΔABC是等腰三角形。
1.有两条边相等的三角形是等腰三角形(定义法)。
2.有两个角相等的三角形是等腰三角形(也称“等角对等边”)。
等边三角形是特殊的等腰三角
形,它的三边都相等。
你能发现它的哪些特征?
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形每个角的平分线和这个角的对 边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
3.等边三角形的各内角都相等,都等于60°。
1、如图,是由大小不等的等边三角形组成的图案,请找出它的对称轴。
2、墙上钉了一根木条,小明想检验这根木条是否水平。他拿来一个如图所示的测平仪,在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤。小明将BC边与木条重合,观察此时悬挂重锤的细线是否通过A点就能做出判断。你能说明其中的道理吗?
答:据题意,AD是等腰三角形ABC的中线,根据等腰三角形“三线合一”的性质,AD也是底边BC上的高,即AD⊥BC,如果悬挂重锤的细线通过A点,则说明木条所在直线垂直于铅垂线,即木条水平。
3、如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使A、B到它的距离之和最短。
C
E
D
.
.
4、一个等腰三角形的底角是顶角的2倍,求它的各个内角的度数。
解:设这个等腰三角形的顶角的度数是x°,
则底角的度数是2x°
x+2x+2x=180
解得:x=36
故三个内角分别是36 °、72 °、72 °.
36°
72°
72°
5、上题的等腰三角形纸片按如下方式剪开,可以将原三角形分为三个等腰三角形。你能再设计几种不同的分割方法,将原三角形分为三个等腰三角形吗?团队的力量是无穷的!请与同伴交流讨论。
放飞思想,集思广益
36°
72°
36°
36°
36°
72°
36°
36°
36°
36°
72°
36°
36°
36°
72°
72°
72°
36°
36°
72°
36°
72°
36°
36°
36°
72°
72°
72°
72°
18°
18°
18°
18°
54°
54°
36°
18°
54°
36°
72°
18°
54°
丰收喜报
我学到了……
1、等腰三角形的定义、性质、判定;
2、手脑共用好处多;
3、合作交流、集思广益;
4、学以致用最重要;
5、猜想、实验、推理、归纳、应用;
6、……
丰收喜报
等腰三角形,和谐对称美;
等边对等角,三线俱合一;
做人当如是,表里均一致;
内外皆修备,德智并道行。
1、如图,已知AB=AE, BC=ED,∠ABC=∠AED,点F是CD的中点,AF与CD有什么样的位置关系?
C
D
F
A
B
E
提示:连接AC、AD,构造等腰三角形。
利用三角形全等、“三线合一”知识。
2、如图,在ΔAOB中,点C在OA上,点D、E在OB上,且AB∥CD,AD∥CE,AD=AB,试说明:ΔCDE是等腰三角形?
A
O
E
D
C
B
提示:利用“等边对等角”、“等角对等边”以及等腰三角形的定义解题。
3、正三角形因其独特的对称性而极具美感,请你设计几种不同的分割方法,将正三角形分割为四个等腰三角形。
头脑风暴
提示:等边三角形各角相等,都等于60°。
有两条边相等的三角形叫等腰三角形
定 义
等腰三角形是轴对称图形吗?
拿出等腰三角形纸片,折折看,你能发现什么现象?
实践出真知
动手做一做
看我七十二变
聪明的你看明白了吗?
(1)等腰三角形是轴对称图形
(2)∠B=∠C
(3)∠BAD=∠CAD,AD为顶角的平分线
(4)∠ADB=∠ADC=90°,AD为底边上的高
(5)BD=CD,AD为底边上的中线。
现象:
在等腰ΔABC中,已知AB=AC,作顶角平分线
AD,则∠BAD=∠CAD.
言之有理
在ΔABD和ΔACD中,
∵AB=AC,∠BAD=∠CAD,AD=AD
∴ΔABD≌ΔACD(SAS)
∴BD=CD,∠ADB=∠ADC=90?,∠B=∠C
(全等三角形对应边相等,对应角相等)
∴AD是等腰ΔABC的顶角平分线、底边上的中
线、底边上的高;等腰ΔABC的两个底角相等。
1.等腰三角形是轴对称图形。
3.等腰三角形的两个底角相等(也称“等边对等角”)。
2.等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
有两个角相等的三角形是等腰三角形吗?
在ΔABC中,已知∠B=∠C,作顶角的
平分线AD,则∠BAD=∠CAD .
言之有理
在ΔABD和ΔACD中,
∵∠B=∠C,∠BAD=∠CAD,AD=AD
∴ΔABD≌ΔACD(AAS)
∴AB=AC(全等三角形对应边相等)
∴ΔABC是等腰三角形。
1.有两条边相等的三角形是等腰三角形(定义法)。
2.有两个角相等的三角形是等腰三角形(也称“等角对等边”)。
等边三角形是特殊的等腰三角
形,它的三边都相等。
你能发现它的哪些特征?
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形每个角的平分线和这个角的对 边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
3.等边三角形的各内角都相等,都等于60°。
1、如图,是由大小不等的等边三角形组成的图案,请找出它的对称轴。
2、墙上钉了一根木条,小明想检验这根木条是否水平。他拿来一个如图所示的测平仪,在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤。小明将BC边与木条重合,观察此时悬挂重锤的细线是否通过A点就能做出判断。你能说明其中的道理吗?
答:据题意,AD是等腰三角形ABC的中线,根据等腰三角形“三线合一”的性质,AD也是底边BC上的高,即AD⊥BC,如果悬挂重锤的细线通过A点,则说明木条所在直线垂直于铅垂线,即木条水平。
3、如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使A、B到它的距离之和最短。
C
E
D
.
.
4、一个等腰三角形的底角是顶角的2倍,求它的各个内角的度数。
解:设这个等腰三角形的顶角的度数是x°,
则底角的度数是2x°
x+2x+2x=180
解得:x=36
故三个内角分别是36 °、72 °、72 °.
36°
72°
72°
5、上题的等腰三角形纸片按如下方式剪开,可以将原三角形分为三个等腰三角形。你能再设计几种不同的分割方法,将原三角形分为三个等腰三角形吗?团队的力量是无穷的!请与同伴交流讨论。
放飞思想,集思广益
36°
72°
36°
36°
36°
72°
36°
36°
36°
36°
72°
36°
36°
36°
72°
72°
72°
36°
36°
72°
36°
72°
36°
36°
36°
72°
72°
72°
72°
18°
18°
18°
18°
54°
54°
36°
18°
54°
36°
72°
18°
54°
丰收喜报
我学到了……
1、等腰三角形的定义、性质、判定;
2、手脑共用好处多;
3、合作交流、集思广益;
4、学以致用最重要;
5、猜想、实验、推理、归纳、应用;
6、……
丰收喜报
等腰三角形,和谐对称美;
等边对等角,三线俱合一;
做人当如是,表里均一致;
内外皆修备,德智并道行。
1、如图,已知AB=AE, BC=ED,∠ABC=∠AED,点F是CD的中点,AF与CD有什么样的位置关系?
C
D
F
A
B
E
提示:连接AC、AD,构造等腰三角形。
利用三角形全等、“三线合一”知识。
2、如图,在ΔAOB中,点C在OA上,点D、E在OB上,且AB∥CD,AD∥CE,AD=AB,试说明:ΔCDE是等腰三角形?
A
O
E
D
C
B
提示:利用“等边对等角”、“等角对等边”以及等腰三角形的定义解题。
3、正三角形因其独特的对称性而极具美感,请你设计几种不同的分割方法,将正三角形分割为四个等腰三角形。
头脑风暴
提示:等边三角形各角相等,都等于60°。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
