(人教版)高中物理必修二第1部分 第五章 第4节 圆周运动
文档属性
| 名称 | (人教版)高中物理必修二第1部分 第五章 第4节 圆周运动 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-30 22:49:07 | ||
图片预览










文档简介
(共38张PPT)
理解教材新知
把握热点考向
应用创新演练
知识点一
第
4
节
圆周运动
知识点二
考向一
考向二
随堂基础巩固
第
五章
曲线
运动
课时跟踪训练
知识点三
考向三
1.圆周运动是变速运动,匀速圆周运动 是线速度大小处处相同的圆周运动。
2.质点通过的圆弧长度与所用时间的 比值为线速度大小;半径转过的角
度Δθ与所用时间的比值称为角速度,角速度恒定的圆周运动是匀速圆周运动。
3.做匀速圆周运动的物体,经过一周所用的时间叫周期,
物体单位时间内转过的圈数叫转速。
[自学教材]
弧长Δs
所用时间Δt
快慢
切线
2.匀速圆周运动
如果物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
3.注意的问题
匀速圆周运动中的匀速指的是速度的大小即速率不变,不是速度不变。因为速度的方向是时刻变化的,所以匀速圆周运动是变速运动。
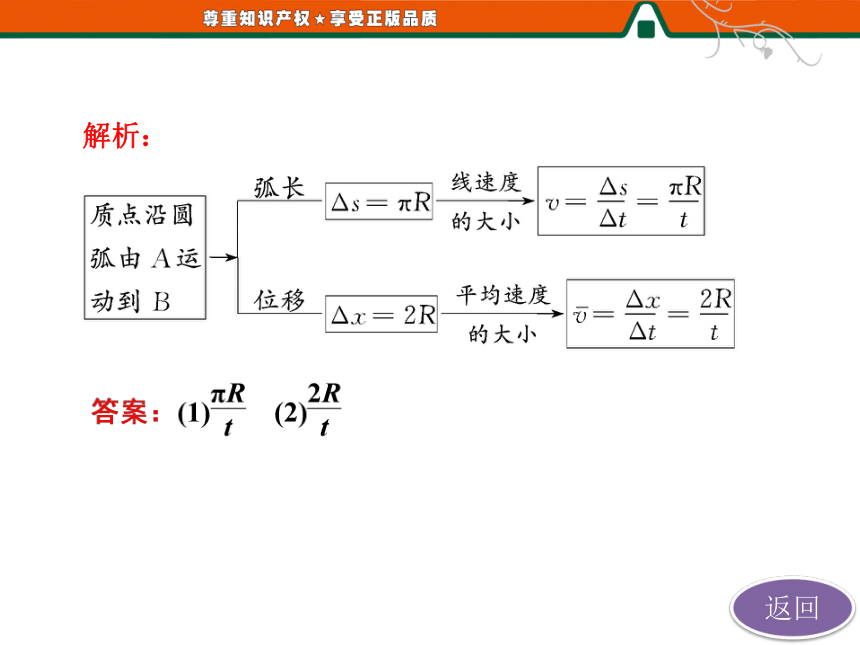
1.如图5-4-1所示,一质点做半径为
R的匀速圆周运动,经过时间t,质点从
A点第一次运动到同一直径上的B点,求:
(1)质点做匀速圆周运动的线速度大小;
(2)质点在时间t内的平均速度大小。
图5-4-1
解析:
[自学教材]
转过的角度Δθ
所用时间Δt
rad/s
不变
2.转速与周期
(1)转速:转速是指物体单位时间 。符号:n表示转速,单位是r/s或r/min。
(2)周期:做匀速圆周运动的物体,经过一周 叫做周期。符号用T表示,单位是秒(s)。
所转过的圈数
所用的时间
2.下列对于匀速圆周运动的说法中,错误的是 ( )
A.线速度不变的运动 B.角速度不变的运动
C.周期不变的运动 D.转速不变的运动
解析:匀速圆周运动是角速度、周期、转速保持不变的运动,其线速度大小不变,方向时刻变化,A错误,B、C、D正确,因此选A。
答案:A
[自学教材]
ωr
角速度大小
半径
[重点诠释]
图5-4-2
图5-4-3
图5-4-4
[特别提醒]
在处理传动装置中各物理量间的关系时,关键是确定其相同的量(线速度或角速度),再由描述圆周运动的各物理量间的关系,确定其他各量间的关系。
3. 如图5-4-5所示的装置中,已知大齿
轮的半径是小齿轮半径的3倍,A点和B点
分别在两轮边缘,C点离大轮轴距离等于
小轮半径。如果不打滑,则它们的线速度
之比vA∶vB∶vC为
A.1∶3∶3 B.1∶3∶1
C.3∶3∶1 D.3∶1∶3
图5-4-5
解析:A、C两点转动的角速度相等,由v=ωr可知,vA∶vC=3∶1;A、B两点的线速度大小相等,即vA∶vB=1∶1,则vA∶vB∶vC=3∶3∶1。答案为C。
答案:C
[例1] 如图5-4-6所示,圆环以直
径AB为轴匀速转动,已知其半径R=0.5 m,
转动周期T=4 s,求环上P点和Q点的角速
度和线速度。
[思路点拨] 整个圆环以AB为轴匀速转动,
环上各点的角速度相同;求线速度,则需找出P点和Q点做圆周运动的半径,利用v=rω求解。
图5-4-6
[答案] 1.57 rad/s 1.57 rad/s 0.39 m/s 0.68 m/s
[借题发挥]
解决此类题目首先要确定质点做圆周运动的轨迹所在的平面,以及圆周运动圆心的位置,从而确定半径,然后由v、ω的定义式及v、ω、R的关系式来计算。
1.如图5-4-7所示是一个玩具陀螺,a、
b和c是陀螺上的三个点。当陀螺绕垂直于
地面的轴线以角速度ω稳定旋转时,下列
表述正确的是 ( )
A.a、b和c三点的线速度大小相等
B.a、b和c三点的角速度相等
C.a、b的角速度比c的大
D.c的线速度比a、b的大
图5-4-7
解析:玩具陀螺以角速度ω绕轴线匀速旋转时,陀螺上各点的角速度均相同,故B正确,C错误;由v=ωr可知,由ra=rb>rc,故va=vb>vc,A、D均错误。
答案:B
[例2] 如图5-4-8所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB。若皮带不打滑,求A、B、C轮边缘的a、b、c三点的角速度之比和线速度之比。
图5-4-8
[思路点拨] 解答本题时应注意以下两个方面:
(1)A、B两轮用皮带传动,线速度相等。
(2)B、C两轮同轴传动,轮上各点的角速度相同。
[答案] 1∶2∶2 1∶1∶2
[解析]
[借题发挥]
(1)“皮带传动”“齿轮传动”“链条传动”三种传动的共同特点是:传动过程中强调皮带、齿轮、链条不打滑,两轮边缘上的每一点的线速度大小相等。由于两轮半径不一定相等,所以两轮转动的角速度不一定相等。
(2)但在同一轮上的各点转动的角速度一定相等,半径不同的各点,线速度不同。
2.如图5-4-9所示,甲、乙、丙三个轮子依靠摩擦传动,
相互之间不打滑,其半径分别为r1、r2、r3。若甲轮的角速度为ω1,则丙轮的角速度为 ( )
答案:A
[例3] 如图5-4-10所示,小球A
在光滑的半径为R的圆形槽内做匀速圆
周运动,当它运动到图中a点时,在圆
形槽中心O点正上方h处,有一小球B沿
Oa方向以某一初速度水平抛出,结果恰
好在a点与A球相碰,求:
(1)B球抛出时的水平初速度。
(2)A球运动的线速度最小值为。
[思路点拨] 题中“在a点与A球相碰”指两球同时到达a点。时间与平抛运动的时间相同,平抛的水平位移等于半径。
图5-4-10
[借题发挥]
此题中圆周运动与平抛运动的联系是时间相等,若考虑到A球做圆周运动的周期性,应考虑到多解的情况,即小球B的飞行时间是小球A的运动周期的整数倍。
在上例条件下,试确定A球做匀速圆周运动的周期的所有可能值。
理解教材新知
把握热点考向
应用创新演练
知识点一
第
4
节
圆周运动
知识点二
考向一
考向二
随堂基础巩固
第
五章
曲线
运动
课时跟踪训练
知识点三
考向三
1.圆周运动是变速运动,匀速圆周运动 是线速度大小处处相同的圆周运动。
2.质点通过的圆弧长度与所用时间的 比值为线速度大小;半径转过的角
度Δθ与所用时间的比值称为角速度,角速度恒定的圆周运动是匀速圆周运动。
3.做匀速圆周运动的物体,经过一周所用的时间叫周期,
物体单位时间内转过的圈数叫转速。
[自学教材]
弧长Δs
所用时间Δt
快慢
切线
2.匀速圆周运动
如果物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
3.注意的问题
匀速圆周运动中的匀速指的是速度的大小即速率不变,不是速度不变。因为速度的方向是时刻变化的,所以匀速圆周运动是变速运动。
1.如图5-4-1所示,一质点做半径为
R的匀速圆周运动,经过时间t,质点从
A点第一次运动到同一直径上的B点,求:
(1)质点做匀速圆周运动的线速度大小;
(2)质点在时间t内的平均速度大小。
图5-4-1
解析:
[自学教材]
转过的角度Δθ
所用时间Δt
rad/s
不变
2.转速与周期
(1)转速:转速是指物体单位时间 。符号:n表示转速,单位是r/s或r/min。
(2)周期:做匀速圆周运动的物体,经过一周 叫做周期。符号用T表示,单位是秒(s)。
所转过的圈数
所用的时间
2.下列对于匀速圆周运动的说法中,错误的是 ( )
A.线速度不变的运动 B.角速度不变的运动
C.周期不变的运动 D.转速不变的运动
解析:匀速圆周运动是角速度、周期、转速保持不变的运动,其线速度大小不变,方向时刻变化,A错误,B、C、D正确,因此选A。
答案:A
[自学教材]
ωr
角速度大小
半径
[重点诠释]
图5-4-2
图5-4-3
图5-4-4
[特别提醒]
在处理传动装置中各物理量间的关系时,关键是确定其相同的量(线速度或角速度),再由描述圆周运动的各物理量间的关系,确定其他各量间的关系。
3. 如图5-4-5所示的装置中,已知大齿
轮的半径是小齿轮半径的3倍,A点和B点
分别在两轮边缘,C点离大轮轴距离等于
小轮半径。如果不打滑,则它们的线速度
之比vA∶vB∶vC为
A.1∶3∶3 B.1∶3∶1
C.3∶3∶1 D.3∶1∶3
图5-4-5
解析:A、C两点转动的角速度相等,由v=ωr可知,vA∶vC=3∶1;A、B两点的线速度大小相等,即vA∶vB=1∶1,则vA∶vB∶vC=3∶3∶1。答案为C。
答案:C
[例1] 如图5-4-6所示,圆环以直
径AB为轴匀速转动,已知其半径R=0.5 m,
转动周期T=4 s,求环上P点和Q点的角速
度和线速度。
[思路点拨] 整个圆环以AB为轴匀速转动,
环上各点的角速度相同;求线速度,则需找出P点和Q点做圆周运动的半径,利用v=rω求解。
图5-4-6
[答案] 1.57 rad/s 1.57 rad/s 0.39 m/s 0.68 m/s
[借题发挥]
解决此类题目首先要确定质点做圆周运动的轨迹所在的平面,以及圆周运动圆心的位置,从而确定半径,然后由v、ω的定义式及v、ω、R的关系式来计算。
1.如图5-4-7所示是一个玩具陀螺,a、
b和c是陀螺上的三个点。当陀螺绕垂直于
地面的轴线以角速度ω稳定旋转时,下列
表述正确的是 ( )
A.a、b和c三点的线速度大小相等
B.a、b和c三点的角速度相等
C.a、b的角速度比c的大
D.c的线速度比a、b的大
图5-4-7
解析:玩具陀螺以角速度ω绕轴线匀速旋转时,陀螺上各点的角速度均相同,故B正确,C错误;由v=ωr可知,由ra=rb>rc,故va=vb>vc,A、D均错误。
答案:B
[例2] 如图5-4-8所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB。若皮带不打滑,求A、B、C轮边缘的a、b、c三点的角速度之比和线速度之比。
图5-4-8
[思路点拨] 解答本题时应注意以下两个方面:
(1)A、B两轮用皮带传动,线速度相等。
(2)B、C两轮同轴传动,轮上各点的角速度相同。
[答案] 1∶2∶2 1∶1∶2
[解析]
[借题发挥]
(1)“皮带传动”“齿轮传动”“链条传动”三种传动的共同特点是:传动过程中强调皮带、齿轮、链条不打滑,两轮边缘上的每一点的线速度大小相等。由于两轮半径不一定相等,所以两轮转动的角速度不一定相等。
(2)但在同一轮上的各点转动的角速度一定相等,半径不同的各点,线速度不同。
2.如图5-4-9所示,甲、乙、丙三个轮子依靠摩擦传动,
相互之间不打滑,其半径分别为r1、r2、r3。若甲轮的角速度为ω1,则丙轮的角速度为 ( )
答案:A
[例3] 如图5-4-10所示,小球A
在光滑的半径为R的圆形槽内做匀速圆
周运动,当它运动到图中a点时,在圆
形槽中心O点正上方h处,有一小球B沿
Oa方向以某一初速度水平抛出,结果恰
好在a点与A球相碰,求:
(1)B球抛出时的水平初速度。
(2)A球运动的线速度最小值为。
[思路点拨] 题中“在a点与A球相碰”指两球同时到达a点。时间与平抛运动的时间相同,平抛的水平位移等于半径。
图5-4-10
[借题发挥]
此题中圆周运动与平抛运动的联系是时间相等,若考虑到A球做圆周运动的周期性,应考虑到多解的情况,即小球B的飞行时间是小球A的运动周期的整数倍。
在上例条件下,试确定A球做匀速圆周运动的周期的所有可能值。
