第1部分 第五章 章末小结 知识整合与阶段检测
文档属性
| 名称 | 第1部分 第五章 章末小结 知识整合与阶段检测 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-30 22:50:57 | ||
图片预览










文档简介
(共31张PPT)
专题归纳例析
阶段质量检测
章末小结
知
识
整
合
与
阶
段
检
测
第
五章
曲线
运动
[特别提醒]
不可伸长的杆或绳,若各点速度不同,则各点速度沿杆或绳方向的投影相同。
[例证1] 河宽60 m,水流速度v=6 m/s,船在静水中速度v2=3 m/s,则:
(1)它渡河的最短时间是多少?
(2)最短航程是多少?
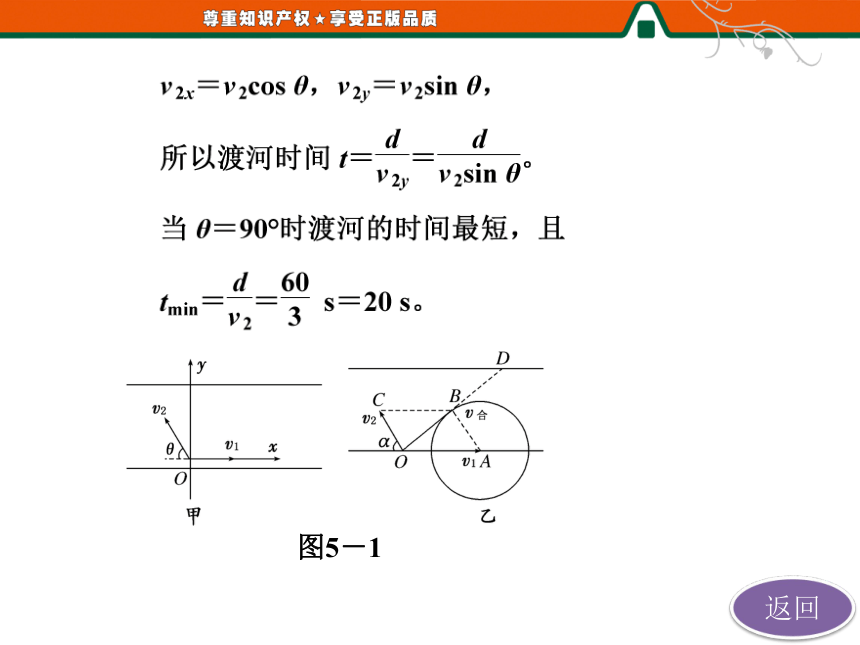
[解析] (1)以水流速度方向为x轴正方向,以垂直河岸方向为y轴正方向,以船开出点为坐标原点建立坐标系,设船与岸成θ角开出(如图5-1甲所示)。将v2沿x、y方向分解:
图5-1
[答案] (1)20 s (2)120 m
图5-2
[例证2] 如图5-3所示,将质量为m的小球从倾角为θ的光滑斜面上A点以速度v0水平抛出(即v0∥CD),小球运动到B点,已知A点的高度为h,求:
图5-3
(1)小球到达B点时的速度大小;
(2)小球到达B点的时间。
专题三 圆周运动的处理方法
(1)明确圆周运动的轨道平面、圆心和半径是解题的基础。分析圆周运动问题时,首先要明确其圆周轨道是怎样的一个平面,确定其圆心在何处,半径是多大,这样才能掌握做圆周运动物体的运动情况。
(2)分析物体受力情况,搞清向心力的来源是解题的关键。如果物体做匀速圆周运动,物体所受各力的合力就是向心力;如果物体做变速圆周运动,它所受的合外力一般不是向心力,但在某些特殊位置(例如:竖直平面内圆周的最高点、最低点),合外力也可能就是向心力。
[例证3] 如图5-4所示,质量分别为M和m的两个小球A、B套在光滑水平直杆P上。整个直杆被固定于竖直转轴上,并保持水平。两球间用劲度系数为k、原长为L的轻质弹簧连接在一起。左边小球被轻质细绳拴在竖直转轴上,细绳长度也为L。现使横杆P随竖直转轴一起在水平面内匀速转动,转动角速度为ω,则当弹簧长度稳定后,细绳的拉力和弹簧的总长度各为多少?
图5-4
图5-5
1.如图5-6所示,当小车A以恒定的速度v向
左运动时,则对于B物体来说,下列说法正
确的是 ( )
A.匀加速上升
B.匀速上升
C.B物体受到的拉力大于B物体受到的重力
D.B物体受到的拉力等于B物体受到的重力
图5-6
答案:C
2.如图5-7所示,关于绳长L一定的圆锥摆,
下列说法正 确的是 ( )
A.摆球的质量越大,则h越大
B.ω越大,则摆角θ也越大
C.ω越大,则h也越大
D.摆球的周期与质量无关
图5-7
答案:BD
3.如图5-8所示,足够长的水平直轨道MN
上左端有一点C,右端有一点D。过MN的
竖直平面上有两点A、B,A点在C点的正上
方,B点与A点在一条水平线上。不计轨道
阻力和空气阻力,下列判断正确的是( )
图5-8
A.在A、C两点以相同的速度同时水平向右抛出两小球,
两球一定会相遇
B.在A、C两点以相同的速度同时水平向右抛出两小球,
两球一定不会相遇
C.在A点水平向右抛出一小球,同时在B点由静止释放一
小球,两球一定会相遇
D.在A、C两点以相同的速度同时水平向右抛出两小球,
并同时在B点由静止释放一小球,三小球有可能在水平轨道上相遇
解析:由于不计轨道阻力和空气阻力,从A点水平抛出的小球做平抛运动,它在水平方向上是匀速直线运动,而在C点抛出的小球沿轨道做匀速直线运动,当A点抛出的小球到达MN轨道时,在水平方向上与C点抛出的小球水平位移相同,它们一定相遇,A正确,B错误;在A点水平向右抛出一小球,同时在B点由静止释放一小球,若A点抛出的小球能到达DB直线上,两小球在竖直方向的位移相同,两球会相遇,若是不能到达DB直线就落到轨道CD上,两球就不会相遇,C错误;由以上分析可知:在A、C两点以相同的速度同时水平向右抛出两小球,并同时在B点由静止释放一小球,三小球有可能在水平轨道上相遇,D正确。
答案:AD
4.从某一高度平抛一物体,若抛出2 s后物体的速度方向与
水平方向成45°角,落地时的速度方向与水平方向成60°角。(取g=10 m/s2)求:
(1)抛出时的速度大小;
(2)落地时的速度大小;
(3)抛出点距地面的高度;
(4)落地时的水平分位移。
专题归纳例析
阶段质量检测
章末小结
知
识
整
合
与
阶
段
检
测
第
五章
曲线
运动
[特别提醒]
不可伸长的杆或绳,若各点速度不同,则各点速度沿杆或绳方向的投影相同。
[例证1] 河宽60 m,水流速度v=6 m/s,船在静水中速度v2=3 m/s,则:
(1)它渡河的最短时间是多少?
(2)最短航程是多少?
[解析] (1)以水流速度方向为x轴正方向,以垂直河岸方向为y轴正方向,以船开出点为坐标原点建立坐标系,设船与岸成θ角开出(如图5-1甲所示)。将v2沿x、y方向分解:
图5-1
[答案] (1)20 s (2)120 m
图5-2
[例证2] 如图5-3所示,将质量为m的小球从倾角为θ的光滑斜面上A点以速度v0水平抛出(即v0∥CD),小球运动到B点,已知A点的高度为h,求:
图5-3
(1)小球到达B点时的速度大小;
(2)小球到达B点的时间。
专题三 圆周运动的处理方法
(1)明确圆周运动的轨道平面、圆心和半径是解题的基础。分析圆周运动问题时,首先要明确其圆周轨道是怎样的一个平面,确定其圆心在何处,半径是多大,这样才能掌握做圆周运动物体的运动情况。
(2)分析物体受力情况,搞清向心力的来源是解题的关键。如果物体做匀速圆周运动,物体所受各力的合力就是向心力;如果物体做变速圆周运动,它所受的合外力一般不是向心力,但在某些特殊位置(例如:竖直平面内圆周的最高点、最低点),合外力也可能就是向心力。
[例证3] 如图5-4所示,质量分别为M和m的两个小球A、B套在光滑水平直杆P上。整个直杆被固定于竖直转轴上,并保持水平。两球间用劲度系数为k、原长为L的轻质弹簧连接在一起。左边小球被轻质细绳拴在竖直转轴上,细绳长度也为L。现使横杆P随竖直转轴一起在水平面内匀速转动,转动角速度为ω,则当弹簧长度稳定后,细绳的拉力和弹簧的总长度各为多少?
图5-4
图5-5
1.如图5-6所示,当小车A以恒定的速度v向
左运动时,则对于B物体来说,下列说法正
确的是 ( )
A.匀加速上升
B.匀速上升
C.B物体受到的拉力大于B物体受到的重力
D.B物体受到的拉力等于B物体受到的重力
图5-6
答案:C
2.如图5-7所示,关于绳长L一定的圆锥摆,
下列说法正 确的是 ( )
A.摆球的质量越大,则h越大
B.ω越大,则摆角θ也越大
C.ω越大,则h也越大
D.摆球的周期与质量无关
图5-7
答案:BD
3.如图5-8所示,足够长的水平直轨道MN
上左端有一点C,右端有一点D。过MN的
竖直平面上有两点A、B,A点在C点的正上
方,B点与A点在一条水平线上。不计轨道
阻力和空气阻力,下列判断正确的是( )
图5-8
A.在A、C两点以相同的速度同时水平向右抛出两小球,
两球一定会相遇
B.在A、C两点以相同的速度同时水平向右抛出两小球,
两球一定不会相遇
C.在A点水平向右抛出一小球,同时在B点由静止释放一
小球,两球一定会相遇
D.在A、C两点以相同的速度同时水平向右抛出两小球,
并同时在B点由静止释放一小球,三小球有可能在水平轨道上相遇
解析:由于不计轨道阻力和空气阻力,从A点水平抛出的小球做平抛运动,它在水平方向上是匀速直线运动,而在C点抛出的小球沿轨道做匀速直线运动,当A点抛出的小球到达MN轨道时,在水平方向上与C点抛出的小球水平位移相同,它们一定相遇,A正确,B错误;在A点水平向右抛出一小球,同时在B点由静止释放一小球,若A点抛出的小球能到达DB直线上,两小球在竖直方向的位移相同,两球会相遇,若是不能到达DB直线就落到轨道CD上,两球就不会相遇,C错误;由以上分析可知:在A、C两点以相同的速度同时水平向右抛出两小球,并同时在B点由静止释放一小球,三小球有可能在水平轨道上相遇,D正确。
答案:AD
4.从某一高度平抛一物体,若抛出2 s后物体的速度方向与
水平方向成45°角,落地时的速度方向与水平方向成60°角。(取g=10 m/s2)求:
(1)抛出时的速度大小;
(2)落地时的速度大小;
(3)抛出点距地面的高度;
(4)落地时的水平分位移。
