苏科版数学八下第8章 认识概率(习题讲评课) 课件(17张)
文档属性
| 名称 | 苏科版数学八下第8章 认识概率(习题讲评课) 课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 324.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 15:49:54 | ||
图片预览





文档简介
(共17张PPT)
初二数学:概率(习题讲评课)
学习目标
1.在具体情境中了解概率的意义,体会概率是描述随机现象的数学模型.
2.知道通过大量的重复试验,可以用频率来估计概率.
3.此外,通过试验,并分析试验结果的活动过程,了解随机现象,培养和发展随机观念.
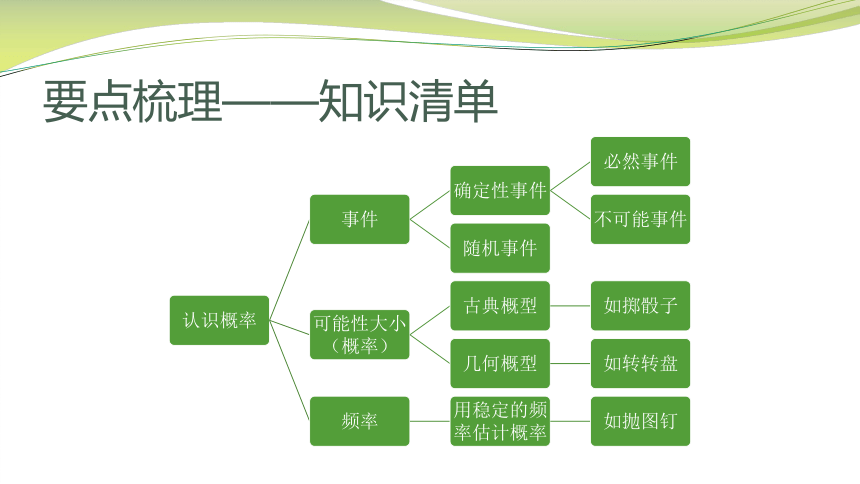
要点梳理——知识清单
要点梳理——知识导练
知识点1:事件
1.判断下列事件是必然事件、不可能事件,还是随机事件:
(1)如果a、b都是实数,那么a+b=b+a;
(2)10张相同的小标签分别标有数字1~10,
从中任意抽取1张,抽到8号签;
(3)同时抛鄉两枚质地均匀的骰子,向上一
面的点数之和为13;
(4)射击1次,中靶.
必然事件
随机事件
不可能事件
随机事件
要点梳理——知识导练
知识点2:可能性大小
2.如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,估计下列事件发生的可能性的大小,并将这些事件的序号按发生的可能性从小到大的顺序排列:
(1)指针落在标有5的区域内;
(2)指针落在标有10的区域内;
(3)指针落在标有偶数或奇数的区城内:
(4)指针落在标有奇数的区城内.
要点梳理——知识导练
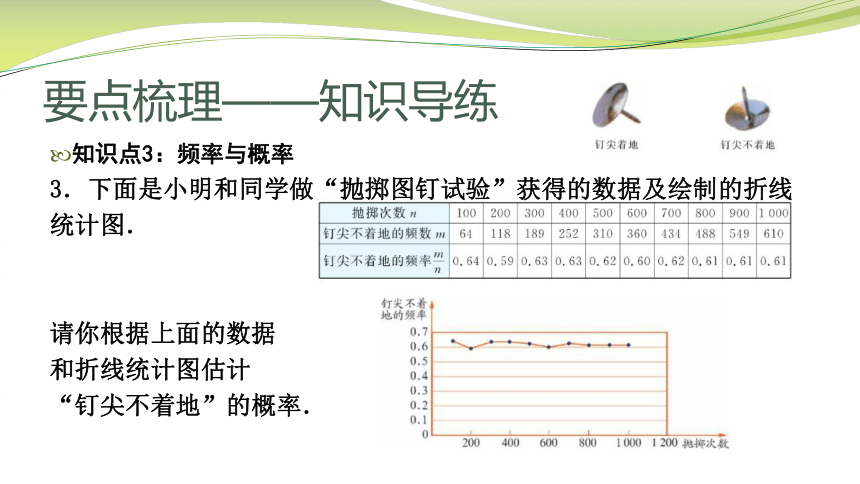
知识点3:频率与概率
3.下面是小明和同学做“抛掷图钉试验”获得的数据及绘制的折线
统计图.
请你根据上面的数据
和折线统计图估计
“钉尖不着地”的概率.
典型例题
例1甲、乙、丙三个事件发生的概率分别为0.5、0.1、0.9.下面的三句话分别描述哪个事件?
(A)发生的可能性很大,但不一定发生:
(B)发生的可能性很小;
(C)发生与不发生的可能性一样大.
0.9
0.1
0.5
典型例题
变式:(辨析)
(1)生活中,为了强调某件事情一定会发生,有人会说“这件事百分之二百会发生”.这句话正确吗?
(2)通常,选择题有4个选择支,其中有且只有1个选择支是正确的.现有20道选择题,小明认为只要在每道题中任选1个选择支,就必有5题的选择结果是正确的.你认为小明的说法正确吗?说说你的理由.
典型例题
例2 一只不透明的袋子中装有1个白球、2个黄球和3个红球,这些球除颜色外都相同,将球摇匀,从中任意摸出1个球.
(1)能事先确定摸到的这个球的颜色吗?
(2)你认为摸到哪种颜色的球的概率最大?
(3)怎样改变袋子中白球、黄球、红球的个数,使摸到这三种颜色的球的概率相等?
不能
红球
调整至三种颜色的球的数量一样多
典型例题
变式:(设计)
(1)在一个小立方体的6个面上分别写上数字1或3、抛掷这个小立方体,使“向上一面的数字为1”比“向上一面的数字为3”出现的可能性大;
(2)设计一个转盘,使转盘停止转动时,“指针落在红色区域”与“指针落在白色区域”出现的可能性一样大.
5个1,1个3
4个1,2个3
……
典型例题
例3 某批乒乓球的质量检验结果如下:
(1)填写表中的空格;
(2)画出优等品频率的折线统计图;
(3)从这批乒乓球中,任意抽取的一只乒乓球是优等品的概率的估计值是多少?
0.960 0.950 0.940 0.942 0.946 0.951 0.949
典型例题
例3
(2)画出优等品
频率的折线统计图;
(3)从这批乒乓球
中,任意抽取的一只
乒乓球是优等品的概
率的估计值是多少?
0.960 0.950 0.940 0.942 0.946 0.951 0.949
练习巩固
1.若气象部门预报明天下雨的概率是65%,下列说法正确的是( ).
A.明天一定会下雨 B.明天一定不会下雨
C.明天下雨的可能性较大 D.明天下雨的可能性较小
2.在一个不透明的箱子中有3张红卡和若干张绿卡,它们除了颜色外其他完全相同,通过多次抽卡试验后发现,抽到绿卡的概率稳定在75%附近,则箱中卡的总张数可能是( ).
A.1张 B.4张 C.9张 D.12张
C
D
练习巩固
3.在4个不透明的袋子中分别装有10个球,其中,1号袋中有10个红球,2号袋中有8个红球.2个白球,3号袋中有5个红球.5个白球,4号袋中有2个红球,8个白球.从各个袋子中任意摸出1个球,摸到白球的可能性最大的是 (填袋子号).
4
练习巩固
4.为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高x(cm)统计如表:
根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于170cm的概率是 .
组别 x<160 160≤x<170 170≤x<180 x≥180
人数 5 38 42 15
0.57
课堂小结
1.必然事件和不可能事件都是确定事件.
2.随机事件发生的可能性有大有小,一个事件发生的可能性大小的数值,称为这个事件发生的概率.
3.在多次重复试验中,一个随机事件发生的频率会在某一个常数附近摆动,并且趋于稳定,人们常把这个常数作为该随机事件发生的概率的估计值.
4.用频率估计一个随机事件发生的概率,必须在相同条件下进行,并且试验的次数要足够多.
THE END
谢谢!
初二数学:概率(习题讲评课)
学习目标
1.在具体情境中了解概率的意义,体会概率是描述随机现象的数学模型.
2.知道通过大量的重复试验,可以用频率来估计概率.
3.此外,通过试验,并分析试验结果的活动过程,了解随机现象,培养和发展随机观念.
要点梳理——知识清单
要点梳理——知识导练
知识点1:事件
1.判断下列事件是必然事件、不可能事件,还是随机事件:
(1)如果a、b都是实数,那么a+b=b+a;
(2)10张相同的小标签分别标有数字1~10,
从中任意抽取1张,抽到8号签;
(3)同时抛鄉两枚质地均匀的骰子,向上一
面的点数之和为13;
(4)射击1次,中靶.
必然事件
随机事件
不可能事件
随机事件
要点梳理——知识导练
知识点2:可能性大小
2.如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,估计下列事件发生的可能性的大小,并将这些事件的序号按发生的可能性从小到大的顺序排列:
(1)指针落在标有5的区域内;
(2)指针落在标有10的区域内;
(3)指针落在标有偶数或奇数的区城内:
(4)指针落在标有奇数的区城内.
要点梳理——知识导练
知识点3:频率与概率
3.下面是小明和同学做“抛掷图钉试验”获得的数据及绘制的折线
统计图.
请你根据上面的数据
和折线统计图估计
“钉尖不着地”的概率.
典型例题
例1甲、乙、丙三个事件发生的概率分别为0.5、0.1、0.9.下面的三句话分别描述哪个事件?
(A)发生的可能性很大,但不一定发生:
(B)发生的可能性很小;
(C)发生与不发生的可能性一样大.
0.9
0.1
0.5
典型例题
变式:(辨析)
(1)生活中,为了强调某件事情一定会发生,有人会说“这件事百分之二百会发生”.这句话正确吗?
(2)通常,选择题有4个选择支,其中有且只有1个选择支是正确的.现有20道选择题,小明认为只要在每道题中任选1个选择支,就必有5题的选择结果是正确的.你认为小明的说法正确吗?说说你的理由.
典型例题
例2 一只不透明的袋子中装有1个白球、2个黄球和3个红球,这些球除颜色外都相同,将球摇匀,从中任意摸出1个球.
(1)能事先确定摸到的这个球的颜色吗?
(2)你认为摸到哪种颜色的球的概率最大?
(3)怎样改变袋子中白球、黄球、红球的个数,使摸到这三种颜色的球的概率相等?
不能
红球
调整至三种颜色的球的数量一样多
典型例题
变式:(设计)
(1)在一个小立方体的6个面上分别写上数字1或3、抛掷这个小立方体,使“向上一面的数字为1”比“向上一面的数字为3”出现的可能性大;
(2)设计一个转盘,使转盘停止转动时,“指针落在红色区域”与“指针落在白色区域”出现的可能性一样大.
5个1,1个3
4个1,2个3
……
典型例题
例3 某批乒乓球的质量检验结果如下:
(1)填写表中的空格;
(2)画出优等品频率的折线统计图;
(3)从这批乒乓球中,任意抽取的一只乒乓球是优等品的概率的估计值是多少?
0.960 0.950 0.940 0.942 0.946 0.951 0.949
典型例题
例3
(2)画出优等品
频率的折线统计图;
(3)从这批乒乓球
中,任意抽取的一只
乒乓球是优等品的概
率的估计值是多少?
0.960 0.950 0.940 0.942 0.946 0.951 0.949
练习巩固
1.若气象部门预报明天下雨的概率是65%,下列说法正确的是( ).
A.明天一定会下雨 B.明天一定不会下雨
C.明天下雨的可能性较大 D.明天下雨的可能性较小
2.在一个不透明的箱子中有3张红卡和若干张绿卡,它们除了颜色外其他完全相同,通过多次抽卡试验后发现,抽到绿卡的概率稳定在75%附近,则箱中卡的总张数可能是( ).
A.1张 B.4张 C.9张 D.12张
C
D
练习巩固
3.在4个不透明的袋子中分别装有10个球,其中,1号袋中有10个红球,2号袋中有8个红球.2个白球,3号袋中有5个红球.5个白球,4号袋中有2个红球,8个白球.从各个袋子中任意摸出1个球,摸到白球的可能性最大的是 (填袋子号).
4
练习巩固
4.为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高x(cm)统计如表:
根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于170cm的概率是 .
组别 x<160 160≤x<170 170≤x<180 x≥180
人数 5 38 42 15
0.57
课堂小结
1.必然事件和不可能事件都是确定事件.
2.随机事件发生的可能性有大有小,一个事件发生的可能性大小的数值,称为这个事件发生的概率.
3.在多次重复试验中,一个随机事件发生的频率会在某一个常数附近摆动,并且趋于稳定,人们常把这个常数作为该随机事件发生的概率的估计值.
4.用频率估计一个随机事件发生的概率,必须在相同条件下进行,并且试验的次数要足够多.
THE END
谢谢!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
