山东省济南市长清区2019-2020学年八年级上学期期末考试数学试题含答案
文档属性
| 名称 | 山东省济南市长清区2019-2020学年八年级上学期期末考试数学试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 790.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 10:09:36 | ||
图片预览

文档简介
八年级质量检测
数学试题
一、选择题(共12题,每题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.化简的结果是( )
A.-3 B.3 C. D.
2.如图,, ,则的度数为( )
A. 115° B.110° C. 105° D.65°
3.下列各点中,位于直角坐标系第二象限的点是( )
A. B. C. D.
4.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.对顶角相等
C.直角的补角仍然是直角 D.同旁内角互补
5.下列各组数值是二元一次方程的解的是( )
A. B. C. D.
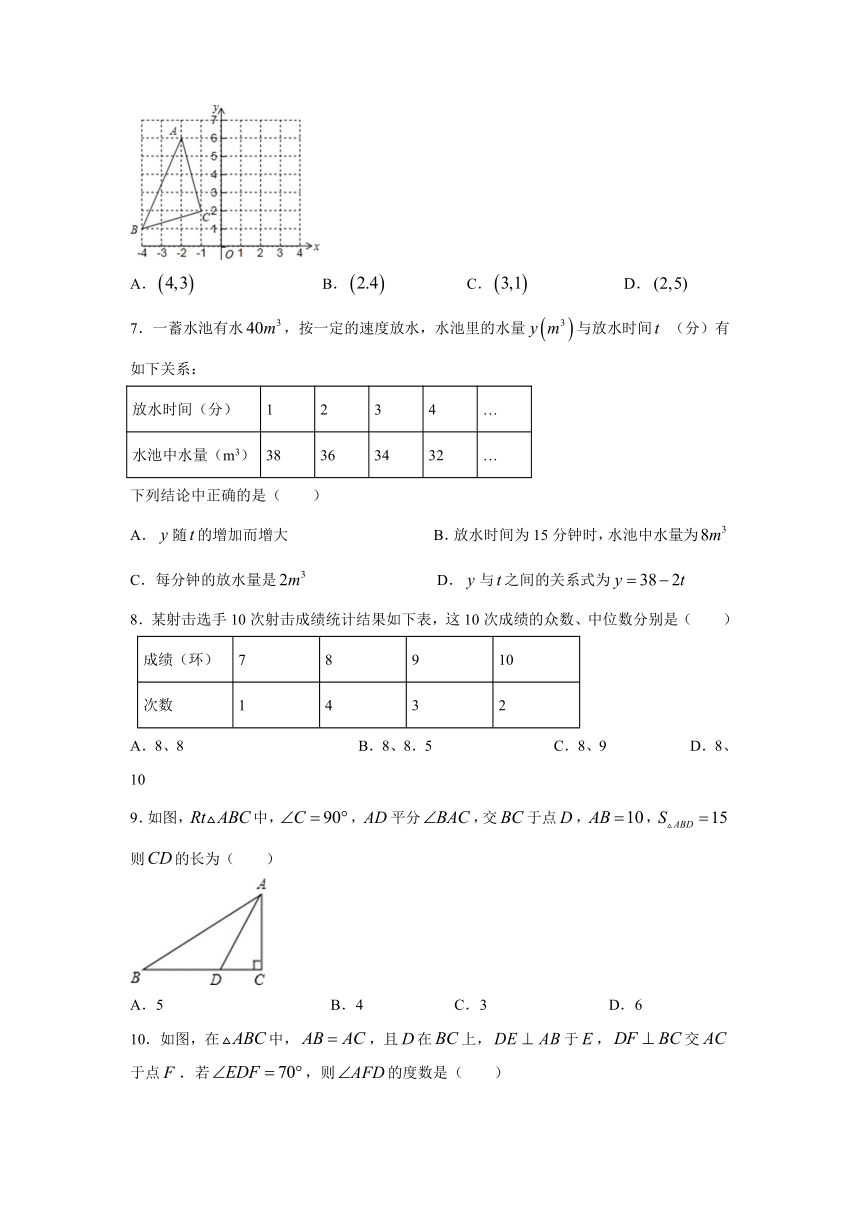
6.如图,在平面直角坐标系中,的顶点都在方格纸的格点上,如果将先向右平移4个单位长度,再向下平移1个单位长度,得到,那么点的对应点的坐标为( )
A. B. C. D.
7.一蓄水池有水,按一定的速度放水,水池里的水量与放水时间 (分)有如下关系:
放水时间(分) 1 2 3 4 …
水池中水量(m3) 38 36 34 32 …
下列结论中正确的是( )
A.随的增加而增大 B.放水时间为15分钟时,水池中水量为
C.每分钟的放水量是 D.与之间的关系式为
8.某射击选手10次射击成绩统计结果如下表,这10次成绩的众数、中位数分别是( )
成绩(环) 7 8 9 10
次数 1 4 3 2
A.8、8 B.8、8.5 C.8、9 D.8、10
9.如图,中,,平分,交于点,, 则的长为( )
A.5 B.4 C.3 D.6
10.如图,在中,,且在上,于,交于点.若,则的度数是( )
A.160° B.150° C.140° D.120°
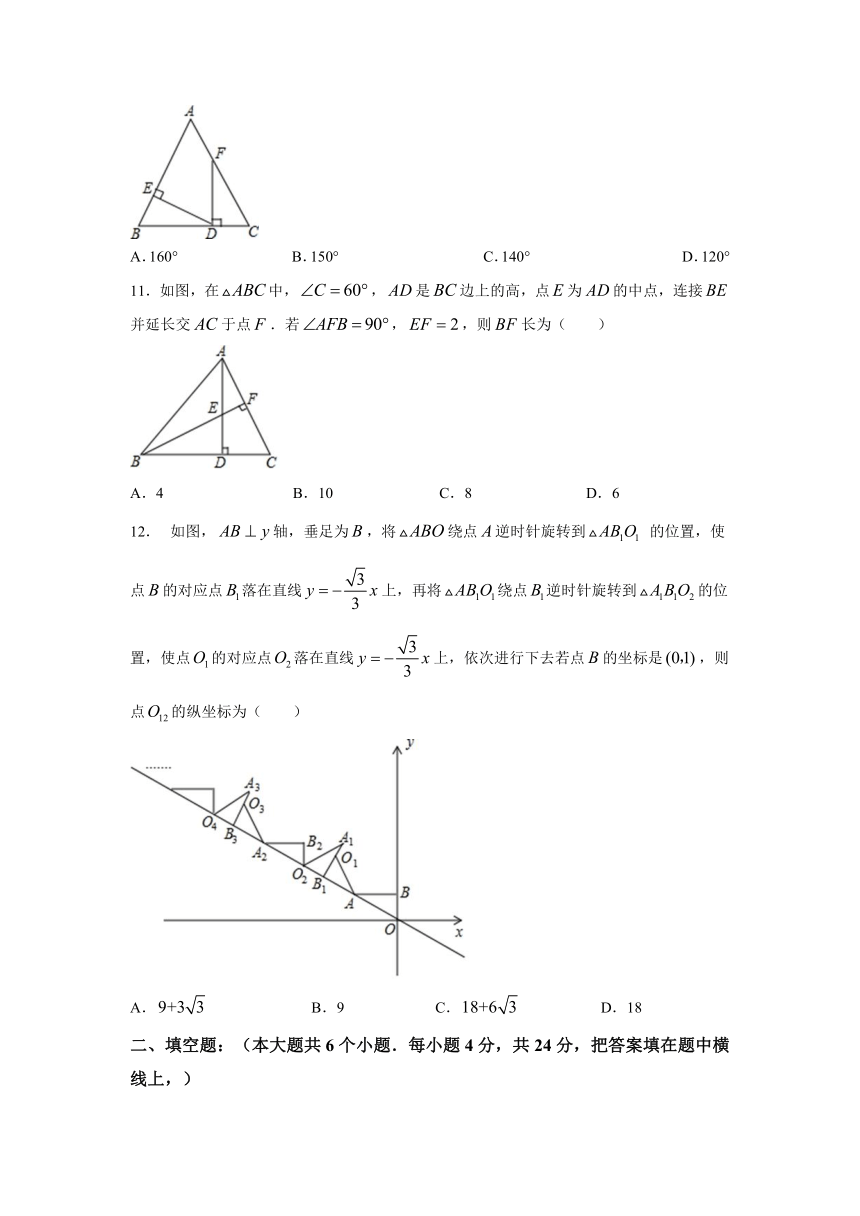
11.如图,在中,,是边上的高,点为的中点,连接并延长交于点.若,,则长为( )
A.4 B.10 C.8 D.6
12. 如图,轴,垂足为,将绕点逆时针旋转到 的位置,使点的对应点落在直线上,再将绕点逆时针旋转到的位置,使点的对应点落在直线上,依次进行下去若点的坐标是,则点的纵坐标为( )
A. B.9 C. D.18
二、填空题:(本大题共6个小题.每小题4分,共24分,把答案填在题中横线上,)
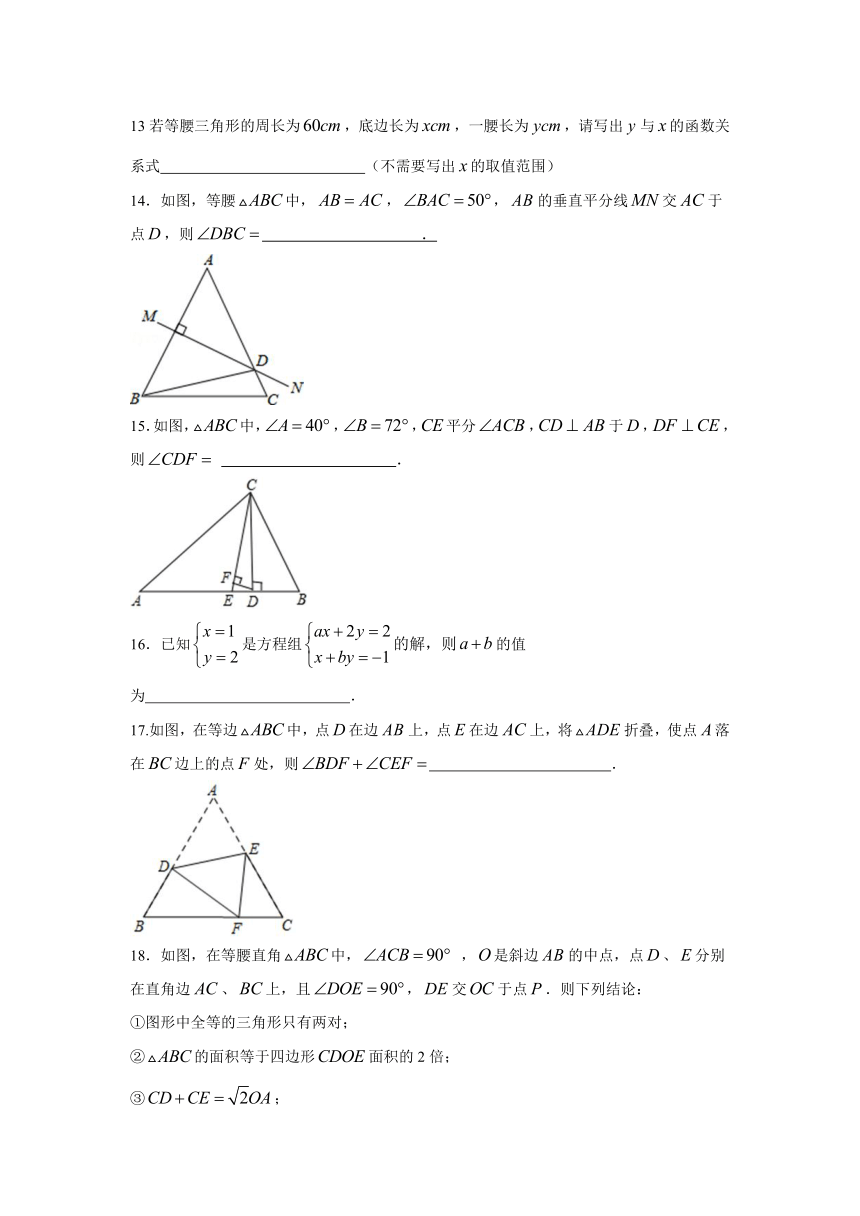
13若等腰三角形的周长为,底边长为,一腰长为,请写出与的函数关系式 (不需要写出的取值范围)
14.如图,等腰中,,,的垂直平分线交于点,则 .
15.如图,中,,,平分,于,,则 .
16.已知是方程组的解,则的值为 .
17.如图,在等边中,点在边上,点在边上,将折叠,使点落在边上的点处,则 .
18.如图,在等腰直角中, ,是斜边的中点,点、分别在直角边、上,且,交于点.则下列结论:
①图形中全等的三角形只有两对;
②的面积等于四边形面积的2倍;
③;
④.
其中正确的结论有 (填序号)
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程成演算步骤)
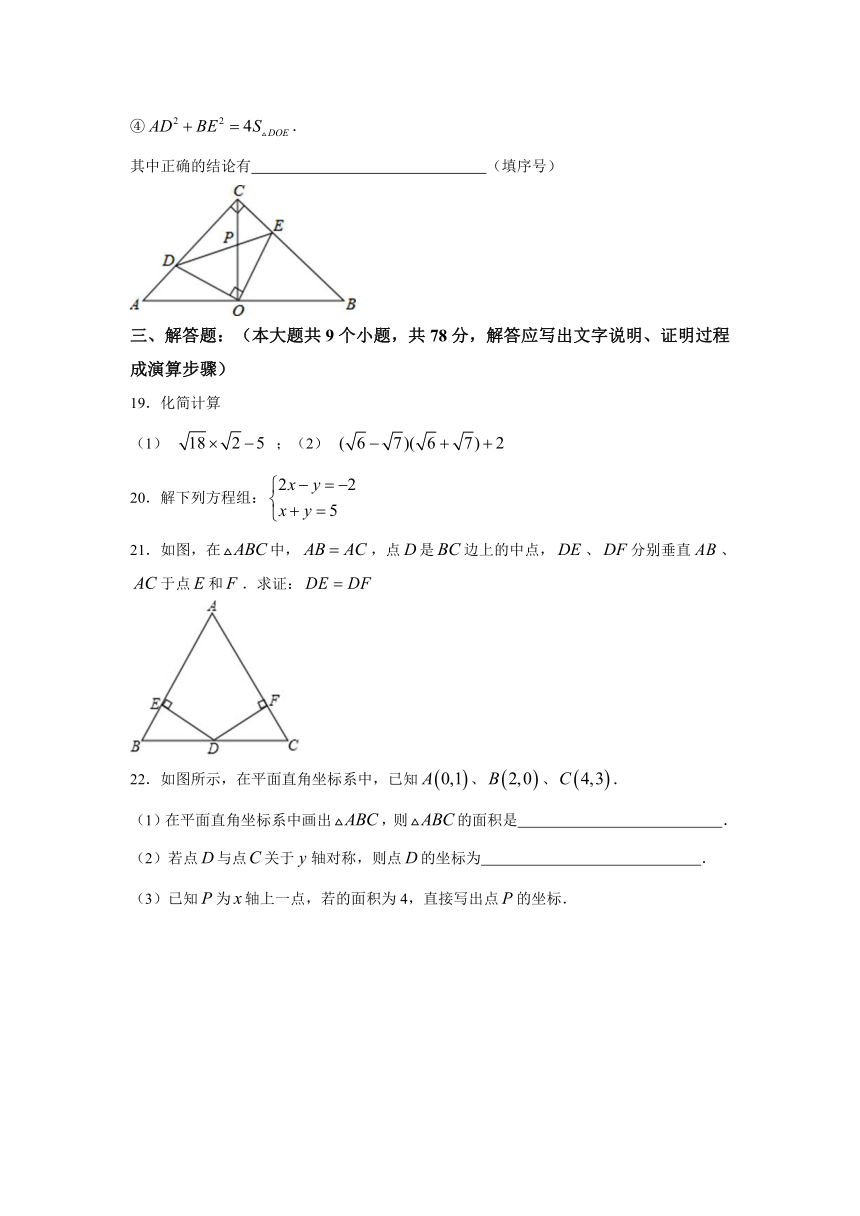
19.化简计算
(1) ;(2)
20.解下列方程组:
21.如图,在中,,点是边上的中点,、分别垂直、于点和.求证:
22.如图所示,在平面直角坐标系中,已知、、.
(1)在平面直角坐标系中画出,则的面积是 .
(2)若点与点关于轴对称,则点的坐标为 .
(3)已知为轴上一点,若的面积为4,直接写出点的坐标.
23.为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用300元购进甲、乙两种节能灯共计100只,很快售完,这两种节能灯的进价、售价如下表:
进价(元/只) 售价(元/只)
甲种节能灯 30 40
乙种节能灯 35 50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
24.某中学为调查本校学生固末平均每天做作业所用时间的情况,随机词查了0名同字,如图是根据调查所得数据绘制的统计图的一部分.请根据以上信息,解答下列问题
(1)请你补全条形统计图
(2)在这次调查的数据中,做作业所用时间的众数是 小时,中位数是 小时,平均数是 小时;
(3)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天组作业时间在3小时内(含3小时)的同学共有多少人?
25. 一条笔直的公路上有甲、乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地设他们同时出发,运动的时间为(分),与乙地的距离为(米),图中线段EF,折线分别表示两人与乙地距离和运动时间之间的函数关系图象
(1)李越骑车的速度为 米/分钟;F点的坐标为 ;
(2)求李越从乙地骑往甲地时, 与之间的函数表达式;
(3)求王明从甲地到乙地时, 与之间的函数表达式;
(4)求李越与王明第二次相遇时的值.
26. 如图,在中,,,点在线段上运动(不与重合),连接,作,交线段于.
(1)当时, °;点从向运动时,逐渐变 .(填“大”或“小”);
(2)当等于多少时,,请说明理由;
(3)在点的运动过程中,的形状也在改变,判断当等于多少度时,是等腰三角形.
27.在平面直角坐标系中,直线与轴交于点 ,与轴交于点,与直线:交于点.
(1)当直线解析式为时,如图1
①求点的坐标:
②根据图象求出当满足什么条件时.
(2)如图2,作的平分线,若,垂足为,的面积为9,且.,分别为线段、上的动点,连接与,试探索 是否存在最小值?若存在,求出这个最小值:若不存在,说明理由.
八年级阶段检测
数学试题(答案)
一、选择题(共12题,每题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B A D D A D C B C A B A
二、填空题:(本大题共6个小题.每小题4分,共24分.把答案填在题中横线上.)
13. 14.15 15. 74.16. —3 . 17. 120 18.②③④.
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤)
19.(1) =6-5 =1 (2)=6-7+2 =1
20.解:(1),
①+②得:3x=3,
解得:x=1
把x=1代入②得:y=4,
所以方程组的解为:
21.证法一:连接AD.
∵AB=AC,点D是BC边上的中点
∴AD平分∠BAC(等腰三角形三线合一性质),
∵DE、DF分别垂直AB、AC于点E和F.
∴DE=DF(角平分线上的点到角两边的距离相等).
证法二:在△ABC中,
∵AB=AC
∴∠B=∠C(等边对等角)
∵点D是BC边上的中点
∴BD=DC
∵DE、DF分别垂直AB、AC于点E和F
∴∠BED=∠CFD=90°
在△BED和△CFD中
∵,
∴△BED≌△CFD(AAS)
∴DE=DF(全等三角形的对应边相等)
22. 解:(1)如图所示作图:
△ABC的面积是:3×4﹣×1×2﹣×2×4﹣×2×3=4;故答案为:4;
(2)(﹣4,3);
(3)(10,0)或(﹣6,0).
23.解:(1)设商场购进甲种节能灯x只,购进乙种节能灯y只,
根据题意得:,
解得:.
答:商场购进甲种节能灯40只,购进乙种节能灯60只.
(2)40×(40﹣30)+60×(50﹣35)=1300(元).
答:商场共计获利1300元.
24.(1)每天作业用时是4小时的人数是:50﹣6﹣12﹣16﹣8=8(人),如图
众数是3小时,中位数是3小时,平均数是3小时;
(2)1500×=1020(人).
25.(1)解: 240;(25,0);
(2)设李越从乙地骑往甲地时,s与t之间的函数表达式为s=kt,2400=10k,得k=240,
即李越从乙地骑往甲地时,s与t之间的函数表达式为s=240t
(3)设王明从甲地到乙地时,s与t之间的函数表达式为s=kt+2400,根据题意得,
25k+2400=0,解得k=﹣96, 所以王明从甲地到乙地时,s与t之间的函数表达式
为:s=﹣96x+2400;
(4)根据题意得,240(t﹣2)﹣96t=2400,解得t=20.
26. (1)115°;小.
(2)当DC=2时,△ABD≌△DCE,
∵ ∠EDC+∠EDA+∠ADB=180°,
∠DAB+∠B+∠ADB=180°,
∠B=∠EDA=40°,
∴∠EDC=∠DAB.
∵∠B=∠C,
DC=AB=2
∴△ABD≌△DCE.
(3)∠BDA=110°或∠BDA=80°
27.解:(1)①由題意,
解得:
所以C(4,4)
②x >4;
(2)由题意,在OC上截取OM=OP,连结MQ,
∵ON平分∠AOC,
∴∠A0Q=∠COQ,
又0Q=0Q.
∴△P0Q≌△M0Q(SAS),
∴PQ=MQ,
∴AQ+PQ=AQ+MQ,
当A、Q、M在同一直銭上,且AM⊥OC吋,AQ+MQ最小,
即AQ+PQ存在最小値;
∴AB⊥ON,所以∠AEO=∠CEO,
..△AEO≌△CEO(ASA),
∴0C=0A=6,
∵△OAC的面积为9,
∴0C?AM=9,
∴AM=3,
∴AQ+PQ存在最小值,最小值为3.
数学试题
一、选择题(共12题,每题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.化简的结果是( )
A.-3 B.3 C. D.
2.如图,, ,则的度数为( )
A. 115° B.110° C. 105° D.65°
3.下列各点中,位于直角坐标系第二象限的点是( )
A. B. C. D.
4.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.对顶角相等
C.直角的补角仍然是直角 D.同旁内角互补
5.下列各组数值是二元一次方程的解的是( )
A. B. C. D.
6.如图,在平面直角坐标系中,的顶点都在方格纸的格点上,如果将先向右平移4个单位长度,再向下平移1个单位长度,得到,那么点的对应点的坐标为( )
A. B. C. D.
7.一蓄水池有水,按一定的速度放水,水池里的水量与放水时间 (分)有如下关系:
放水时间(分) 1 2 3 4 …
水池中水量(m3) 38 36 34 32 …
下列结论中正确的是( )
A.随的增加而增大 B.放水时间为15分钟时,水池中水量为
C.每分钟的放水量是 D.与之间的关系式为
8.某射击选手10次射击成绩统计结果如下表,这10次成绩的众数、中位数分别是( )
成绩(环) 7 8 9 10
次数 1 4 3 2
A.8、8 B.8、8.5 C.8、9 D.8、10
9.如图,中,,平分,交于点,, 则的长为( )
A.5 B.4 C.3 D.6
10.如图,在中,,且在上,于,交于点.若,则的度数是( )
A.160° B.150° C.140° D.120°
11.如图,在中,,是边上的高,点为的中点,连接并延长交于点.若,,则长为( )
A.4 B.10 C.8 D.6
12. 如图,轴,垂足为,将绕点逆时针旋转到 的位置,使点的对应点落在直线上,再将绕点逆时针旋转到的位置,使点的对应点落在直线上,依次进行下去若点的坐标是,则点的纵坐标为( )
A. B.9 C. D.18
二、填空题:(本大题共6个小题.每小题4分,共24分,把答案填在题中横线上,)
13若等腰三角形的周长为,底边长为,一腰长为,请写出与的函数关系式 (不需要写出的取值范围)
14.如图,等腰中,,,的垂直平分线交于点,则 .
15.如图,中,,,平分,于,,则 .
16.已知是方程组的解,则的值为 .
17.如图,在等边中,点在边上,点在边上,将折叠,使点落在边上的点处,则 .
18.如图,在等腰直角中, ,是斜边的中点,点、分别在直角边、上,且,交于点.则下列结论:
①图形中全等的三角形只有两对;
②的面积等于四边形面积的2倍;
③;
④.
其中正确的结论有 (填序号)
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程成演算步骤)
19.化简计算
(1) ;(2)
20.解下列方程组:
21.如图,在中,,点是边上的中点,、分别垂直、于点和.求证:
22.如图所示,在平面直角坐标系中,已知、、.
(1)在平面直角坐标系中画出,则的面积是 .
(2)若点与点关于轴对称,则点的坐标为 .
(3)已知为轴上一点,若的面积为4,直接写出点的坐标.
23.为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用300元购进甲、乙两种节能灯共计100只,很快售完,这两种节能灯的进价、售价如下表:
进价(元/只) 售价(元/只)
甲种节能灯 30 40
乙种节能灯 35 50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
24.某中学为调查本校学生固末平均每天做作业所用时间的情况,随机词查了0名同字,如图是根据调查所得数据绘制的统计图的一部分.请根据以上信息,解答下列问题
(1)请你补全条形统计图
(2)在这次调查的数据中,做作业所用时间的众数是 小时,中位数是 小时,平均数是 小时;
(3)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天组作业时间在3小时内(含3小时)的同学共有多少人?
25. 一条笔直的公路上有甲、乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地设他们同时出发,运动的时间为(分),与乙地的距离为(米),图中线段EF,折线分别表示两人与乙地距离和运动时间之间的函数关系图象
(1)李越骑车的速度为 米/分钟;F点的坐标为 ;
(2)求李越从乙地骑往甲地时, 与之间的函数表达式;
(3)求王明从甲地到乙地时, 与之间的函数表达式;
(4)求李越与王明第二次相遇时的值.
26. 如图,在中,,,点在线段上运动(不与重合),连接,作,交线段于.
(1)当时, °;点从向运动时,逐渐变 .(填“大”或“小”);
(2)当等于多少时,,请说明理由;
(3)在点的运动过程中,的形状也在改变,判断当等于多少度时,是等腰三角形.
27.在平面直角坐标系中,直线与轴交于点 ,与轴交于点,与直线:交于点.
(1)当直线解析式为时,如图1
①求点的坐标:
②根据图象求出当满足什么条件时.
(2)如图2,作的平分线,若,垂足为,的面积为9,且.,分别为线段、上的动点,连接与,试探索 是否存在最小值?若存在,求出这个最小值:若不存在,说明理由.
八年级阶段检测
数学试题(答案)
一、选择题(共12题,每题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B A D D A D C B C A B A
二、填空题:(本大题共6个小题.每小题4分,共24分.把答案填在题中横线上.)
13. 14.15 15. 74.16. —3 . 17. 120 18.②③④.
三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤)
19.(1) =6-5 =1 (2)=6-7+2 =1
20.解:(1),
①+②得:3x=3,
解得:x=1
把x=1代入②得:y=4,
所以方程组的解为:
21.证法一:连接AD.
∵AB=AC,点D是BC边上的中点
∴AD平分∠BAC(等腰三角形三线合一性质),
∵DE、DF分别垂直AB、AC于点E和F.
∴DE=DF(角平分线上的点到角两边的距离相等).
证法二:在△ABC中,
∵AB=AC
∴∠B=∠C(等边对等角)
∵点D是BC边上的中点
∴BD=DC
∵DE、DF分别垂直AB、AC于点E和F
∴∠BED=∠CFD=90°
在△BED和△CFD中
∵,
∴△BED≌△CFD(AAS)
∴DE=DF(全等三角形的对应边相等)
22. 解:(1)如图所示作图:
△ABC的面积是:3×4﹣×1×2﹣×2×4﹣×2×3=4;故答案为:4;
(2)(﹣4,3);
(3)(10,0)或(﹣6,0).
23.解:(1)设商场购进甲种节能灯x只,购进乙种节能灯y只,
根据题意得:,
解得:.
答:商场购进甲种节能灯40只,购进乙种节能灯60只.
(2)40×(40﹣30)+60×(50﹣35)=1300(元).
答:商场共计获利1300元.
24.(1)每天作业用时是4小时的人数是:50﹣6﹣12﹣16﹣8=8(人),如图
众数是3小时,中位数是3小时,平均数是3小时;
(2)1500×=1020(人).
25.(1)解: 240;(25,0);
(2)设李越从乙地骑往甲地时,s与t之间的函数表达式为s=kt,2400=10k,得k=240,
即李越从乙地骑往甲地时,s与t之间的函数表达式为s=240t
(3)设王明从甲地到乙地时,s与t之间的函数表达式为s=kt+2400,根据题意得,
25k+2400=0,解得k=﹣96, 所以王明从甲地到乙地时,s与t之间的函数表达式
为:s=﹣96x+2400;
(4)根据题意得,240(t﹣2)﹣96t=2400,解得t=20.
26. (1)115°;小.
(2)当DC=2时,△ABD≌△DCE,
∵ ∠EDC+∠EDA+∠ADB=180°,
∠DAB+∠B+∠ADB=180°,
∠B=∠EDA=40°,
∴∠EDC=∠DAB.
∵∠B=∠C,
DC=AB=2
∴△ABD≌△DCE.
(3)∠BDA=110°或∠BDA=80°
27.解:(1)①由題意,
解得:
所以C(4,4)
②x >4;
(2)由题意,在OC上截取OM=OP,连结MQ,
∵ON平分∠AOC,
∴∠A0Q=∠COQ,
又0Q=0Q.
∴△P0Q≌△M0Q(SAS),
∴PQ=MQ,
∴AQ+PQ=AQ+MQ,
当A、Q、M在同一直銭上,且AM⊥OC吋,AQ+MQ最小,
即AQ+PQ存在最小値;
∴AB⊥ON,所以∠AEO=∠CEO,
..△AEO≌△CEO(ASA),
∴0C=0A=6,
∵△OAC的面积为9,
∴0C?AM=9,
∴AM=3,
∴AQ+PQ存在最小值,最小值为3.
同课章节目录
