六年级上册数学课件-同步培优 分数巧求和 苏教版 (共21张PPT)
文档属性
| 名称 | 六年级上册数学课件-同步培优 分数巧求和 苏教版 (共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 11:23:08 | ||
图片预览








文档简介
(共21张PPT)
5、分数巧求和
一个分数,如果分子是1,分母能分解成两个连续的自然数的乘积,我们就可以进行如下拆分。
这样可得分数的拆分公式1:
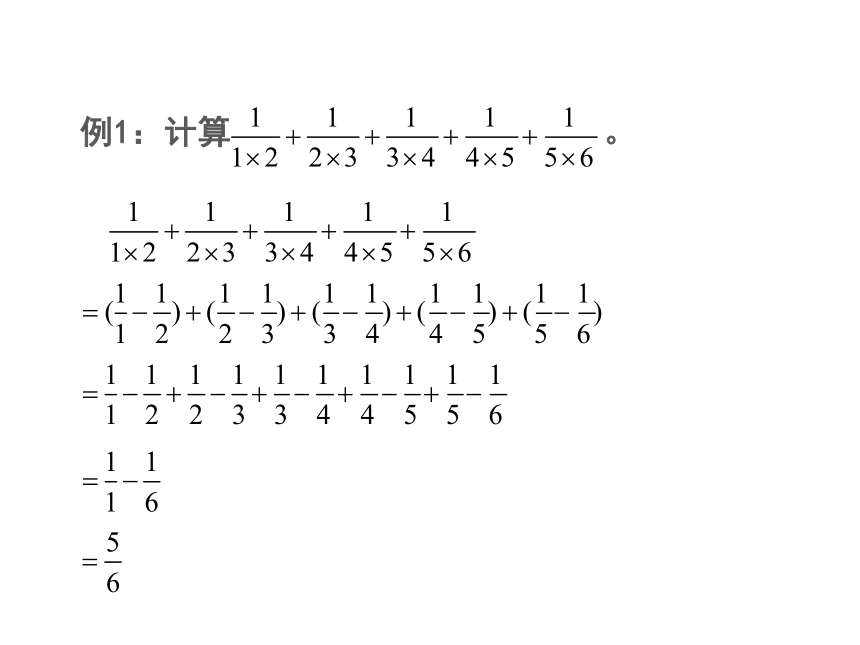
例1:计算 。
在分数计算时,有的计算如果运用通分等思想,由于题目过于复杂,不容易计算。而此时用分数的拆分方法就能使许多项进行加减抵消,使计算更为简便。
一个分数,如果分子是1,分母能分解成两个自然数的乘积,这两个自然数的差是2,也可以进行拆分。
这样可得分数的拆分公式2:
例2:计算 。
例3:计算 。
在将分母进行分解时,我们尽量使上一个分母
分解的大数与后一个分母分解的小数相同,形
成“首尾相连”。
例3:计算 。
一个分数,分母能分解成两个自然数的乘积,但分子不是1,这样的分数,也可以进行拆分。
例4:计算 。
这道题的分数与前面的分数有什么不同?
分析:它的分子不是1,而是2。也就意味着它与分子是1的同分母分数是有倍数关系的,它是分子为1的分数的2倍。
例如: 我们可以把它看做是 。
例4:计算 。
例5:计算 。
例5:计算 。
例6:计算 。
例7:在下面的括号内填上适当的自然数,使等式成立。
例7:在下面的括号内填上适当的自然数,使等式成立。
分析: 可以看成是由 约分得到的。
本题答案不唯一,例如:
分数的拆分:
(1)利用分数拆分公式将异分母的分数进行拆分,使拆分后的一些分数互相抵消,达到简化计算的目的。
拆分公式如下:
(2)利用分数的性质将一个分数单位拆分为几个分数的和的形式。
5、分数巧求和
一个分数,如果分子是1,分母能分解成两个连续的自然数的乘积,我们就可以进行如下拆分。
这样可得分数的拆分公式1:
例1:计算 。
在分数计算时,有的计算如果运用通分等思想,由于题目过于复杂,不容易计算。而此时用分数的拆分方法就能使许多项进行加减抵消,使计算更为简便。
一个分数,如果分子是1,分母能分解成两个自然数的乘积,这两个自然数的差是2,也可以进行拆分。
这样可得分数的拆分公式2:
例2:计算 。
例3:计算 。
在将分母进行分解时,我们尽量使上一个分母
分解的大数与后一个分母分解的小数相同,形
成“首尾相连”。
例3:计算 。
一个分数,分母能分解成两个自然数的乘积,但分子不是1,这样的分数,也可以进行拆分。
例4:计算 。
这道题的分数与前面的分数有什么不同?
分析:它的分子不是1,而是2。也就意味着它与分子是1的同分母分数是有倍数关系的,它是分子为1的分数的2倍。
例如: 我们可以把它看做是 。
例4:计算 。
例5:计算 。
例5:计算 。
例6:计算 。
例7:在下面的括号内填上适当的自然数,使等式成立。
例7:在下面的括号内填上适当的自然数,使等式成立。
分析: 可以看成是由 约分得到的。
本题答案不唯一,例如:
分数的拆分:
(1)利用分数拆分公式将异分母的分数进行拆分,使拆分后的一些分数互相抵消,达到简化计算的目的。
拆分公式如下:
(2)利用分数的性质将一个分数单位拆分为几个分数的和的形式。
