人教A版高二数学选修2-2导数的概念课件(38张ppt)
文档属性
| 名称 | 人教A版高二数学选修2-2导数的概念课件(38张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-03 10:55:48 | ||
图片预览










文档简介
(共38张PPT)
高二年级 数学
导数的概念
高台跳水运动员的平均速度与瞬时速度之间的关系
问题:若高台跳水运动员相对于水面的高度 (单位:米)
与起跳后的时间 (单位:秒)的关系为
如何求运动员在 时的瞬时速度呢?
高台跳水运动员在某一时刻的瞬时速度
请同学们提出解决问题方案、设计探究思路、提炼研究结果.
根据函数关系 可知运动员的初速度为 (m/s), 运动员到达最高点时的速度为零,所以运动员从起跳到达最高点所用的时间
,所以 时,运动员在下落,
利用公式得
所以 时,运动员的瞬时速度为 (m/s).
高台跳水运动员在 时的瞬时速度
极短的一段时间内的平均速度可以近似认为是瞬时速度.
高台跳水运动员的平均速度与瞬时速度之间的关系
解决问题的基本过程
解决问题方案
选取一段时间
建立瞬时速度与平均速度的关系
计算平均速度
发现规律
得到结论
多角度探究
观察分析
发现规律
准确表达
高台跳水运动员的平均速度与瞬时速度之间的关系
解决问题的基本过程
解决问题方案
选取一段时间
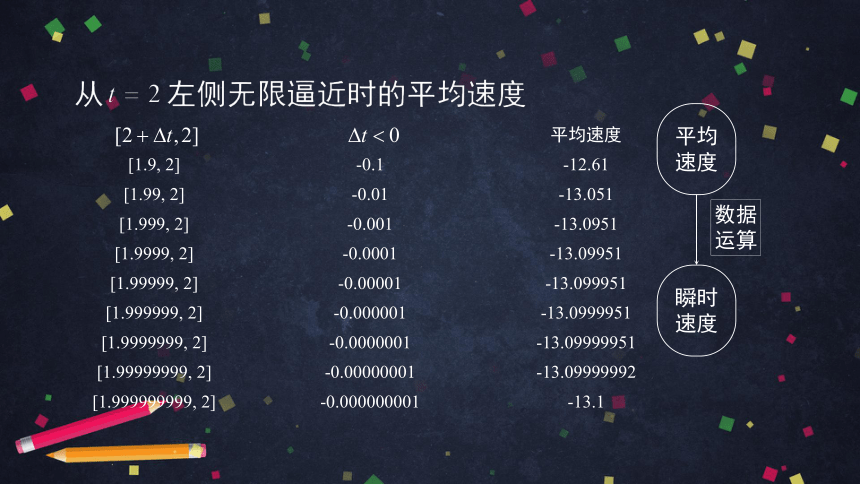
高台跳水运动员在某一时刻附近的平均速度
求平均速度
平均速度
[1.9, 2] -0.1 -12.61
[1.99, 2] -0.01 -13.051
[1.999, 2] -0.001 -13.0951
[1.9999, 2] -0.0001 -13.09951
[1.99999, 2] -0.00001 -13.099951
[1.999999, 2] -0.000001 -13.0999951
[1.9999999, 2] -0.0000001 -13.09999951
[1.99999999, 2] -0.00000001 -13.09999992
[1.999999999, 2] -0.000000001 -13.1
平均速度
数据
运算
瞬时速度
解决问题的基本过程
解决问题方案
选取一段时间
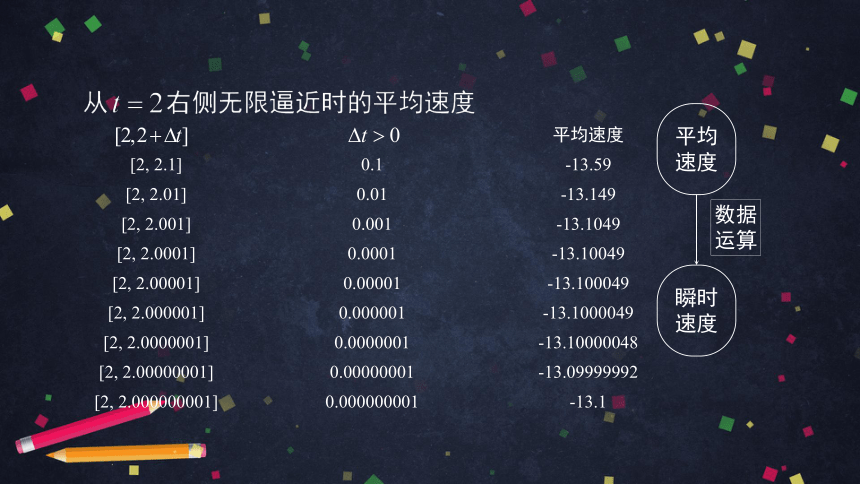
高台跳水运动员在某一时刻附近的平均速度
求平均速度
观察分析
平均速度
[2, 2.1] 0.1 -13.59
[2, 2.01] 0.01 -13.149
[2, 2.001] 0.001 -13.1049
[2, 2.0001] 0.0001 -13.10049
[2, 2.00001] 0.00001 -13.100049
[2, 2.000001] 0.000001 -13.1000049
[2, 2.0000001] 0.0000001 -13.10000048
[2, 2.00000001] 0.00000001 -13.09999992
[2, 2.000000001] 0.000000001 -13.1
平均速度
数据
运算
瞬时速度
解决问题的基本过程
解决问题方案
选取一段时间
高台跳水运动员在某一时刻附近的平均速度
求平均速度
观察分析
平均速度
数据
运算
瞬时速度
平均速度
几何直观
瞬时速度
平均速度
几何直观
瞬时速度
平均速度
几何直观
瞬时速度
平均速度
瞬时速度
几何
直观
数据
运算
代数式
化简
高台跳水运动员在某一时刻的瞬时速度
平均速度
瞬时速度
几何
直观
数据
运算
代数式
化简
高台跳水运动员在某一时刻的瞬时速度
多角度探究
观察分析
发现规律
准确表达
当时间变化量无限趋近于0时,平均速度的极限值即为瞬时速度.
多角度探究
观察分析
发现规律
准确表达
高台跳水运动员在某一时刻的瞬时速度
具体
一般
高台跳水运动员在某一时刻的瞬时速度
瞬时变化
瞬时速度
平均变化率
瞬时变化率
具体
一般
平均变化率与瞬时变化率的定义
瞬时变化率
抽象概括,形成概念
应用概念:求函数在某点处的导数
分析:首先计算该点附近的平均变化率
然后求其极限
得到该点处的导数值.
应用概念:求函数在某点处的导数
作差、作比
得到平均变化率
解:
取极限,得到瞬时变化率
应用概念:求函数在某点处的导数
导数值
平均变化率
求函数在某点处的导数的一般步骤
抽象概括,形成概念
抽象概括,形成概念
应用概念:求函数的导函数
分析:首先计算平均变化率
然后求其极限
得到函数的导数.
平均变化率
应用概念:求函数的导函数
平均变化率
瞬时变化率
导函数
应用概念:求函数的导函数
求函数的导函数的一般步骤
函数
导数概念
物理意义
物理运动
数学抽象
直观想象
几何意义
本节课研究问题的方法
本节课你学到了什么?
课堂小结
你是如何获得这些知识的?
研究问题的步骤:提出问题、寻求想法、确定方法、
实施操作、发现规律.本着用已知探究未知的方式,
探究过程体会了无限逼近的数学思想.
平均变化率、瞬时变化率、导数的概念;
从特殊到一般,从具体到抽象;
通过本节课学习,谈谈你的体会.
丰富实例
数学情境
物理情境
医药情境
函数
从感性具体
到理性抽象
从平均变化率
到瞬时变化率
运动变化观点
与极限思想
导数
认知规律
思想方法
数学抽象
直观想象
经历
领悟
把握
……
阅读导数形成与发展的历史资料
作业
求函数 的导数.
求函数 的导数.
高二年级 数学
导数的概念
高台跳水运动员的平均速度与瞬时速度之间的关系
问题:若高台跳水运动员相对于水面的高度 (单位:米)
与起跳后的时间 (单位:秒)的关系为
如何求运动员在 时的瞬时速度呢?
高台跳水运动员在某一时刻的瞬时速度
请同学们提出解决问题方案、设计探究思路、提炼研究结果.
根据函数关系 可知运动员的初速度为 (m/s), 运动员到达最高点时的速度为零,所以运动员从起跳到达最高点所用的时间
,所以 时,运动员在下落,
利用公式得
所以 时,运动员的瞬时速度为 (m/s).
高台跳水运动员在 时的瞬时速度
极短的一段时间内的平均速度可以近似认为是瞬时速度.
高台跳水运动员的平均速度与瞬时速度之间的关系
解决问题的基本过程
解决问题方案
选取一段时间
建立瞬时速度与平均速度的关系
计算平均速度
发现规律
得到结论
多角度探究
观察分析
发现规律
准确表达
高台跳水运动员的平均速度与瞬时速度之间的关系
解决问题的基本过程
解决问题方案
选取一段时间
高台跳水运动员在某一时刻附近的平均速度
求平均速度
平均速度
[1.9, 2] -0.1 -12.61
[1.99, 2] -0.01 -13.051
[1.999, 2] -0.001 -13.0951
[1.9999, 2] -0.0001 -13.09951
[1.99999, 2] -0.00001 -13.099951
[1.999999, 2] -0.000001 -13.0999951
[1.9999999, 2] -0.0000001 -13.09999951
[1.99999999, 2] -0.00000001 -13.09999992
[1.999999999, 2] -0.000000001 -13.1
平均速度
数据
运算
瞬时速度
解决问题的基本过程
解决问题方案
选取一段时间
高台跳水运动员在某一时刻附近的平均速度
求平均速度
观察分析
平均速度
[2, 2.1] 0.1 -13.59
[2, 2.01] 0.01 -13.149
[2, 2.001] 0.001 -13.1049
[2, 2.0001] 0.0001 -13.10049
[2, 2.00001] 0.00001 -13.100049
[2, 2.000001] 0.000001 -13.1000049
[2, 2.0000001] 0.0000001 -13.10000048
[2, 2.00000001] 0.00000001 -13.09999992
[2, 2.000000001] 0.000000001 -13.1
平均速度
数据
运算
瞬时速度
解决问题的基本过程
解决问题方案
选取一段时间
高台跳水运动员在某一时刻附近的平均速度
求平均速度
观察分析
平均速度
数据
运算
瞬时速度
平均速度
几何直观
瞬时速度
平均速度
几何直观
瞬时速度
平均速度
几何直观
瞬时速度
平均速度
瞬时速度
几何
直观
数据
运算
代数式
化简
高台跳水运动员在某一时刻的瞬时速度
平均速度
瞬时速度
几何
直观
数据
运算
代数式
化简
高台跳水运动员在某一时刻的瞬时速度
多角度探究
观察分析
发现规律
准确表达
当时间变化量无限趋近于0时,平均速度的极限值即为瞬时速度.
多角度探究
观察分析
发现规律
准确表达
高台跳水运动员在某一时刻的瞬时速度
具体
一般
高台跳水运动员在某一时刻的瞬时速度
瞬时变化
瞬时速度
平均变化率
瞬时变化率
具体
一般
平均变化率与瞬时变化率的定义
瞬时变化率
抽象概括,形成概念
应用概念:求函数在某点处的导数
分析:首先计算该点附近的平均变化率
然后求其极限
得到该点处的导数值.
应用概念:求函数在某点处的导数
作差、作比
得到平均变化率
解:
取极限,得到瞬时变化率
应用概念:求函数在某点处的导数
导数值
平均变化率
求函数在某点处的导数的一般步骤
抽象概括,形成概念
抽象概括,形成概念
应用概念:求函数的导函数
分析:首先计算平均变化率
然后求其极限
得到函数的导数.
平均变化率
应用概念:求函数的导函数
平均变化率
瞬时变化率
导函数
应用概念:求函数的导函数
求函数的导函数的一般步骤
函数
导数概念
物理意义
物理运动
数学抽象
直观想象
几何意义
本节课研究问题的方法
本节课你学到了什么?
课堂小结
你是如何获得这些知识的?
研究问题的步骤:提出问题、寻求想法、确定方法、
实施操作、发现规律.本着用已知探究未知的方式,
探究过程体会了无限逼近的数学思想.
平均变化率、瞬时变化率、导数的概念;
从特殊到一般,从具体到抽象;
通过本节课学习,谈谈你的体会.
丰富实例
数学情境
物理情境
医药情境
函数
从感性具体
到理性抽象
从平均变化率
到瞬时变化率
运动变化观点
与极限思想
导数
认知规律
思想方法
数学抽象
直观想象
经历
领悟
把握
……
阅读导数形成与发展的历史资料
作业
求函数 的导数.
求函数 的导数.
