人教版数学八年级下册 19.3 课题学习-----选择方案 教案
文档属性
| 名称 | 人教版数学八年级下册 19.3 课题学习-----选择方案 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 81.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 00:00:00 | ||
图片预览


文档简介
19.3 课题学习 选择方案(1)
学习目标:
1.会用一次函数知识解决方案选择问题,体会函数
模型思想;
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方
法.
学习重点:
建立函数模型解决方案选择问题.
教学过程:
提出问题
下表给出A,B,C 三种上宽带网的收费方式:
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25? 0.05?
B 50 50 0.05?
C 120 ???不限时
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?
根据省钱原则选择方案
分析问题
要比较三种收费方式的费用,需要做什么?
分别计算每种方案的费用.
怎样计算费用?
A,B,C 三种方案中,所需要的费用是固定的还
是变化的?
方案C费用固定;
方案A,B的费用在超过一定时间后,随上网时间变化,是上网时间的函数.请分别写出三种方案的上网费用y 元与上网时间th之间的函数解析式.
能把这个问题描述为函数问题吗?
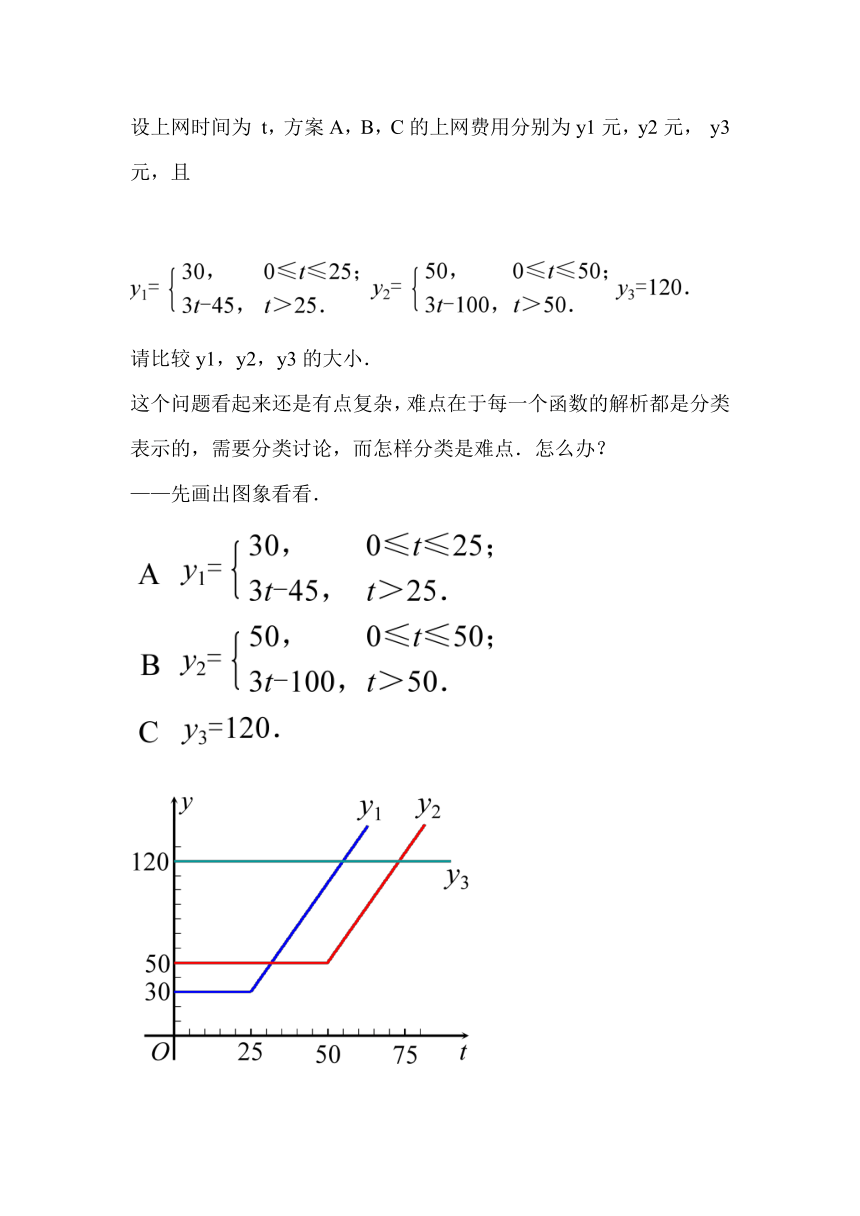
设上网时间为 t,方案A,B,C的上网费用分别为y1元,y2元, y3 元,且
请比较y1,y2,y3的大小.
这个问题看起来还是有点复杂,难点在于每一个函数的解析都是分类表示的,需要分类讨论,而怎样分类是难点.怎么办?
——先画出图象看看.
解决问题
解:设上网时间为t h,方案A,B,C的上网费用分
别为y1 元,y2 元, y3 元,则
结合图象可知:
(1)若y1=y2,即3t-45=50,解方程,得t =;
(2)若y1<y2,即3t-45<50,解不等式,得t<
(3)若y1>y2,即3t-45>50,解不等式,得t>
解:令3t-100=120,解方程,得t =
令3t-100>120,解不等式,得t>
当上网时间不超过31小时40分,选择方案A最省钱;
当上网时间为31小时40分至73小时20分,选择方案B最省钱;
当上网时间超过73小时20分,选择方案C最省钱.
解后反思
这个实际问题的解决过程中是怎样思考的?
课后练习:
1、从A,B两水库向甲乙两地调水,其中甲地需水15万吨,乙地需水13万吨,A,B两水库各可调水14万吨。从A地到甲地50千米,到乙地30千米,从B地到甲地60千米,到乙地45千米。设计一个调运方案,使得水的调运量(单位:万吨 -千米)最小。
设从A水库调往甲地的水量为x万吨,这次调水总的调水量为y万吨-千米。则
y=50x+30(14-x)+60(15-x)+45(x-1)
=5x+1275
由题意可知:(1≤x≤14)当x=1时,y最小=1280(万吨-千米)
课堂小结:
1.一次函数最值问题的解决方法。
2.本节课渗透的数学思想方法。
(建立数学模型、数形结合、分类讨论)
3.本节课的收获:先由学生总结,老师启发补充。
作业布置:
课本第109页 第15题
