华师大版数学八年级上册第12章 整式的乘除 检测卷(含答案)
文档属性
| 名称 | 华师大版数学八年级上册第12章 整式的乘除 检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 50.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 12:59:26 | ||
图片预览



文档简介
华师大版数学八年级上册第12章检测卷
一、选择题(每题3分,共30分)
1.计算(a3)2的结果是( )
A.a5 B.-a5 C.a6 D.-a6
2.下列运算正确的是( )
A.3a2-2a2=1 B.a2·a3=a6 C.(ab)2÷a=b2 D.(-ab)3=-a3b3
3.下列式子从左到右变形是因式分解的是( )
A.3x2-3y2-3xy=3(x+y)(x-y)-3xy
B.(y+2x)2-(x+2y)2=3(x+y)(x-y)
C.3(x+y)(x-y)=3x2-3y2
D.(y+2x)2-(x+2y)2=3x2-3y2
4.多项式a(x2-2x+1)与多项式(x-1)(x+1)的公因式是( )
A.x-1 B.x+1 C.x2+1 D.x2
5.下列计算正确的是( )
A.(2a+3b)(3b-2a)=4a2-9b2 B.(-xy2)2÷(-x2y)=-y3
C.=x2-xy+y2 D.-(-a3b2)÷(-a2b2)=a
6.计算××(-1)2 021的结果是( )
A. B. C.1 D.-1
7.若am=2,an=3,ap=5,则a2m+n-p的值是( )
A.2.4 B.2 C.1 D.0
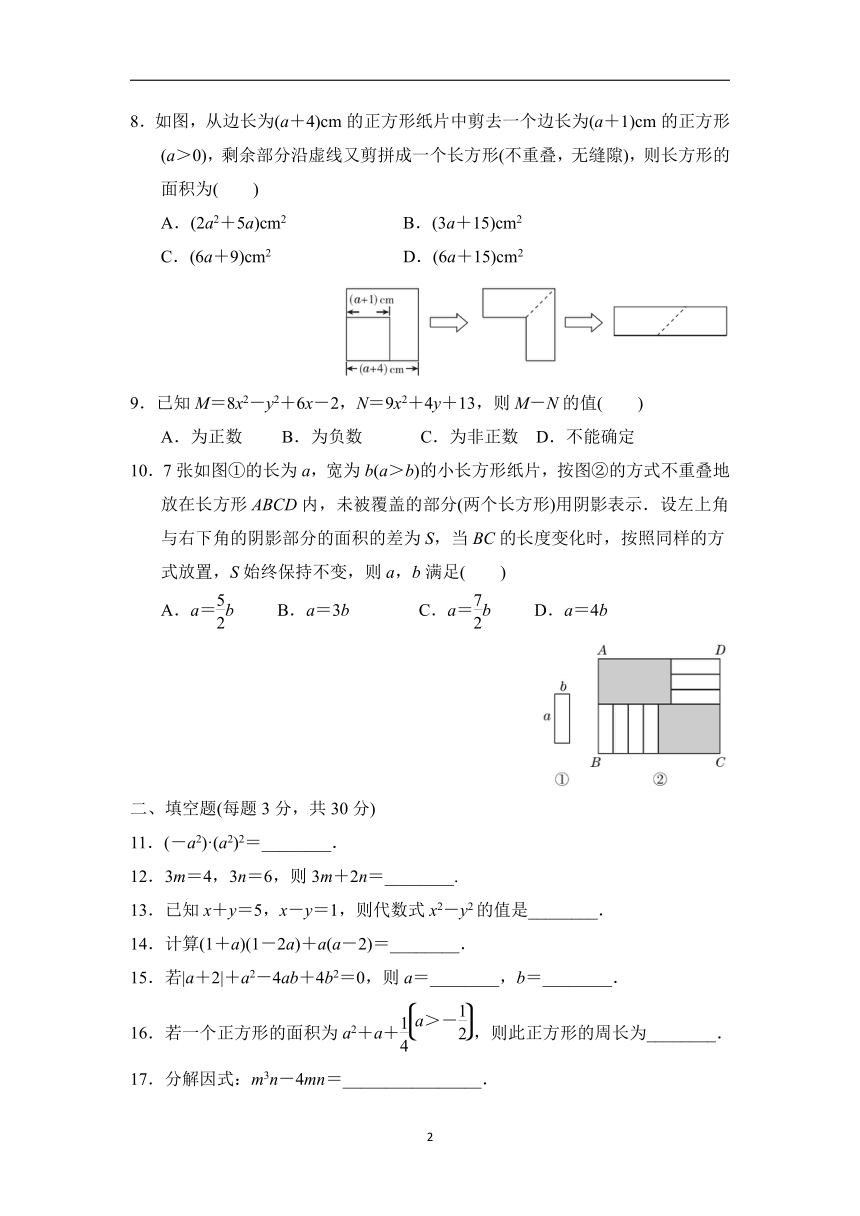
8.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠,无缝隙),则长方形的面积为( )
A.(2a2+5a)cm2 B.(3a+15)cm2
C.(6a+9)cm2 D.(6a+15)cm2
9.已知M=8x2-y2+6x-2,N=9x2+4y+13,则M-N的值( )
A.为正数 B.为负数 C.为非正数 D.不能确定
10.7张如图①的长为a,宽为b(a>b)的小长方形纸片,按图②的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的方式放置,S始终保持不变,则a,b满足( )
A.a=b B.a=3b C.a=b D.a=4b
二、填空题(每题3分,共30分)
11.(-a2)·(a2)2=________.
12.3m=4,3n=6,则3m+2n=________.
13.已知x+y=5,x-y=1,则代数式x2-y2的值是________.
14.计算(1+a)(1-2a)+a(a-2)=________.
15.若|a+2|+a2-4ab+4b2=0,则a=________,b=________.
16.若一个正方形的面积为a2+a+,则此正方形的周长为________.
17.分解因式:m3n-4mn=________________.
18.计算2 021×2 023-2 0222=__________.
19.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成,定义=ad-bc,上述记号就叫做2阶行列式.若=8,则x=________.
20.根据(x-1)(x+1)=x2-1,(x-1)(x2+x+1)=x3-1,(x-1)(x3+x2+x+1)=x4-1,(x-1)(x4+x3+x2+x+1)=x5-1,…的规律,可以得出22 022+22 021+22 020+…+23+22+2+1的末位数字是________.
三、解答题(22,24,25,26题每题6分,21,23题每题8分,27,28题每题10分,共60分)
21.计算:
(1)2a5·(-a)2-(-a2)2·(-7a);
(2)(-a2b2)÷(-ab2)·(-3ab3);
(3)(x-4y)(2x+3y)-(x+2y)(x-y);
(4)[(x+2y)(x-2y)-(2x-y)2+5y2]÷(-2x).
22.先化简,再求值:
(1)(x+5)(x-1)+(x-2)2,其中x=-2;
(2)(m2-6mn+9n2)÷(m-3n)-(4m2-9n2)÷(2m-3n),其中m=-3,n=-.
23.把下列各式分解因式:
(1)6ab3-24a3b; (2)2x2y-8xy+8y;
(3)a2(x-y)+4b2(y-x); (4)4m2n2-(m2+n2)2.
24.已知(x2+px+8)(x2-3x+q)的展开式中不含x2和x3项,求p,q的值.
25.学习了分解因式的知识后,老师提出了这样一个问题:设n为整数,则(n+7)2-(n-3)2的值一定能被20整除吗?若能,请说明理由;若不能,请举出一个反例.
26.已知a,b,c是△ABC的三边长,且a2+2b2+c2-2b(a+c)=0,你能判断△ABC的形状吗?请说明理由.
27.如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间修建一座雕像.
(1)求绿化面积是多少平方米?
(2)求当a=3,b=2时的绿化面积.
28.已知x≠1,(1-x)(1+x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4.
(1)根据以上式子计算:
①(1-2)×(1+2+22+23+24+25);
②2+22+23+…+2n(n为正整数);
③(x-1)(x99+x98+x97+…+x2+x+1).
(2)通过以上计算,请你进行下面的探索:
①(a-b)(a+b)=____________;
②(a-b)(a2+ab+b2)=____________;
③(a-b)(a3+a2b+ab2+b3)=____________.
答案
一、1.C 2.D 3.B 4.A 5.B 6.D
7.A 8.D 9.B 10.B
二、11.-a6 12.144 13.5
14.-a2-3a+1 15.-2;-1
16.4a+2 17.mn(m+2)(m-2)
18.-1 19.2
20.7 解析:由题意可知22 022+22 021+…+22+2+1=(2-1)×(22 022+22 021+…+22+2+1)=22 023-1,而21=2,22=4,23=8,24=16,25=32,26=64,…,可知2n(n为正整数)的末位数字按2,4,8,6的顺序循环,而2 023÷4=505……3,∴22 023的末位数字是8,则22 023-1的末位数字是7.
三、21.解:(1)原式=2a5·a2-a4·(-7a)=2a7+7a5.
(2)原式=a·(-3ab3)=-3a2b3.
(3)原式=2x2+3xy-8xy-12y2-(x2-xy+2xy-2y2)=2x2-5xy-12y2-x2-xy+2y2=x2-6xy-10y2.
(4)原式=[x2-4y2-(4x2-4xy+y2)+5y2]÷(-2x)
=(x2-4y2-4x2+4xy-y2+5y2)÷(-2x)
=(-3x2+4xy)÷(-2x)
=x-2y.
22.解:(1)原式=x2-x+5x-5+x2-4x+4=2x2-1.
当x=-2时,原式=2x2-1=2×(-2)2-1=7.
(2)(m2-6mn+9n2)÷(m-3n)-(4m2-9n2)÷(2m-3n)
=(m-3n)2÷(m-3n)-(2m-3n)(2m+3n)÷(2m-3n)
=m-3n-(2m+3n)
=-m-6n.
将m=-3,n=-代入上式,得原式=-m-6n=-(-3)-6×=5.
23.解:(1)原式=6ab(b2-4a2)
=6ab(b+2a)(b-2a).
(2)原式=2y(x2-4x+4)
=2y(x-2)2.
(3)原式=a2(x-y)-4b2(x-y)
=(x-y)(a2-4b2)
=(x-y)(a+2b)(a-2b).
(4)原式=(2mn+m2+n2)(2mn-m2-n2)=-(m+n)2(m-n)2.
24.解:(x2+px+8)(x2-3x+q)
=x4-3x3+qx2+px3-3px2+pqx+8x2-24x+8q
=x4+(p-3)x3+(q-3p+8)x2+(pq-24)x+8q.
∵展开式中不含x2和x3项,
∴p-3=0,q-3p+8=0,
解得p=3,q=1.
25.解:一定能被20整除.
理由如下:
(n+7)2-(n-3)2=(n+7+n-3)(n+7-n+3)=(2n+4)×10=20(n+2),
∵n为整数,∴n+2为整数.
∴(n+7)2-(n-3)2的值一定能被20整除.
26.解:△ABC是等边三角形.
理由如下:
∵a2+2b2+c2-2b(a+c)=0,
∴a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0.
∴a-b=0,且b-c=0,即a=b=c.
故△ABC是等边三角形.
27.解:(1)绿化面积为(3a+b)(2a+b)-(a+b)2=6a2+5ab+b2-(a2+2ab+b2)=5a2+3ab(平方米).
(2)当a=3,b=2时,5a2+3ab=5×32+3×3×2=45+18=63.
答:绿化面积为(5a2+3ab)平方米,当a=3,b=2时,绿化面积为63平方米.
28.解:(1)①原式=1-26=-63;
②原式=2n+1-2;③原式=x100-1.
(2)①a2-b2;②a3-b3;③a4-b4
一、选择题(每题3分,共30分)
1.计算(a3)2的结果是( )
A.a5 B.-a5 C.a6 D.-a6
2.下列运算正确的是( )
A.3a2-2a2=1 B.a2·a3=a6 C.(ab)2÷a=b2 D.(-ab)3=-a3b3
3.下列式子从左到右变形是因式分解的是( )
A.3x2-3y2-3xy=3(x+y)(x-y)-3xy
B.(y+2x)2-(x+2y)2=3(x+y)(x-y)
C.3(x+y)(x-y)=3x2-3y2
D.(y+2x)2-(x+2y)2=3x2-3y2
4.多项式a(x2-2x+1)与多项式(x-1)(x+1)的公因式是( )
A.x-1 B.x+1 C.x2+1 D.x2
5.下列计算正确的是( )
A.(2a+3b)(3b-2a)=4a2-9b2 B.(-xy2)2÷(-x2y)=-y3
C.=x2-xy+y2 D.-(-a3b2)÷(-a2b2)=a
6.计算××(-1)2 021的结果是( )
A. B. C.1 D.-1
7.若am=2,an=3,ap=5,则a2m+n-p的值是( )
A.2.4 B.2 C.1 D.0
8.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠,无缝隙),则长方形的面积为( )
A.(2a2+5a)cm2 B.(3a+15)cm2
C.(6a+9)cm2 D.(6a+15)cm2
9.已知M=8x2-y2+6x-2,N=9x2+4y+13,则M-N的值( )
A.为正数 B.为负数 C.为非正数 D.不能确定
10.7张如图①的长为a,宽为b(a>b)的小长方形纸片,按图②的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的方式放置,S始终保持不变,则a,b满足( )
A.a=b B.a=3b C.a=b D.a=4b
二、填空题(每题3分,共30分)
11.(-a2)·(a2)2=________.
12.3m=4,3n=6,则3m+2n=________.
13.已知x+y=5,x-y=1,则代数式x2-y2的值是________.
14.计算(1+a)(1-2a)+a(a-2)=________.
15.若|a+2|+a2-4ab+4b2=0,则a=________,b=________.
16.若一个正方形的面积为a2+a+,则此正方形的周长为________.
17.分解因式:m3n-4mn=________________.
18.计算2 021×2 023-2 0222=__________.
19.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成,定义=ad-bc,上述记号就叫做2阶行列式.若=8,则x=________.
20.根据(x-1)(x+1)=x2-1,(x-1)(x2+x+1)=x3-1,(x-1)(x3+x2+x+1)=x4-1,(x-1)(x4+x3+x2+x+1)=x5-1,…的规律,可以得出22 022+22 021+22 020+…+23+22+2+1的末位数字是________.
三、解答题(22,24,25,26题每题6分,21,23题每题8分,27,28题每题10分,共60分)
21.计算:
(1)2a5·(-a)2-(-a2)2·(-7a);
(2)(-a2b2)÷(-ab2)·(-3ab3);
(3)(x-4y)(2x+3y)-(x+2y)(x-y);
(4)[(x+2y)(x-2y)-(2x-y)2+5y2]÷(-2x).
22.先化简,再求值:
(1)(x+5)(x-1)+(x-2)2,其中x=-2;
(2)(m2-6mn+9n2)÷(m-3n)-(4m2-9n2)÷(2m-3n),其中m=-3,n=-.
23.把下列各式分解因式:
(1)6ab3-24a3b; (2)2x2y-8xy+8y;
(3)a2(x-y)+4b2(y-x); (4)4m2n2-(m2+n2)2.
24.已知(x2+px+8)(x2-3x+q)的展开式中不含x2和x3项,求p,q的值.
25.学习了分解因式的知识后,老师提出了这样一个问题:设n为整数,则(n+7)2-(n-3)2的值一定能被20整除吗?若能,请说明理由;若不能,请举出一个反例.
26.已知a,b,c是△ABC的三边长,且a2+2b2+c2-2b(a+c)=0,你能判断△ABC的形状吗?请说明理由.
27.如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间修建一座雕像.
(1)求绿化面积是多少平方米?
(2)求当a=3,b=2时的绿化面积.
28.已知x≠1,(1-x)(1+x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4.
(1)根据以上式子计算:
①(1-2)×(1+2+22+23+24+25);
②2+22+23+…+2n(n为正整数);
③(x-1)(x99+x98+x97+…+x2+x+1).
(2)通过以上计算,请你进行下面的探索:
①(a-b)(a+b)=____________;
②(a-b)(a2+ab+b2)=____________;
③(a-b)(a3+a2b+ab2+b3)=____________.
答案
一、1.C 2.D 3.B 4.A 5.B 6.D
7.A 8.D 9.B 10.B
二、11.-a6 12.144 13.5
14.-a2-3a+1 15.-2;-1
16.4a+2 17.mn(m+2)(m-2)
18.-1 19.2
20.7 解析:由题意可知22 022+22 021+…+22+2+1=(2-1)×(22 022+22 021+…+22+2+1)=22 023-1,而21=2,22=4,23=8,24=16,25=32,26=64,…,可知2n(n为正整数)的末位数字按2,4,8,6的顺序循环,而2 023÷4=505……3,∴22 023的末位数字是8,则22 023-1的末位数字是7.
三、21.解:(1)原式=2a5·a2-a4·(-7a)=2a7+7a5.
(2)原式=a·(-3ab3)=-3a2b3.
(3)原式=2x2+3xy-8xy-12y2-(x2-xy+2xy-2y2)=2x2-5xy-12y2-x2-xy+2y2=x2-6xy-10y2.
(4)原式=[x2-4y2-(4x2-4xy+y2)+5y2]÷(-2x)
=(x2-4y2-4x2+4xy-y2+5y2)÷(-2x)
=(-3x2+4xy)÷(-2x)
=x-2y.
22.解:(1)原式=x2-x+5x-5+x2-4x+4=2x2-1.
当x=-2时,原式=2x2-1=2×(-2)2-1=7.
(2)(m2-6mn+9n2)÷(m-3n)-(4m2-9n2)÷(2m-3n)
=(m-3n)2÷(m-3n)-(2m-3n)(2m+3n)÷(2m-3n)
=m-3n-(2m+3n)
=-m-6n.
将m=-3,n=-代入上式,得原式=-m-6n=-(-3)-6×=5.
23.解:(1)原式=6ab(b2-4a2)
=6ab(b+2a)(b-2a).
(2)原式=2y(x2-4x+4)
=2y(x-2)2.
(3)原式=a2(x-y)-4b2(x-y)
=(x-y)(a2-4b2)
=(x-y)(a+2b)(a-2b).
(4)原式=(2mn+m2+n2)(2mn-m2-n2)=-(m+n)2(m-n)2.
24.解:(x2+px+8)(x2-3x+q)
=x4-3x3+qx2+px3-3px2+pqx+8x2-24x+8q
=x4+(p-3)x3+(q-3p+8)x2+(pq-24)x+8q.
∵展开式中不含x2和x3项,
∴p-3=0,q-3p+8=0,
解得p=3,q=1.
25.解:一定能被20整除.
理由如下:
(n+7)2-(n-3)2=(n+7+n-3)(n+7-n+3)=(2n+4)×10=20(n+2),
∵n为整数,∴n+2为整数.
∴(n+7)2-(n-3)2的值一定能被20整除.
26.解:△ABC是等边三角形.
理由如下:
∵a2+2b2+c2-2b(a+c)=0,
∴a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0.
∴a-b=0,且b-c=0,即a=b=c.
故△ABC是等边三角形.
27.解:(1)绿化面积为(3a+b)(2a+b)-(a+b)2=6a2+5ab+b2-(a2+2ab+b2)=5a2+3ab(平方米).
(2)当a=3,b=2时,5a2+3ab=5×32+3×3×2=45+18=63.
答:绿化面积为(5a2+3ab)平方米,当a=3,b=2时,绿化面积为63平方米.
28.解:(1)①原式=1-26=-63;
②原式=2n+1-2;③原式=x100-1.
(2)①a2-b2;②a3-b3;③a4-b4
