人教B版(2019)高一 必修三7.1.1 角的推广(40张ppt)
文档属性
| 名称 | 人教B版(2019)高一 必修三7.1.1 角的推广(40张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 11.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-03 10:57:51 | ||
图片预览











文档简介
(共40张PPT)
角的推广
高一年级 数学
请同学们观察动画,这些零部件在做什么运动?
旋转运动
平移运动
问题1.用什么度量动画中的机械部
件的旋转运动?
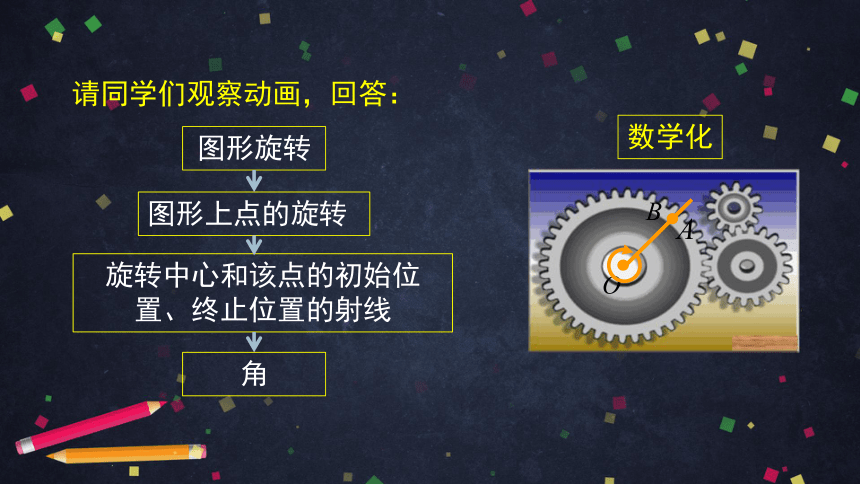
请同学们观察动画,回答:
角
问题2.你对角有哪些认识?
请同学们观察动画,回答:
初中学习过的角:
定义:具有公共端点的两条射线构
成的图形叫作角.
单位:角度制.
范围:
问题3.大齿轮旋转一周,旋转了多
少度?请用数学语言描述
“大齿轮旋转一周”.
请同学们观察动画,回答:
初中学习过的旋转:
在平面内,把一个图形绕点 旋转一个角度,这样的图形变换叫作旋转,点 叫作旋转中心,旋转的角叫作旋转角.
数学化
圆心记为旋转中心 ,在圆上任取一点 ,圆心 与点 构成射线 ,
射线 围绕着点 旋转一周,终点
恰与点 重合,这样我们就得到大齿轮旋转一周是 .
问题4.三个齿轮的旋转有什么区别?
若中号齿轮旋转两周,旋转了
多少度?
请同学们观察动画,回答:
旋转的绝对量,方向.
角的推广
问题5.如何定义角的概念,才能满
足对现实世界中旋转现象的
描述?
请同学们观察动画,回答:
数学化
请同学们观察动画,回答:
图形旋转
图形上点的旋转
旋转中心和该点的初始位置、终止位置的射线
角
角的推广
定义:一条射线绕其端点旋转到另一条射线所形成的图形
称为角,这两条射线分别称为角的始边和终边.
范围:任意角.
分类:按照逆时针方向旋转而成的角称为正角;
按照顺时针方向旋转而成的角称为负角;
当射线没有旋转时称为零角.
问题4. 若中号齿轮旋转两周,旋
转多少度?
请同学们观察动画,回答:
实数
角
正数、零、负数
正角、零角、负角
加减运算:如
平移
正角:逆时针旋转
负角:顺时针旋转
加减运算?旋转的合成?
类比
x
0
1
2
3
-1
-2
-3
问题6.请用数学语言描述绿色齿轮的
旋转运动.
请同学们观察动画,回答:
数学化
第一次旋转所成的角:
第二次旋转所成的角:
两次旋转的角的合成:
多次旋转的角的合成:
角的加法运算
问题7.请用数学语言描述棕色部件的
旋转运动.
请同学们观察动画,回答:
数学化
第一次旋转所成的角:
第二次旋转所成的角:
两次旋转的角的合成:
多次旋转的角的合成:
角的加、减法运算
角的减法运算
滑轨
横杆
滑块
问题8.请用数学语言描述滑块,滑轨,
横杆所做的运动.
请同学们观察动画,回答:
滑轨
横杆
滑块
滑块 相对于滑轨上点 ,在做循环往复的纵向平移运动(上、下平移),滑块 相对于横杆上的点 ,在做横向平移运动(左、右平移).
数学化
滑轨
横杆
滑块
请同学们观察动画,回答:
问题9.如果确定了滑块 的横向、纵向的平移量,是否可以确定滑块 的旋转量呢?(在圆O上的位置?)由此你联想到了什么?
约定:角的顶点与坐标原点重合,角的始边落在x轴
的正半轴上,角的终边上的点可以用坐标(x, y)
来表示.
O
x
y
P
数学化
O
x
y
P
O
x
y
P
O
x
y
P
O
x
y
P
第一象限角
第二象限角
第三象限角
象限角:角的终边在第几象限,就把这个角称为第几象限角.
第四象限角
如果角的终边在坐标轴上,就认为这个角不属于任何象限.
O
x
y
P
O
x
y
P
O
x
y
P
O
x
y
P
终边在x轴正半轴
终边在y轴正半轴
终边在x轴负半轴
终边在y轴负半轴
请在平面直角坐标系中,画出角 和 ,并写出它们所在的象限.
第一象限角
第四象限角
O
x
y
O
x
y
问题10.对于任意给定的一个角,它的终边的位置是否唯一
确定?
给定一个终边位置,它对应的角是否唯一确定?
与 终边相同的角,你还能写出哪些呢?
O
x
y
O
x
y
数形结合
O
x
y
分析:
与 终边相同的角,你还能写出哪些呢?
逆时针
顺时针
与 终边相同的角的集合:
O
x
y
与 终边边相同的角的集合:
从特殊到一般
逆时针
顺时针
数形结合
O
x
y
A
将角α 的终边顺时针方向旋转
得到 的终边;
分析:
例1.如图,已知角α的终边为射线OA,分别作出角
的终边
将角α 的终边逆时针方向旋转
得到 的终边;
例2.写出与角 终边相同的角的集合 ,并把集合 中
满足不等式 的元素 写出来.
解不等式
分析:
例3.写出终边在 x 轴上的角的集合S.
O
x
y
分析:在 内,
终边在 x 轴上的角有两个: 和
,与这两个角终边相同的角
的组成的集合依次为
分析:在 内,终边在 x 轴上的角有两个:
和 ,与这两个角终边相同的角组成的集合依次为
例3.写出终边在 x 轴上的角的集合S.
O
x
y
O
x
y
逆时针
顺时针
逆时针
类比
数形结合
O
x
y
O
x
y
逆时针
顺时针
逆时针
顺时针
类比
数形结合
练习.写出终边在第一象限内的角的集合S.
O
x
y
小结
角
任意角
加减运算
象限角
终边相同的角
推广
旋转
数形 结合
从特殊到一般
数形结合
平面直角
坐标系
实数
类比
作业
1.分别写出与下列各角终边相同的角的集合 ,并把集
合 中满足不等式 的元素写出来.
作业
2.在平面直角坐标系中,集合
中的元素所表示的角的终边在哪些位置?
作业
3.写出终边在第二、第三、第四象限内的角的集合.
感谢观看
角的推广
高一年级 数学
请同学们观察动画,这些零部件在做什么运动?
旋转运动
平移运动
问题1.用什么度量动画中的机械部
件的旋转运动?
请同学们观察动画,回答:
角
问题2.你对角有哪些认识?
请同学们观察动画,回答:
初中学习过的角:
定义:具有公共端点的两条射线构
成的图形叫作角.
单位:角度制.
范围:
问题3.大齿轮旋转一周,旋转了多
少度?请用数学语言描述
“大齿轮旋转一周”.
请同学们观察动画,回答:
初中学习过的旋转:
在平面内,把一个图形绕点 旋转一个角度,这样的图形变换叫作旋转,点 叫作旋转中心,旋转的角叫作旋转角.
数学化
圆心记为旋转中心 ,在圆上任取一点 ,圆心 与点 构成射线 ,
射线 围绕着点 旋转一周,终点
恰与点 重合,这样我们就得到大齿轮旋转一周是 .
问题4.三个齿轮的旋转有什么区别?
若中号齿轮旋转两周,旋转了
多少度?
请同学们观察动画,回答:
旋转的绝对量,方向.
角的推广
问题5.如何定义角的概念,才能满
足对现实世界中旋转现象的
描述?
请同学们观察动画,回答:
数学化
请同学们观察动画,回答:
图形旋转
图形上点的旋转
旋转中心和该点的初始位置、终止位置的射线
角
角的推广
定义:一条射线绕其端点旋转到另一条射线所形成的图形
称为角,这两条射线分别称为角的始边和终边.
范围:任意角.
分类:按照逆时针方向旋转而成的角称为正角;
按照顺时针方向旋转而成的角称为负角;
当射线没有旋转时称为零角.
问题4. 若中号齿轮旋转两周,旋
转多少度?
请同学们观察动画,回答:
实数
角
正数、零、负数
正角、零角、负角
加减运算:如
平移
正角:逆时针旋转
负角:顺时针旋转
加减运算?旋转的合成?
类比
x
0
1
2
3
-1
-2
-3
问题6.请用数学语言描述绿色齿轮的
旋转运动.
请同学们观察动画,回答:
数学化
第一次旋转所成的角:
第二次旋转所成的角:
两次旋转的角的合成:
多次旋转的角的合成:
角的加法运算
问题7.请用数学语言描述棕色部件的
旋转运动.
请同学们观察动画,回答:
数学化
第一次旋转所成的角:
第二次旋转所成的角:
两次旋转的角的合成:
多次旋转的角的合成:
角的加、减法运算
角的减法运算
滑轨
横杆
滑块
问题8.请用数学语言描述滑块,滑轨,
横杆所做的运动.
请同学们观察动画,回答:
滑轨
横杆
滑块
滑块 相对于滑轨上点 ,在做循环往复的纵向平移运动(上、下平移),滑块 相对于横杆上的点 ,在做横向平移运动(左、右平移).
数学化
滑轨
横杆
滑块
请同学们观察动画,回答:
问题9.如果确定了滑块 的横向、纵向的平移量,是否可以确定滑块 的旋转量呢?(在圆O上的位置?)由此你联想到了什么?
约定:角的顶点与坐标原点重合,角的始边落在x轴
的正半轴上,角的终边上的点可以用坐标(x, y)
来表示.
O
x
y
P
数学化
O
x
y
P
O
x
y
P
O
x
y
P
O
x
y
P
第一象限角
第二象限角
第三象限角
象限角:角的终边在第几象限,就把这个角称为第几象限角.
第四象限角
如果角的终边在坐标轴上,就认为这个角不属于任何象限.
O
x
y
P
O
x
y
P
O
x
y
P
O
x
y
P
终边在x轴正半轴
终边在y轴正半轴
终边在x轴负半轴
终边在y轴负半轴
请在平面直角坐标系中,画出角 和 ,并写出它们所在的象限.
第一象限角
第四象限角
O
x
y
O
x
y
问题10.对于任意给定的一个角,它的终边的位置是否唯一
确定?
给定一个终边位置,它对应的角是否唯一确定?
与 终边相同的角,你还能写出哪些呢?
O
x
y
O
x
y
数形结合
O
x
y
分析:
与 终边相同的角,你还能写出哪些呢?
逆时针
顺时针
与 终边相同的角的集合:
O
x
y
与 终边边相同的角的集合:
从特殊到一般
逆时针
顺时针
数形结合
O
x
y
A
将角α 的终边顺时针方向旋转
得到 的终边;
分析:
例1.如图,已知角α的终边为射线OA,分别作出角
的终边
将角α 的终边逆时针方向旋转
得到 的终边;
例2.写出与角 终边相同的角的集合 ,并把集合 中
满足不等式 的元素 写出来.
解不等式
分析:
例3.写出终边在 x 轴上的角的集合S.
O
x
y
分析:在 内,
终边在 x 轴上的角有两个: 和
,与这两个角终边相同的角
的组成的集合依次为
分析:在 内,终边在 x 轴上的角有两个:
和 ,与这两个角终边相同的角组成的集合依次为
例3.写出终边在 x 轴上的角的集合S.
O
x
y
O
x
y
逆时针
顺时针
逆时针
类比
数形结合
O
x
y
O
x
y
逆时针
顺时针
逆时针
顺时针
类比
数形结合
练习.写出终边在第一象限内的角的集合S.
O
x
y
小结
角
任意角
加减运算
象限角
终边相同的角
推广
旋转
数形 结合
从特殊到一般
数形结合
平面直角
坐标系
实数
类比
作业
1.分别写出与下列各角终边相同的角的集合 ,并把集
合 中满足不等式 的元素写出来.
作业
2.在平面直角坐标系中,集合
中的元素所表示的角的终边在哪些位置?
作业
3.写出终边在第二、第三、第四象限内的角的集合.
感谢观看
