华师大版数学八年级上册12.1.3 积的乘方课件(23张ppt)
文档属性
| 名称 | 华师大版数学八年级上册12.1.3 积的乘方课件(23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 17:41:28 | ||
图片预览








文档简介
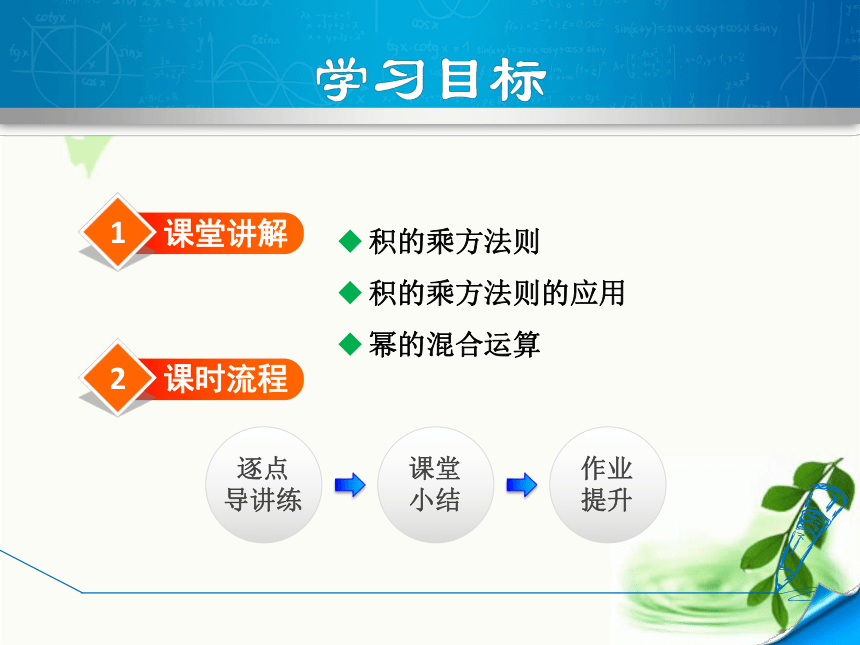
课件23张PPT。第12章 整式的乘除12.1 幂的运算第3课时 积的乘方1课堂讲解积的乘方法则
积的乘方法则的应用
幂的混合运算2课时流程逐点
导讲练课堂小结作业提升1知识点积的乘方法则试一试根据乘方的意义和乘法运算律填空:
(1)(ab)2 = (ab) ? (ab)=(aa) ? (bb)
=a( )b ( );
(2)(ab)3 =_________=_________
=a( )b( ) ;
(3)(ab)4=_________=_________
=a( )b( ) ;知1-导观察这几道题的计算结果,你能发现什么规律?设n为正整数,(ab)n等于什么?概 括知1-导可得
这就是说,积的乘方,把积的每一个
因式分别乘方, 再把所得的幂相乘.(ab)n=anbn(n为正整数).利用这个法则,可直接计算积的乘方.知1-讲?知1-讲 例1 计算:(1) (2b)3; (2) (2a3)2 ;
(3) (-a)3; (4) (-3x)4.
解:(1) (2b)3 = 23b3
= 8b3.
(2)(2a3)2 = 22×(a3)2
= 4a6.
(3)(-a)3 = (-1)3 ? a3
= -a3.
(4)(-3x)4 = (-3)4 ? x4
= 81x4.
知1-讲?知1-讲?知1-讲利用积的乘方法则计 算时,要先确定积中 的因式,然后将每个 因式都乘方,最后求 出所有幂的积.
系数乘方时,要带前 面符号,特别是系数 为-1
时,不要漏掉.
科学记数法形式的 数乘方最后的结果应 该用科
学记数法形式 表示.知1-讲 例3 用简便方法计算:
(1) ×0.254× ×(-4)4;
(2)0.1252 015×(-82 016).
导引:本例如果按照常规方法进行运算,(1)题比较麻烦,
(2)题无法算出结果,因此需采用非常规方法进行计
算.(1)观察该式的特点可知,需利用乘法的交换律
和结合律,并逆用积的乘方法则计算;(2)82 016=
82 015×8,故该式应逆用同底数幂的乘法和积的乘
方法则计算.知1-讲解:(1) ×0.254× ×(-4)4
= ×[0.254×(-4)4]
= ×(0.25×4)4=1×1=1.
(2)0.1252 015×(-82 016)=-0.1252 015×82 016
=-0.1252 015×82 015×8=-(0.125×8)2 015×8
=-12 015×8=-8.知1-讲底数互为倒数的两个幂相乘时,先通过逆用
同底数幂的乘法法则化为幂指数相同的幂,
然后逆用积的乘方法则计算,从而大大简化
运算.?知1-练2知识点积的乘方法则的应用知2-讲积的乘方法则可以逆用,
即anbn=(ab)n(n为正整数).
拓展:(abc)n=anbncn(n为正整数).知2-讲 例4 (1)计算:0.12515×(215)3;
(2)若am=3,bm= ,求(ab)2m的值.
导引:(1)逆用积的乘方法则,可使乘积出现一些简单的数值,
从而使解题简单;(2)直接求字母a,b的值很困难,本题
可以运用幂的运算性质变形,然后整体代入求解.
解:(1)原式= ×(23)15= =1.
(2)因为am=3,bm= ,
所以(ab)2m=[(ab)m]2=(ambm)2=1 如果5n=a,4n=b,那么20n=________.
2 若n为正整数,且x2n=3,则(3x3n)2的值为________.
3 如果(anbm)3=a9b15,那么( )
A.m=3,n=6 B.m=5,n=3
C.m=12,n=3 D.m=9,n=3知2-练知3-讲3知识点幂的混合运算同底数幂的乘法,幂的乘方,积的乘方统称
幂的运算.
易错警示:底数为积的形式,和的形式不能
用,即(a+b)n≠an+bn.知3-讲 例4 计算:(1)(xy2)3;(2)(anb3n)2+(a2b6)n;
(3)[(a2)3+(2a3)2]2.
导引:利用相关的幂的运算法则按先算乘方,再算乘除,最
后算加减,有括号的先算括号里面的顺序进行计算;
有同类项的要合并同类项,使结果最简.
解:(1)原式=x3y6;
(2)原式=a2nb6n+a2nb6n=2a2nb6n;
(3)原式=(a6+4a6)2=(5a6)2=25a12.幂的混合运算顺序与实数的混合运算顺
序相同.知3-讲1 计算(-2a)2-3a2的结果是( )
A.-a2 B.a2
C.-5a2 D.5a2
2 已知2n·xn=22n(n为正整数),求正数x的值. 知3-练1.在进行积的乘方运算时,应把底数的每个因式分
别乘方,不要漏掉任何一项,当底数含有“-”号
时,应将它看成-1,作为一个因式,不要漏乘.
2.三个或三个以上的因式的积的乘方也一样适用:
(abc)n=anbncn(n为正整数),但是要防止出现
(a+b)n=an+bn这样的错误.积的乘方法则也可
以逆用:anbn =(ab)n(n为正整数).完成教材P21T1、2
谢谢!
积的乘方法则的应用
幂的混合运算2课时流程逐点
导讲练课堂小结作业提升1知识点积的乘方法则试一试根据乘方的意义和乘法运算律填空:
(1)(ab)2 = (ab) ? (ab)=(aa) ? (bb)
=a( )b ( );
(2)(ab)3 =_________=_________
=a( )b( ) ;
(3)(ab)4=_________=_________
=a( )b( ) ;知1-导观察这几道题的计算结果,你能发现什么规律?设n为正整数,(ab)n等于什么?概 括知1-导可得
这就是说,积的乘方,把积的每一个
因式分别乘方, 再把所得的幂相乘.(ab)n=anbn(n为正整数).利用这个法则,可直接计算积的乘方.知1-讲?知1-讲 例1 计算:(1) (2b)3; (2) (2a3)2 ;
(3) (-a)3; (4) (-3x)4.
解:(1) (2b)3 = 23b3
= 8b3.
(2)(2a3)2 = 22×(a3)2
= 4a6.
(3)(-a)3 = (-1)3 ? a3
= -a3.
(4)(-3x)4 = (-3)4 ? x4
= 81x4.
知1-讲?知1-讲?知1-讲利用积的乘方法则计 算时,要先确定积中 的因式,然后将每个 因式都乘方,最后求 出所有幂的积.
系数乘方时,要带前 面符号,特别是系数 为-1
时,不要漏掉.
科学记数法形式的 数乘方最后的结果应 该用科
学记数法形式 表示.知1-讲 例3 用简便方法计算:
(1) ×0.254× ×(-4)4;
(2)0.1252 015×(-82 016).
导引:本例如果按照常规方法进行运算,(1)题比较麻烦,
(2)题无法算出结果,因此需采用非常规方法进行计
算.(1)观察该式的特点可知,需利用乘法的交换律
和结合律,并逆用积的乘方法则计算;(2)82 016=
82 015×8,故该式应逆用同底数幂的乘法和积的乘
方法则计算.知1-讲解:(1) ×0.254× ×(-4)4
= ×[0.254×(-4)4]
= ×(0.25×4)4=1×1=1.
(2)0.1252 015×(-82 016)=-0.1252 015×82 016
=-0.1252 015×82 015×8=-(0.125×8)2 015×8
=-12 015×8=-8.知1-讲底数互为倒数的两个幂相乘时,先通过逆用
同底数幂的乘法法则化为幂指数相同的幂,
然后逆用积的乘方法则计算,从而大大简化
运算.?知1-练2知识点积的乘方法则的应用知2-讲积的乘方法则可以逆用,
即anbn=(ab)n(n为正整数).
拓展:(abc)n=anbncn(n为正整数).知2-讲 例4 (1)计算:0.12515×(215)3;
(2)若am=3,bm= ,求(ab)2m的值.
导引:(1)逆用积的乘方法则,可使乘积出现一些简单的数值,
从而使解题简单;(2)直接求字母a,b的值很困难,本题
可以运用幂的运算性质变形,然后整体代入求解.
解:(1)原式= ×(23)15= =1.
(2)因为am=3,bm= ,
所以(ab)2m=[(ab)m]2=(ambm)2=1 如果5n=a,4n=b,那么20n=________.
2 若n为正整数,且x2n=3,则(3x3n)2的值为________.
3 如果(anbm)3=a9b15,那么( )
A.m=3,n=6 B.m=5,n=3
C.m=12,n=3 D.m=9,n=3知2-练知3-讲3知识点幂的混合运算同底数幂的乘法,幂的乘方,积的乘方统称
幂的运算.
易错警示:底数为积的形式,和的形式不能
用,即(a+b)n≠an+bn.知3-讲 例4 计算:(1)(xy2)3;(2)(anb3n)2+(a2b6)n;
(3)[(a2)3+(2a3)2]2.
导引:利用相关的幂的运算法则按先算乘方,再算乘除,最
后算加减,有括号的先算括号里面的顺序进行计算;
有同类项的要合并同类项,使结果最简.
解:(1)原式=x3y6;
(2)原式=a2nb6n+a2nb6n=2a2nb6n;
(3)原式=(a6+4a6)2=(5a6)2=25a12.幂的混合运算顺序与实数的混合运算顺
序相同.知3-讲1 计算(-2a)2-3a2的结果是( )
A.-a2 B.a2
C.-5a2 D.5a2
2 已知2n·xn=22n(n为正整数),求正数x的值. 知3-练1.在进行积的乘方运算时,应把底数的每个因式分
别乘方,不要漏掉任何一项,当底数含有“-”号
时,应将它看成-1,作为一个因式,不要漏乘.
2.三个或三个以上的因式的积的乘方也一样适用:
(abc)n=anbncn(n为正整数),但是要防止出现
(a+b)n=an+bn这样的错误.积的乘方法则也可
以逆用:anbn =(ab)n(n为正整数).完成教材P21T1、2
谢谢!
