华师大版数学八年级上册12.3.1 两数和乘以这两数的差课件(19张ppt)
文档属性
| 名称 | 华师大版数学八年级上册12.3.1 两数和乘以这两数的差课件(19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 816.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 17:49:41 | ||
图片预览





文档简介
课件19张PPT。第12章 整式的乘除12.3 乘法公式第1课时
两数和乘以这两数的差1课堂讲解平方差公式的特征
平方差公式
利用平方差公式简便计算2课时流程逐点
导讲练课堂小结作业提升1知识点平方差公式的特征公式特点:
1. 等号左边是两个二项式相 乘,这两个二项
式中有一 项完全相同,另一项互为 相反数 .
2. 等号右边是乘式中两项的 平方差,即相同
项的平方 减去相反项的平方 .
3. 理解字母a,b的意义,平 方差公式中的a,b既
可代 表一个单项式,也可代表 一个多项式 .知1-讲1 下列计算能运用平方差公式的是( )
A.(m+n)(-m-n) B.(2x+3)(3x-2)
C.(5a2-b2c)(bc2+5a2) D.
2 下列各式中,不能应用平方差公式进行计算的是( )
A.(-2m+n)(-2m-n) B.
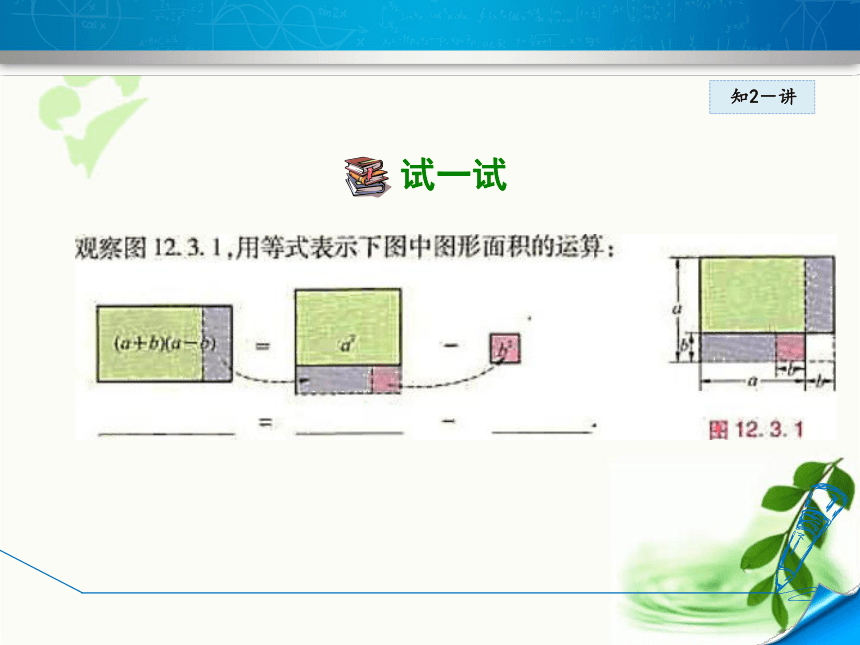
C.(x+2y-1)(x+2y+1) D.(a-b)(-a+b)知1-练2知识点平方差公式知2-导用多项式乘法法则计算:(a+b)(a-b).
(a+b)(a-b)=___________________________.
这两个特殊的多项式相乘,得到的结果特别简洁:
(a + b) (a-b)=a2 -b2.
这就是说,两数和与这两数差的积,等于这两数的平方差.
这个公式叫做两数和与这两数差的乘法公式,有时也简称
为平方差公式.利用这个公式,可以直接计算两数和乘以这两数的差.知2-讲平方差公式:
两数和与这两数差的积,等于这两数的平方差.
用式子表示为:(a+b)(a-b)=a2-b2.
要点精析:(1)在运用公式时,要分清哪个数相当于公式中
的a,哪个数相当于公式中的b,不要混淆.
(2)公式中的a与b可以表示具体的数,也可以表示单项式
或多项式.
(3)平方差公式可以逆用,即a2-b2=(a+b)(a-b).知2-讲例1 计算: (1)(a+3)(a-3); (2)(2a+3b)(2a-3b);
(3)(1+2c)(1-2c); (4)(-2x-y)(2x-y).
解: (1) (a+3)(a-3)=a2-32=a2-9.
(2)(2a+3b)(2a-3b)=(2a)2-(3b)2=4a2-9b2.
(3) (1+2c)(1-2c)=12-(2c)2=1-4c2.
(4)(-2x-y)(2x-y)=(-y-2x)(-y+2x)=(-y)2-(2x)2=y2-4x2.知2-讲 例2 街心花园有一块边长为a米的正方形草坪, 经
统一规划后,南北向增加2米,东西向减少2米.
改造 后得到一块长方形的草坪.求这块长方形
草坪的面积.
解:(a+2)(a-2) = a2- 4.
答:改造后的长方形草坪的面积是(a2-4)平方米.知2-讲1 根据平方差公式填空:
(1)(-3a+2)(-3a-2)=(-3a)2-22=________;
(2)(2x-3)(________)=4x2-9;
(3)(________)(5a+1)=1-25a2.
2 下列运算正确的是( )
A.(a+b)(b-a)=a2-b2
B.(2m+n)(2m-n)=2m2-n2
C.(xm+3)(xm-3)=x2m-9
D.(x-1)(x+1)=(x-1)2知2-练(中考·枣庄)如图,在边长为2a的正方形中央剪去
一边长为(a+2)的小正方形(a>2),将剩余部分沿
虚线剪开密铺成一个平行四边形,则该平行四边
形的面积为( )
A.a2+4 B.2a2+4a
C.3a2-4a-4 D.4a2-a-2知2-练知3-讲3知识点利用平方差公式简便计算例3 计算:1 998 ×2 002.
解:1 998×2 002
=(2 000-2)×(2 000 + 2)
=2 0002-22
=4 000 000 -4
=3 999 996. 例4 计算:(1) 10.3×9.7;
(2) 2 018×2 020-2 0192.
导引:
找出平方差公式的模型,利用平方差公式进行计算.知3-讲解:
(1)10.3×9.7 =(10+0.3)( 10-0.3)=102-0.32
=100-0.09 =99.91.
(2)2 018×2 020-2 0192 =(2 019-1)( 2 019+1)
-2 0192 =2 0192-1-2 0192=-1.知3-讲知3-讲本题运用转化思想求解.运用平方差公式计算两数乘
积问题,关键是找到这两个数的平均数,再将原两个
数与这个平均数进行比较,变形成两数的和与这两数
的差的积的形式,利用平方差公式可求解.知3-练1. 平方差公式的特征:左边是两个二项式相乘,并
且这两个二项式有一项完全相同,另一项互为相
反数;右边是左边的相同项的平方减去互为相反
数的项的平方.
2.公式(a+b)(a-b)=a2-b2中的字母a,b可以是单
项式,也可以是多项式.
3.平方差公式可以逆用:a2-b2=(a+b)(a-b).完成教材P32 T1-3
谢谢!
两数和乘以这两数的差1课堂讲解平方差公式的特征
平方差公式
利用平方差公式简便计算2课时流程逐点
导讲练课堂小结作业提升1知识点平方差公式的特征公式特点:
1. 等号左边是两个二项式相 乘,这两个二项
式中有一 项完全相同,另一项互为 相反数 .
2. 等号右边是乘式中两项的 平方差,即相同
项的平方 减去相反项的平方 .
3. 理解字母a,b的意义,平 方差公式中的a,b既
可代 表一个单项式,也可代表 一个多项式 .知1-讲1 下列计算能运用平方差公式的是( )
A.(m+n)(-m-n) B.(2x+3)(3x-2)
C.(5a2-b2c)(bc2+5a2) D.
2 下列各式中,不能应用平方差公式进行计算的是( )
A.(-2m+n)(-2m-n) B.
C.(x+2y-1)(x+2y+1) D.(a-b)(-a+b)知1-练2知识点平方差公式知2-导用多项式乘法法则计算:(a+b)(a-b).
(a+b)(a-b)=___________________________.
这两个特殊的多项式相乘,得到的结果特别简洁:
(a + b) (a-b)=a2 -b2.
这就是说,两数和与这两数差的积,等于这两数的平方差.
这个公式叫做两数和与这两数差的乘法公式,有时也简称
为平方差公式.利用这个公式,可以直接计算两数和乘以这两数的差.知2-讲平方差公式:
两数和与这两数差的积,等于这两数的平方差.
用式子表示为:(a+b)(a-b)=a2-b2.
要点精析:(1)在运用公式时,要分清哪个数相当于公式中
的a,哪个数相当于公式中的b,不要混淆.
(2)公式中的a与b可以表示具体的数,也可以表示单项式
或多项式.
(3)平方差公式可以逆用,即a2-b2=(a+b)(a-b).知2-讲例1 计算: (1)(a+3)(a-3); (2)(2a+3b)(2a-3b);
(3)(1+2c)(1-2c); (4)(-2x-y)(2x-y).
解: (1) (a+3)(a-3)=a2-32=a2-9.
(2)(2a+3b)(2a-3b)=(2a)2-(3b)2=4a2-9b2.
(3) (1+2c)(1-2c)=12-(2c)2=1-4c2.
(4)(-2x-y)(2x-y)=(-y-2x)(-y+2x)=(-y)2-(2x)2=y2-4x2.知2-讲 例2 街心花园有一块边长为a米的正方形草坪, 经
统一规划后,南北向增加2米,东西向减少2米.
改造 后得到一块长方形的草坪.求这块长方形
草坪的面积.
解:(a+2)(a-2) = a2- 4.
答:改造后的长方形草坪的面积是(a2-4)平方米.知2-讲1 根据平方差公式填空:
(1)(-3a+2)(-3a-2)=(-3a)2-22=________;
(2)(2x-3)(________)=4x2-9;
(3)(________)(5a+1)=1-25a2.
2 下列运算正确的是( )
A.(a+b)(b-a)=a2-b2
B.(2m+n)(2m-n)=2m2-n2
C.(xm+3)(xm-3)=x2m-9
D.(x-1)(x+1)=(x-1)2知2-练(中考·枣庄)如图,在边长为2a的正方形中央剪去
一边长为(a+2)的小正方形(a>2),将剩余部分沿
虚线剪开密铺成一个平行四边形,则该平行四边
形的面积为( )
A.a2+4 B.2a2+4a
C.3a2-4a-4 D.4a2-a-2知2-练知3-讲3知识点利用平方差公式简便计算例3 计算:1 998 ×2 002.
解:1 998×2 002
=(2 000-2)×(2 000 + 2)
=2 0002-22
=4 000 000 -4
=3 999 996. 例4 计算:(1) 10.3×9.7;
(2) 2 018×2 020-2 0192.
导引:
找出平方差公式的模型,利用平方差公式进行计算.知3-讲解:
(1)10.3×9.7 =(10+0.3)( 10-0.3)=102-0.32
=100-0.09 =99.91.
(2)2 018×2 020-2 0192 =(2 019-1)( 2 019+1)
-2 0192 =2 0192-1-2 0192=-1.知3-讲知3-讲本题运用转化思想求解.运用平方差公式计算两数乘
积问题,关键是找到这两个数的平均数,再将原两个
数与这个平均数进行比较,变形成两数的和与这两数
的差的积的形式,利用平方差公式可求解.知3-练1. 平方差公式的特征:左边是两个二项式相乘,并
且这两个二项式有一项完全相同,另一项互为相
反数;右边是左边的相同项的平方减去互为相反
数的项的平方.
2.公式(a+b)(a-b)=a2-b2中的字母a,b可以是单
项式,也可以是多项式.
3.平方差公式可以逆用:a2-b2=(a+b)(a-b).完成教材P32 T1-3
谢谢!
