华师大版数学八年级上册12.3.2 两数和(差)的平方 课件(23张ppt)
文档属性
| 名称 | 华师大版数学八年级上册12.3.2 两数和(差)的平方 课件(23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 17:55:41 | ||
图片预览







文档简介
课件23张PPT。第12章 整式的乘除12.3 乘法公式第2课时
两数和(差)的平方 1课堂讲解完全平方公式的特征
完全平方公式
完全平方公式的应用 2课时流程逐点
导讲练课堂小结作业提升1知识点完全平方公式的特征弄清公式的特征
公式的左边是一个二项式的完全平方,公式的
右边是一个三项式,包括左边二项式的各项的
平方和,另一项是这两项的乘积的2倍.知1-讲1 若x2+6x+k是完全平方式,则k等于( )
A.9 B.-9 C.±9 D.±3
小明计算一个二项式的平方时,得到正确结果a2-10ab+
■,但最后一项不慎被污染了,这一项应是( )
A.5b B.5b2 C.25b2 D.100b2
3 下列变形中,错误的是( )
①(b-4c)2=b2-16c2; ②(a-2bc)2=a2+4abc+4b2c2;
③(x+y)2=x2+xy+y2;
④(4m-n)2=16m2-8mn+n2.
A.①②③ B.①②④ C.①③④ D.②③④知1-练2知识点完全平方公式知2-导利用这个公式,可以直接计算两数和的平方.用多项式乘法法则计算:(a+b)2.
(a+b)2=(a+b)(a+b)=____________________.
我们又得到一个漂亮的结果:
(a + b)2 =a2 +2ab+b2.
这就是说,两数和的平方,等于这两数的平 方和加上它们
的积的2倍.
这个公式叫做两数和的平方公式.知2-讲两数和(差)的平方公式(也称完全平方公式):
两数和(或差)的平方,等于这两数的平方和加上(减去)它
们的积的2倍.
用式子表示为:(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
要点精析:(1)理解字母a,b的意义:公式中的字母a,b可以
表示具体的数,也可以表示单项式或多项式.
(2)学会用口诀加深记忆:对于公式(a±b)2=a2±2ab+b2,可
以用下面简单的口诀来记忆:头平方和尾平方,头(乘)尾两
倍在中央,中间符号照原样.知2-讲例1 计算:(1)(2x+3y)2;(2)(2a+ )2.
解:(1)(2x+3y)2=(2x)2 +2 ? 2x ? 3y + (3y)2 =4x2+12xy+9y2.
(2)(2a+ )2=(2a)2 + 2 ? 2a ? +
=4a2 + 2ab +知2-讲知2-讲推导两数差的平方公式.
我们可以根据多项式的乘法法则直接计算(a-b)2. 注意到a-b =
a+(-b),也可以利用两数和的平方公式 来计算,即
(a-b)2 =[a+(-b) ]2 =a2+2a(-b)+(-b)2 =a2-2ab+b2.
这样就得到了两数差的平方公式:
(a-b)2=a2-2ab+b2.
这就是说,两数差的平方,等于这两数的平方和减去 它们的
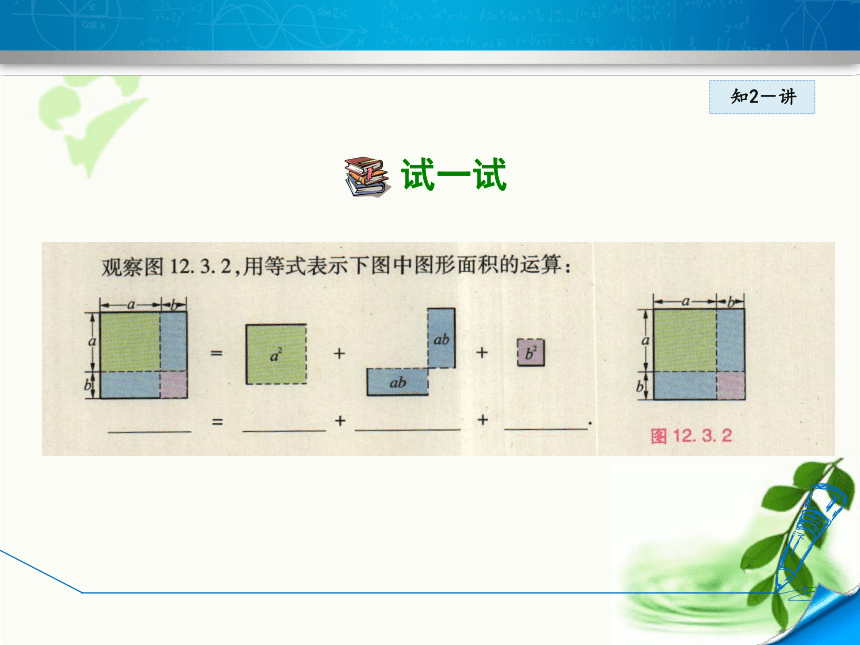
积的2倍.知2-讲你能用图 12.3.3中的面积 关系来解释两数 差的平方公式吗?
例2 计算:(1) (3x-2y)2;(2)
解:(1)(3x-2y)2=(3x)2 - 2 ? 3x ? 2y + (2y)2 =9x2 -12xy+ 4y2.知2-讲知2-讲在应用公式(a±b)2=a2±2ab+b2时关键是弄清题目
中哪一个相当于公式中的a,哪一个相当于公式中的
b,同时还要确定用两数和的平方公式还是两数差的
平方公式.1 计算(-a-b)2等于( )
A.a2+b2 B.a2-b2
C.a2+2ab+b2 D.a2-2ab+b2
2 (中考·遵义)下列运算正确的是( )
A.4a-a=3 B.2(2a-b)=4a-b
C.(a+b)2=a2+b2 D.(a+2)(a-2)=a2-4知2-练知3-讲3知识点完全平方公式的应用拓展:
两数和(差)的平方公式的几种常见变形公式: (1)a2+b2=(a+b)2-2ab=(a-b)2+2ab;
(2)(a+b)2-(a-b)2=4ab;
(3)(a-b)2 =(a+b)2-4ab;
(4)(a+b)2 +(a-b)2 = 2(a2+b2); 知3-讲? 例3 (1)若(x-5)2=x2+kx+25,则k的值是多少?
(2)先化简,再求值:(1+a)(1-a)+(a-2)2,
其中a=-3.
(3)已知x2-4x+1=0,求代数式(2x-3)2-(x+y)
(x-y)-y2的值.
导引:对于(1),把等号左边的式子展开后对比各项,即可
得解;对于(2),利用平方差公式和两数和(差)的平
方公式展开,合并同类项后代入求值;对于(3),
先化简代数式,再将条件变形整体代入求值.知3-讲解:(1)依题意,得x2-10x+25=x2+kx+25.
所以k=-10.
(2)原式=1-a2+a2-4a+4=-4a+5,
当a=-3时,原式=-4×(-3)+5=12+5=17.
(3)原式=4x2-12x+9-x2+y2-y2=3x2-12x+9
=3(x2-4x+3).
因为x2-4x+1=0,所以x2-4x=-1,
所以,原式=3×(-1+3)=3×2=6.知3-讲 例4 已知a2+b2=13,ab=6,
求(a+b)2,(a-b)2的值.
导引:利用两数和(差)的平方公式展开,得到两数的平方
和与这两数积的两倍,再将条件代入求解.
解:因为a2+b2=13,ab=6,
所以(a+b)2=a2+b2+2ab=13+2×6=25,
(a-b)2=a2+b2-2ab=13-2×6=1.知3-讲知3-讲在利用两数和(差)的平方公式进行计算时,经常会遇
到这个公式的如下变形:①(a+b)2-2ab=a2+b2;
②(a-b)2+2ab=a2+b2;③(a+b)2+(a-b)2=2(a2+
b2);④(a+b)2-(a-b)2=4ab,
灵活运用这些公式的变形,往往可以解答一些特殊的
计算问题,培养综合运用知识的能力.知3-练1 若(a+b)2=(a-b)2+A,则A为( )
A.2ab B.-2ab C.4ab D.-4ab
2 若(x+3)2=x2+ax+9,则a的值为( )
A.3 B.±3 C.6 D.±6
(2015·邵阳)已知a+b=3,ab=2,则a2+b2的值
为( )
A.3 B.4 C.5 D.61.完全平方公式的特征:左边是二项式的平方,右边是二次三项式,
其中两项分别是公式左边两项的平方,中间一项是左边二项式中
两项乘积的2倍.
2.公式中的a,b可以是单项式,也可以是多项式.公式也可以逆用:
a2±2ab+b2=(a±b)2.
3.利用完全平方公式化简求值时常利用整体思想,把a2+b2 ,ab,
a±b看成一个整体,利用完全平方公式的变形,整体代换求值,
常见的变形公式有:(1)a2+b2=(a+b)2-2ab=(a-b)2+2ab;
(2) (a+b)2-(a-b)2=4ab.
完成教材P35 T1-3
谢谢!
两数和(差)的平方 1课堂讲解完全平方公式的特征
完全平方公式
完全平方公式的应用 2课时流程逐点
导讲练课堂小结作业提升1知识点完全平方公式的特征弄清公式的特征
公式的左边是一个二项式的完全平方,公式的
右边是一个三项式,包括左边二项式的各项的
平方和,另一项是这两项的乘积的2倍.知1-讲1 若x2+6x+k是完全平方式,则k等于( )
A.9 B.-9 C.±9 D.±3
小明计算一个二项式的平方时,得到正确结果a2-10ab+
■,但最后一项不慎被污染了,这一项应是( )
A.5b B.5b2 C.25b2 D.100b2
3 下列变形中,错误的是( )
①(b-4c)2=b2-16c2; ②(a-2bc)2=a2+4abc+4b2c2;
③(x+y)2=x2+xy+y2;
④(4m-n)2=16m2-8mn+n2.
A.①②③ B.①②④ C.①③④ D.②③④知1-练2知识点完全平方公式知2-导利用这个公式,可以直接计算两数和的平方.用多项式乘法法则计算:(a+b)2.
(a+b)2=(a+b)(a+b)=____________________.
我们又得到一个漂亮的结果:
(a + b)2 =a2 +2ab+b2.
这就是说,两数和的平方,等于这两数的平 方和加上它们
的积的2倍.
这个公式叫做两数和的平方公式.知2-讲两数和(差)的平方公式(也称完全平方公式):
两数和(或差)的平方,等于这两数的平方和加上(减去)它
们的积的2倍.
用式子表示为:(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
要点精析:(1)理解字母a,b的意义:公式中的字母a,b可以
表示具体的数,也可以表示单项式或多项式.
(2)学会用口诀加深记忆:对于公式(a±b)2=a2±2ab+b2,可
以用下面简单的口诀来记忆:头平方和尾平方,头(乘)尾两
倍在中央,中间符号照原样.知2-讲例1 计算:(1)(2x+3y)2;(2)(2a+ )2.
解:(1)(2x+3y)2=(2x)2 +2 ? 2x ? 3y + (3y)2 =4x2+12xy+9y2.
(2)(2a+ )2=(2a)2 + 2 ? 2a ? +
=4a2 + 2ab +知2-讲知2-讲推导两数差的平方公式.
我们可以根据多项式的乘法法则直接计算(a-b)2. 注意到a-b =
a+(-b),也可以利用两数和的平方公式 来计算,即
(a-b)2 =[a+(-b) ]2 =a2+2a(-b)+(-b)2 =a2-2ab+b2.
这样就得到了两数差的平方公式:
(a-b)2=a2-2ab+b2.
这就是说,两数差的平方,等于这两数的平方和减去 它们的
积的2倍.知2-讲你能用图 12.3.3中的面积 关系来解释两数 差的平方公式吗?
例2 计算:(1) (3x-2y)2;(2)
解:(1)(3x-2y)2=(3x)2 - 2 ? 3x ? 2y + (2y)2 =9x2 -12xy+ 4y2.知2-讲知2-讲在应用公式(a±b)2=a2±2ab+b2时关键是弄清题目
中哪一个相当于公式中的a,哪一个相当于公式中的
b,同时还要确定用两数和的平方公式还是两数差的
平方公式.1 计算(-a-b)2等于( )
A.a2+b2 B.a2-b2
C.a2+2ab+b2 D.a2-2ab+b2
2 (中考·遵义)下列运算正确的是( )
A.4a-a=3 B.2(2a-b)=4a-b
C.(a+b)2=a2+b2 D.(a+2)(a-2)=a2-4知2-练知3-讲3知识点完全平方公式的应用拓展:
两数和(差)的平方公式的几种常见变形公式: (1)a2+b2=(a+b)2-2ab=(a-b)2+2ab;
(2)(a+b)2-(a-b)2=4ab;
(3)(a-b)2 =(a+b)2-4ab;
(4)(a+b)2 +(a-b)2 = 2(a2+b2); 知3-讲? 例3 (1)若(x-5)2=x2+kx+25,则k的值是多少?
(2)先化简,再求值:(1+a)(1-a)+(a-2)2,
其中a=-3.
(3)已知x2-4x+1=0,求代数式(2x-3)2-(x+y)
(x-y)-y2的值.
导引:对于(1),把等号左边的式子展开后对比各项,即可
得解;对于(2),利用平方差公式和两数和(差)的平
方公式展开,合并同类项后代入求值;对于(3),
先化简代数式,再将条件变形整体代入求值.知3-讲解:(1)依题意,得x2-10x+25=x2+kx+25.
所以k=-10.
(2)原式=1-a2+a2-4a+4=-4a+5,
当a=-3时,原式=-4×(-3)+5=12+5=17.
(3)原式=4x2-12x+9-x2+y2-y2=3x2-12x+9
=3(x2-4x+3).
因为x2-4x+1=0,所以x2-4x=-1,
所以,原式=3×(-1+3)=3×2=6.知3-讲 例4 已知a2+b2=13,ab=6,
求(a+b)2,(a-b)2的值.
导引:利用两数和(差)的平方公式展开,得到两数的平方
和与这两数积的两倍,再将条件代入求解.
解:因为a2+b2=13,ab=6,
所以(a+b)2=a2+b2+2ab=13+2×6=25,
(a-b)2=a2+b2-2ab=13-2×6=1.知3-讲知3-讲在利用两数和(差)的平方公式进行计算时,经常会遇
到这个公式的如下变形:①(a+b)2-2ab=a2+b2;
②(a-b)2+2ab=a2+b2;③(a+b)2+(a-b)2=2(a2+
b2);④(a+b)2-(a-b)2=4ab,
灵活运用这些公式的变形,往往可以解答一些特殊的
计算问题,培养综合运用知识的能力.知3-练1 若(a+b)2=(a-b)2+A,则A为( )
A.2ab B.-2ab C.4ab D.-4ab
2 若(x+3)2=x2+ax+9,则a的值为( )
A.3 B.±3 C.6 D.±6
(2015·邵阳)已知a+b=3,ab=2,则a2+b2的值
为( )
A.3 B.4 C.5 D.61.完全平方公式的特征:左边是二项式的平方,右边是二次三项式,
其中两项分别是公式左边两项的平方,中间一项是左边二项式中
两项乘积的2倍.
2.公式中的a,b可以是单项式,也可以是多项式.公式也可以逆用:
a2±2ab+b2=(a±b)2.
3.利用完全平方公式化简求值时常利用整体思想,把a2+b2 ,ab,
a±b看成一个整体,利用完全平方公式的变形,整体代换求值,
常见的变形公式有:(1)a2+b2=(a+b)2-2ab=(a-b)2+2ab;
(2) (a+b)2-(a-b)2=4ab.
完成教材P35 T1-3
谢谢!
