初中数学中考专区二轮专题---K型题(pdf版含答案)
文档属性
| 名称 | 初中数学中考专区二轮专题---K型题(pdf版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 335.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 00:00:00 | ||
图片预览


文档简介
微知识:利用“K”型相似解决问题
“K”型相似,是说具有像英文字母 k 的形状的图形,因在构成中形成特殊的
角------直角。在计算和证明中能利用性质:同角的余角相等,进行找到相等的
角,从而证明两个三角形全等或相似。因为 k具有固定性,所以称为“K”型相
似,也有资料称“一线三直角”。
为能更好的认识“K”型相似我们来看下面的例题:
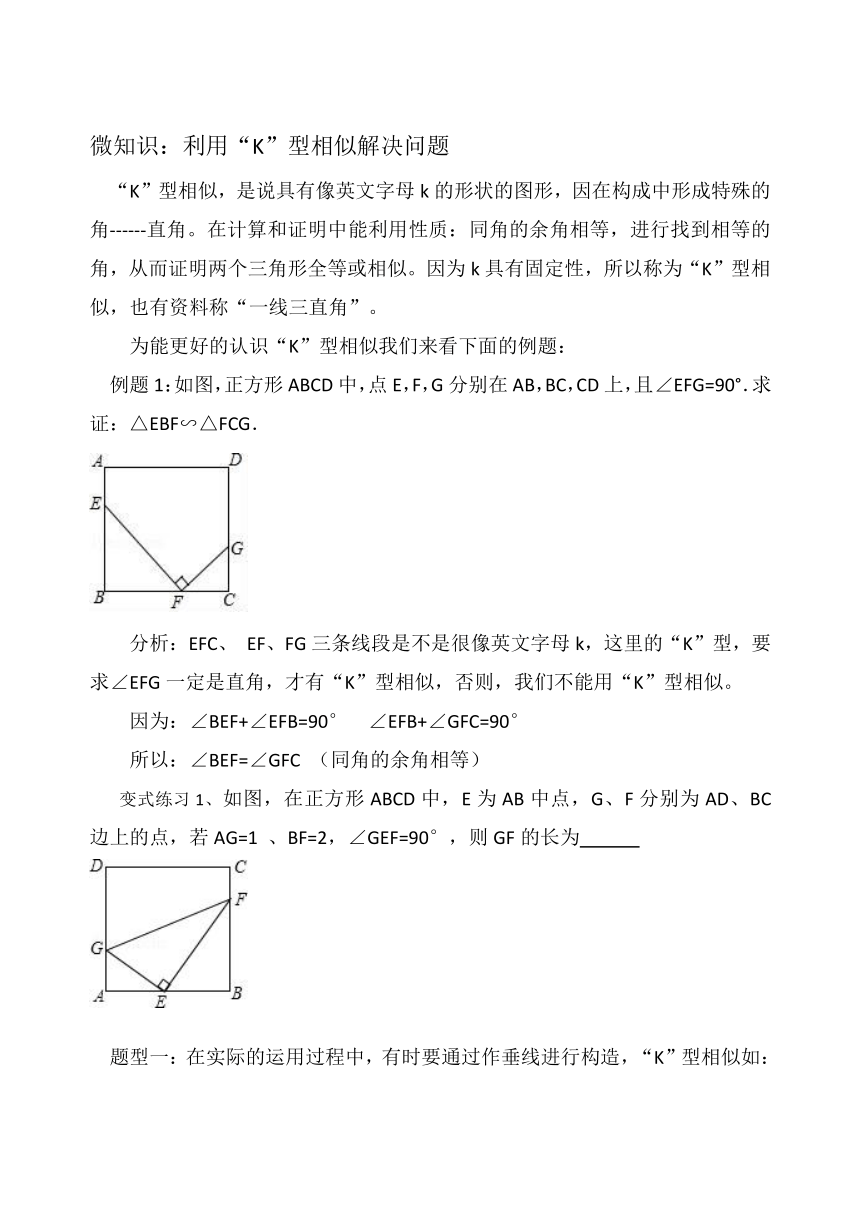
例题 1:如图,正方形 ABCD中,点 E,F,G分别在 AB,BC,CD上,且∠EFG=90°.求
证:△EBF∽△FCG.
分析:EFC、 EF、FG三条线段是不是很像英文字母 k,这里的“K”型,要
求∠EFG 一定是直角,才有“K”型相似,否则,我们不能用“K”型相似。
因为:∠BEF+∠EFB=90° ∠EFB+∠GFC=90°
所以:∠BEF=∠GFC (同角的余角相等)
变式练习 1、如图,在正方形 ABCD 中,E 为 AB 中点,G、F 分别为 AD、BC
边上的点,若 AG=1 、BF=2,∠GEF=90°,则 GF 的长为
题型一:在实际的运用过程中,有时要通过作垂线进行构造,“K”型相似如:
例题 2、如图,将正方形 OABC 放在平面直角坐标系中,O 是原点,A 的坐
标为(1, ),则点 C 的坐标为
分析:要分别过 A、C 分别作 AM⊥X 轴、CN⊥X 轴交 X 轴于点 M、N,构
造出需要的图形。
变式练习 2、如图,正方形 ABCD 中,M 为 BC 上一点,ME AM? ,ME交
AD的延长线于点 E.若 AB=12,BM=5,则 DE的长为
变式练习 3、如图,在边长 10cm 为的正方形 ABCD 中,P 为 AB 边上任意一
点(P 不与 A、B两点重合),连结 DP,过点 P 作 PE⊥DP,垂足为 P,交 BC 于
点 E,则 BE 的最大长度为
题型二:平面直角坐标系中利用“K”型相似求值:
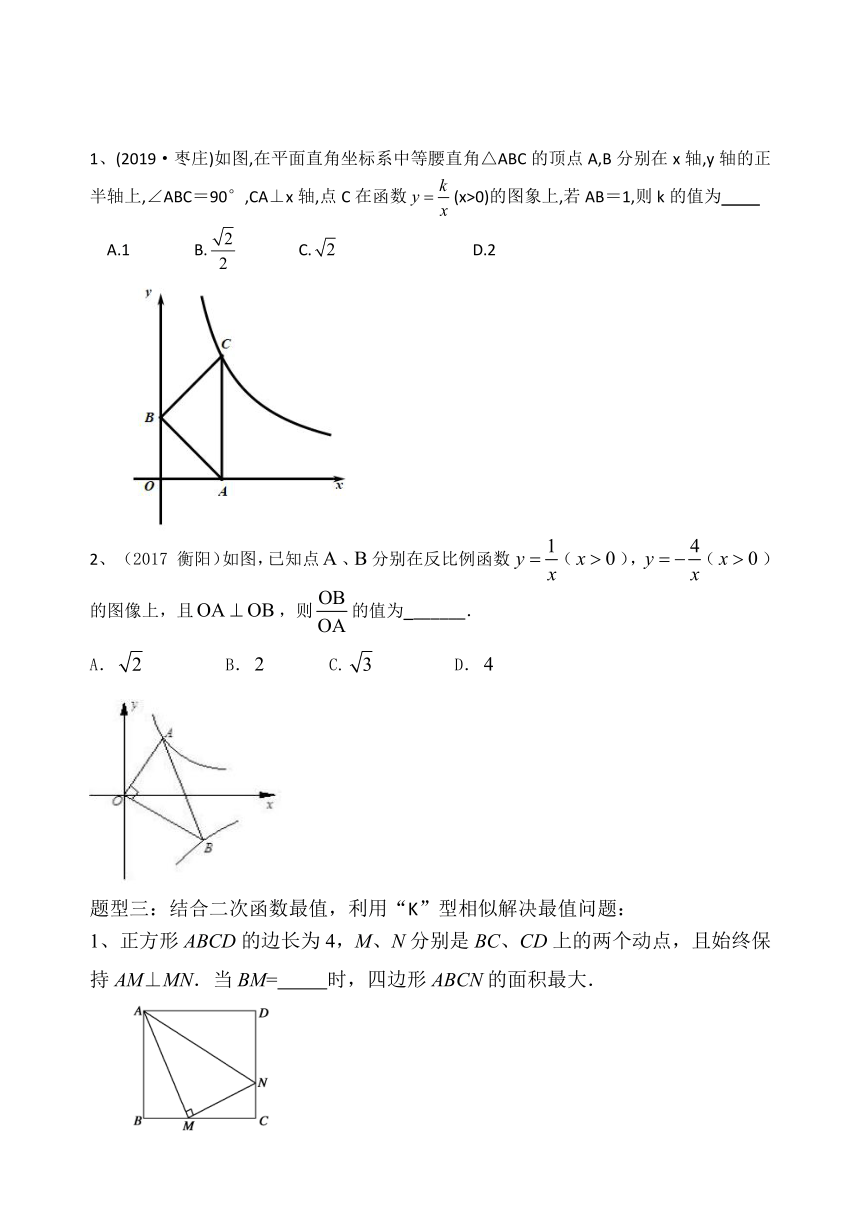
1、(2019·枣庄)如图,在平面直角坐标系中等腰直角△ABC 的顶点 A,B 分别在 x 轴,y 轴的正
半轴上,∠ABC=90°,CA⊥x 轴,点 C 在函数
ky
x
? (x>0)的图象上,若 AB=1,则 k 的值为
A.1 B.
2
2
C. 2 D.2
2、(2017 衡阳)如图,已知点?、?分别在反比例函数
1y
x
? ( 0x ? ), 4y
x
? ? ( 0x ? )
的图像上,且?? ? ??,则
??
??
的值为_______.
A. 2 B. 2 C. 3 D. 4
题型三:结合二次函数最值,利用“K”型相似解决最值问题:
1、正方形 ABCD的边长为 4,M、N分别是 BC、CD上的两个动点,且始终保
持 AM⊥MN.当 BM= 时,四边形 ABCN的面积最大.
2、如图,正方形 ABCD的边长为 4,E、F分别是 BC、CD上的两个动点,且
AE⊥EF.则 AF的最小值是 .
中考在线:
1、如图,已知矩形 ABCD中,E是 AD上的一点,F是 AB上的一点,EF⊥EC,
且 EF=EC,DE=4cm,矩形 ABCD的周长为 32cm,则 AE的长为 .
2、(2017 常州) 如图,已知矩形 ABCD的顶点 ,A D分别落在 x轴、 y轴上,
2 6, : 3 :1OD OA AD AB? ? ? ,则点C的坐标是_______.
3、如图,在函数 )0(11 <xx
ky ? 和 )0(
x
k
y 22 >x? 的图象上,分别有 A、B 两点,若 AB
∥x 轴,交 y 轴于点 C,且 OA⊥OB,S△AOC= 2
1
,S△BOC= 2
9
,则线段 AB 的长度=_______
4、 (2019·潍坊)如图,Rt△AOB 中,∠AOB=90°,顶点 A,B 分别在反比例
函数
1 ( 0)y x
x
? ? 与
5 ( 0)y x
x
?
? ? 的图象上.则 tan∠BAO的值为 .
5.(2018?聊城)如图,在平面直角坐标系中,矩形 OABC 的两边 OA,OC 分
别在 x 轴和 y 轴上,并且 OA=5,OC=3.若把矩形 OABC 绕着点 O 逆时针旋转,
使点 A恰好落在 BC 边上的 A1处,则点 C的对应点 C1的坐标为_______.
A.(﹣ , ) B.(﹣ , ) C.(﹣ , ) D.(﹣ , )
6、(2018?达州)如图,平面直角坐标系中,矩形 OABC 的顶点 A(﹣6,0),
C(0,2 ).将矩形 OABC 绕点 O 顺时针方向旋转,使点 A 恰好落在 OB 上的
点 A1处,则点 B的对应点 B1的坐标为 .
7、如图,四边形 OABC 是矩形,点 A 的坐标为(8,0) ,点 C的坐标为
(0,4),把矩形 OABC 沿 OB 折叠,点 C落在点 D 处,则点 D的坐标为________.
8、如图,把正方形纸片 ABCD 沿对边中点所在的直线对折后展开,折痕为 MN,
再过点 B 折叠纸片,使点 A落在 MN上的点 F 处,折痕为 BE.若 AB 的长为 2,
则 EN的长为_______.
8、(2019年十堰)如图,平面直角坐标系中,A(﹣8,0),B(﹣8,4),C(0,4),
反比例函数 y=k
x
的图象分别与线段 AB,BC交于点 D,E,连接 DE.若点 B关于 DE的对
称点恰好在 OA上,则 k=
参考答案:
例题 1:见分析 变式练习 1、3
题型一:例题 2、(﹣ ,1)
变式练习 2、
5
109
变式练习 3、
2
5
题型二:1、A 2、B
题型三:1、2 2、5
中考在线:1、6 2、(2,7) 3、
4、
5 5、A.
6、
(﹣2 ,6)
7、 8、 3-32 9、﹣12
“K”型相似,是说具有像英文字母 k 的形状的图形,因在构成中形成特殊的
角------直角。在计算和证明中能利用性质:同角的余角相等,进行找到相等的
角,从而证明两个三角形全等或相似。因为 k具有固定性,所以称为“K”型相
似,也有资料称“一线三直角”。
为能更好的认识“K”型相似我们来看下面的例题:
例题 1:如图,正方形 ABCD中,点 E,F,G分别在 AB,BC,CD上,且∠EFG=90°.求
证:△EBF∽△FCG.
分析:EFC、 EF、FG三条线段是不是很像英文字母 k,这里的“K”型,要
求∠EFG 一定是直角,才有“K”型相似,否则,我们不能用“K”型相似。
因为:∠BEF+∠EFB=90° ∠EFB+∠GFC=90°
所以:∠BEF=∠GFC (同角的余角相等)
变式练习 1、如图,在正方形 ABCD 中,E 为 AB 中点,G、F 分别为 AD、BC
边上的点,若 AG=1 、BF=2,∠GEF=90°,则 GF 的长为
题型一:在实际的运用过程中,有时要通过作垂线进行构造,“K”型相似如:
例题 2、如图,将正方形 OABC 放在平面直角坐标系中,O 是原点,A 的坐
标为(1, ),则点 C 的坐标为
分析:要分别过 A、C 分别作 AM⊥X 轴、CN⊥X 轴交 X 轴于点 M、N,构
造出需要的图形。
变式练习 2、如图,正方形 ABCD 中,M 为 BC 上一点,ME AM? ,ME交
AD的延长线于点 E.若 AB=12,BM=5,则 DE的长为
变式练习 3、如图,在边长 10cm 为的正方形 ABCD 中,P 为 AB 边上任意一
点(P 不与 A、B两点重合),连结 DP,过点 P 作 PE⊥DP,垂足为 P,交 BC 于
点 E,则 BE 的最大长度为
题型二:平面直角坐标系中利用“K”型相似求值:
1、(2019·枣庄)如图,在平面直角坐标系中等腰直角△ABC 的顶点 A,B 分别在 x 轴,y 轴的正
半轴上,∠ABC=90°,CA⊥x 轴,点 C 在函数
ky
x
? (x>0)的图象上,若 AB=1,则 k 的值为
A.1 B.
2
2
C. 2 D.2
2、(2017 衡阳)如图,已知点?、?分别在反比例函数
1y
x
? ( 0x ? ), 4y
x
? ? ( 0x ? )
的图像上,且?? ? ??,则
??
??
的值为_______.
A. 2 B. 2 C. 3 D. 4
题型三:结合二次函数最值,利用“K”型相似解决最值问题:
1、正方形 ABCD的边长为 4,M、N分别是 BC、CD上的两个动点,且始终保
持 AM⊥MN.当 BM= 时,四边形 ABCN的面积最大.
2、如图,正方形 ABCD的边长为 4,E、F分别是 BC、CD上的两个动点,且
AE⊥EF.则 AF的最小值是 .
中考在线:
1、如图,已知矩形 ABCD中,E是 AD上的一点,F是 AB上的一点,EF⊥EC,
且 EF=EC,DE=4cm,矩形 ABCD的周长为 32cm,则 AE的长为 .
2、(2017 常州) 如图,已知矩形 ABCD的顶点 ,A D分别落在 x轴、 y轴上,
2 6, : 3 :1OD OA AD AB? ? ? ,则点C的坐标是_______.
3、如图,在函数 )0(11 <xx
ky ? 和 )0(
x
k
y 22 >x? 的图象上,分别有 A、B 两点,若 AB
∥x 轴,交 y 轴于点 C,且 OA⊥OB,S△AOC= 2
1
,S△BOC= 2
9
,则线段 AB 的长度=_______
4、 (2019·潍坊)如图,Rt△AOB 中,∠AOB=90°,顶点 A,B 分别在反比例
函数
1 ( 0)y x
x
? ? 与
5 ( 0)y x
x
?
? ? 的图象上.则 tan∠BAO的值为 .
5.(2018?聊城)如图,在平面直角坐标系中,矩形 OABC 的两边 OA,OC 分
别在 x 轴和 y 轴上,并且 OA=5,OC=3.若把矩形 OABC 绕着点 O 逆时针旋转,
使点 A恰好落在 BC 边上的 A1处,则点 C的对应点 C1的坐标为_______.
A.(﹣ , ) B.(﹣ , ) C.(﹣ , ) D.(﹣ , )
6、(2018?达州)如图,平面直角坐标系中,矩形 OABC 的顶点 A(﹣6,0),
C(0,2 ).将矩形 OABC 绕点 O 顺时针方向旋转,使点 A 恰好落在 OB 上的
点 A1处,则点 B的对应点 B1的坐标为 .
7、如图,四边形 OABC 是矩形,点 A 的坐标为(8,0) ,点 C的坐标为
(0,4),把矩形 OABC 沿 OB 折叠,点 C落在点 D 处,则点 D的坐标为________.
8、如图,把正方形纸片 ABCD 沿对边中点所在的直线对折后展开,折痕为 MN,
再过点 B 折叠纸片,使点 A落在 MN上的点 F 处,折痕为 BE.若 AB 的长为 2,
则 EN的长为_______.
8、(2019年十堰)如图,平面直角坐标系中,A(﹣8,0),B(﹣8,4),C(0,4),
反比例函数 y=k
x
的图象分别与线段 AB,BC交于点 D,E,连接 DE.若点 B关于 DE的对
称点恰好在 OA上,则 k=
参考答案:
例题 1:见分析 变式练习 1、3
题型一:例题 2、(﹣ ,1)
变式练习 2、
5
109
变式练习 3、
2
5
题型二:1、A 2、B
题型三:1、2 2、5
中考在线:1、6 2、(2,7) 3、
4、
5 5、A.
6、
(﹣2 ,6)
7、 8、 3-32 9、﹣12
同课章节目录
