北京课改版八年级数学下册 14.1.2 函数的概念 课件(第一课时共69张PPT)
文档属性
| 名称 | 北京课改版八年级数学下册 14.1.2 函数的概念 课件(第一课时共69张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 00:00:00 | ||
图片预览










文档简介
(共69张PPT)
初二年级 数学
函数的概念(第一课时)
世界上的万事万物都在不停地发展着、变化着,在这些发展和变化的过程中,存在着各式各样相关联的量.
下面所列举的每一项活动中,都存在着哪些互相关联的量?这些量中,哪些量是在不断变化的?哪些量是保持不变的?
例如,在商店里购物,飞机从北京飞往上海……
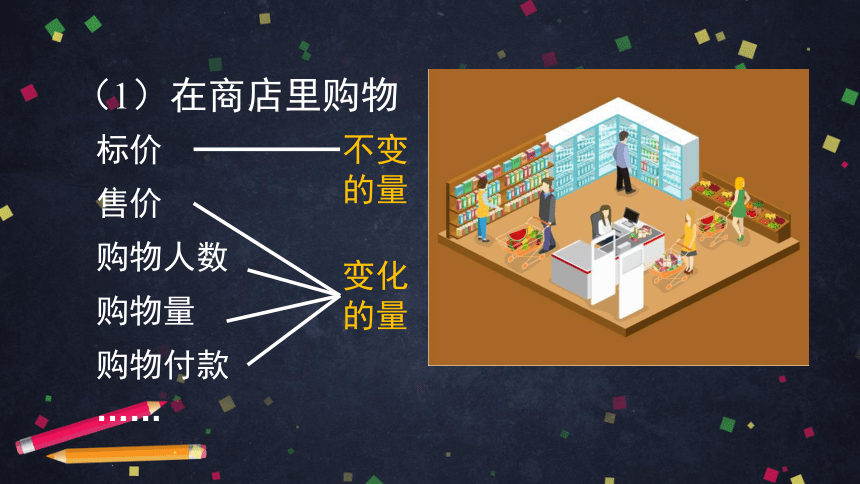
(1)在商店里购物
不变
的量
变化
的量
购物人数
标价
售价
购物量
购物付款
……
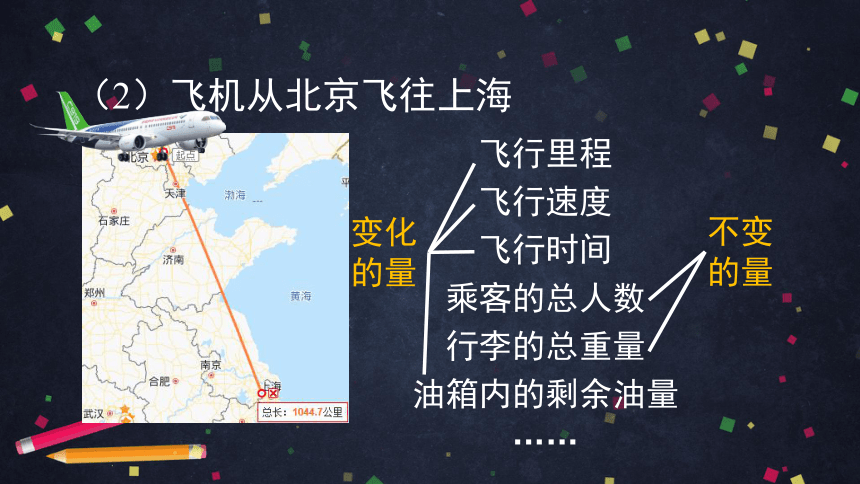
(2)飞机从北京飞往上海
飞行里程
飞行速度
飞行时间
乘客的总人数
行李的总重量
油箱内的剩余油量
……
不变
的量
变化
的量
变量和常量
一般地,在一个变化的过程中,可以取不同数值的量叫做变量,只取同一数值的量叫做常量.
例1 判断下面各题中,哪些是常量,哪些是变量:
(1)用公式 C = πd 计算圆的周长;
C -->变量
d -->变量
π -->常量
变化关联
例1 判断下面各题中,哪些是常量,哪些是变量:
(2)用公式 s = vt 解决百米赛跑有关问题;
从跑完100米角度看
s -->常量
v -->变量
t -->变量
例1 判断下面各题中,哪些是常量,哪些是变量:
(2)用公式 s = vt 解决百米赛跑有关问题;
假定某选手10米/秒匀速奔跑
s -->变量
v -->常量
t -->变量
例1 判断下面各题中,哪些是常量,哪些是变量:
(2)用公式 s = vt 解决百米赛跑有关问题;
从跑了5秒看谁领先
s -->变量
v -->变量
t -->常量
例1 判断下面各题中,哪些是常量,哪些是变量:
(2)用公式 s = vt 解决百米赛跑有关问题;
变量和变量之间的对应关系常是在常量存在的条件下发生的,而且一个量在一定条件下可能是变量,在另一定条件下又可能是常量.
例1 判断下面各题中,哪些是常量,哪些是变量:
(3)一个容积是10万升的储油罐内储满了汽油,如果每天运出4 000升,计算储油罐内的剩余油量.
起始油量
运油天数
累计运出油量
储油罐容积
日运出油量
剩余油量
常量
变量
10万升
4 000升/天
例1 判断下面各题中,哪些是常量,哪些是变量:
剩余油量=起始油量﹣日运出油量×天数
常量
变量
(3)一个容积是10万升的储油罐内储满了汽油,如果每天运出4 000升,计算储油罐内的剩余油量.
变式:一个容积是10万升的储油罐内储存了9万升汽油,如果每天运出4 000升,计算储油罐内的剩余油量.
例1 判断下面各题中,哪些是常量,哪些是变量:
剩余油量=起始油量﹣日运出油量×天数
常量
变量
9万升
4 000升/天
变量和常量的确定
1.分析变化过程,找出量;
2.找出各量之间的关联;
3.指出解决问题所涉及的变量和常量.
注:有些常量是显而易见的,有些是长期摸索后发现的;变化关联看问题有助发现常量;变量关系常是在常量存在的条件下发生的,一定条件下常量与变量是相对的.
在飞机飞行的过程中,起飞后的飞行里程与起飞后的飞行时间有什么关系呢?
若飞机的平均航速是14 km/min,请填写下表:
飞行时间(min)
飞行里程(km)
10
20
30
40
50
60
140
280
420
560
700
840
飞行里程=飞行速度×飞行时间
“飞行时间”的每一个值,
“飞行里程”都有唯一确定的值和它对应.
在飞机飞行的过程中,起飞后的剩余油量与起飞后的飞行时间有什么关系呢?
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
飞行时间(min)
剩余油量(t)
10
20
30
40
50
60
12
11
10
9
8
7
剩余油量=起飞油量﹣耗油速度×飞行时间
“飞行时间”的每一个值,
“剩余油量”都有唯一确定的值和它对应.
函数的定义
一般地,在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y 是x的函数.
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(1) y:正方形的面积.x:这个正方形的周长.
(2) y:长方形的面积.x:这个长方形一边的长.
(3) y:一个正数的平方根. x:这个正数.
(4) y:一个正数的算术平方根. x:这个正数.
是
分析:
4
8
12
16
20
24
1
2
3
4
5
6
周长x
边长
面积y
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(1) y:正方形的面积.x:这个正方形的周长.
1
4
9
16
25
36
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(2) y:长方形的面积.x:这个长方形一边的长.
分析:
1
?
一边x
另一边
面积y
?
不确定
不确定
不是
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(3) y:一个正数的平方根. x:这个正数.
分析:
正数x
平方根y
不是
1
2
3
4
5
对于每一个x值,y值都不唯一.
是
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(4) y:一个正数的算术平方根. x:这个正数.
分析:
x
y
1
2
3
4
5
对于每一个x值,y值都唯一确定.
函数关系的确定
1.分析所研究的量谁是自变量,谁是因变量;
2.找出与所研究量相关联的量;
3.分析自变量每取一个值,因变量是否有唯一确定的值与之对应,并做出判断.
注:不确定,通常是有其它变量参与其中.
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(1) y:正方形的面积.x:这个正方形的周长.
(2) y:长方形的面积.x:这个长方形一边的长.
(3) y:一个正数的平方根. x:这个正数.
(4) y:一个正数的算术平方根. x:这个正数.
是
分析:
4
8
12
16
20
24
周长x
1
2
3
4
5
6
边长
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(1) y:正方形的面积.x:这个正方形的周长.
面积y
1
4
9
16
25
36
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(2) y:长方形的面积.x:这个长方形一边的长.
分析:
1
?
面积y
一边x
另一边
不确定
不确定
不是
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(3) y:一个正数的平方根. x:这个正数.
分析:
y
x
是
1
2
3
4
5
1
4
9
16
25
是
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(4) y:一个正数的算术平方根. x:这个正数.
分析:
y
x
1
2
3
4
5
1
4
9
16
25
对比一下
例2 x是不是y的函数:
(1) 是
(2) 不是
(3) 是
(4) 是
例2 y是不是x的函数:
(1) 是
(2) 不是
(3) 不是
(4) 是
x取值,y唯一确定
y取值,x唯一确定
线索回顾
实际问题
量
运动
变化
常量
变量
两变量
对应关系
函数
…
…
设计
研究
唯一确定
作业
本章第一节函数中的前两个练习
作业
祝同学们越来越优秀!
初二年级 数学
函数的概念(第二课时)
回顾
实际问题
量
运动
变化
常量
变量
两变量
对应关系
函数
…
…
设计
研究
唯一确定
函数的定义
一般地,在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y 是x的函数.
函数有什么意义或用处呢?
1. 你能预测飞机能飞行多久吗?
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
飞行时间(min)
剩余油量(t)
10
20
30
40
50
60
12
11
10
9
8
7
剩余油量=起飞油量﹣耗油速度×飞行时间
飞行时间(min)
剩余油量(t)
70
80
90
100
110
120
6
5
4
3
2
1
剩余油量=起飞油量﹣耗油速度×飞行时间
130
0
1. 你能预测飞机能飞行多久吗?
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
设飞行时间为x(min),剩余油量为y(t),则函数关系可以写成:
剩余油量=起飞油量-耗油速度×飞行时间
1. 你能预测飞机能飞行多久吗?
y=13﹣0.1x.
令y=0,于是13﹣0.1x=0,解得x=130.
2. 画周长为10cm的等腰三角形.
常量
变量
周长
腰长
底长
面积
顶角
底角
变量关系
2. 画周长为10cm的等腰三角形.
设腰长为xcm,底长为ycm,则
腰长
底长
腰长x
底长y
3
4
4
2
y=10﹣2x
x
x
y
2. 画周长为10cm的等腰三角形.
腰长x
底长y
1
2
3
4
5
8
6
4
2
0
x﹣x<10﹣2x2.5设腰长为xcm,底长为ycm,则
y=10﹣2x
x
x
y
2. 画周长为10cm的等腰三角形.
(2.5y=10﹣2x
自变量取值范围不可缺少
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
设飞行时间为x(min),剩余油量为y(t),则函数关系可以写成:y=13﹣0.1x,
令y=0,于是13-0.1x=0,解得x=130.
剩余油量=起飞油量-耗油速度×飞行时间
0≤飞行时间<130
函数的概念
一般地,在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y 是x的函数.
自变量的取值范围
例1 全校共有2 530名学生.现自愿购买运动服,每人限购一套,若每套85元.请问购买总金额是购买运动服人数的函数吗?自变量的取值范围是多少?
购买总金额=每套价格×购买套数
设购买人数为x人,购买总金额为y元,每人限购一套,则
对于x的每一个值,y都有唯一确定的值和它对应,故购买总金额是购买运动服人数的函数.
y=85x.
0≤x≤2 530,
且x为整数.
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
, , ,…
89
4
5
x
﹣5
0
1
…
…
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
, , ,…
2
x
﹣5
0
1
…
…
, , ,…
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
x
﹣5
0
1
…
…
, , ,…
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
(1)若把x 看做自变量,把代数式的值y 看做因变量,那么y 是x 的函数吗?
是
, , ,…
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
(2)自变量x 的取值有限制吗?
代数式有意义
整式
分式
二次根式
单项式
多项式
除数不为0
负数不能开平方
分母不等于0
被开方数是非负数
任意实数
(1)
例3 求下列函数中自变量x 的取值范围:
(2)
(3)
(4)
(5)
(1)
例3 求下列函数中自变量x 的取值范围:
解:
自变量x 的取值范围是任意实数.
(2)
例3 求下列函数中自变量x 的取值范围:
由于3x﹣2≠0,
解:
所以自变量x 的取值范围是 .
(3)
例3 求下列函数中自变量x 的取值范围:
由于5﹣3x≥0,
解:
所以自变量x 的取值范围是 .
(4)
例3 求下列函数中自变量x 的取值范围:
解:自变量x 应满足的条件是
解得
所以自变量x 的取值范围是 .
(5)
例3 求下列函数中自变量x 的取值范围:
解:自变量x 应满足的条件是
解得
所以自变量x 的取值范围是 .
自变量取值范围的确定
式子有意义
符合实际意义
整式
分式
二次根式
分母不等于0
被开方数是非负数
任意实数
练习 搭1个正方形需要4根火柴棍.
(1) 按照图中的方式,搭2个正方形需要几根火柴棍?搭3个正方形呢?
10
7
4
(2) 如果用x 表示所搭正方形的个数,搭x 个这样的正方形需要y 根火柴棍,那么y 与x 之间存在函数关系吗?
10
7
4
每多用3根火柴,便可多搭出1个正方形.
y=4+3(x﹣1)
=3x+1
(x为正整数)
(3) 小明说,用了92根火柴这样搭,正好搭成30个正方形.他说得对吗?
y=3x+1
当x=30时,y=3×30+1=91≠92.
当y=92时,x=(92﹣1)÷3≈30.3≠30.
(x为正整数)
故小明说得不对.
函数的概念
一般地,在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y 是x的函数.
自变量的取值范围
唯一确定对应关系
?
作业
本章第一单元函数习题中基础3题和提升1题
作业
本章第一单元函数习题中基础3题和提升1题
祝同学们学习快乐!
初二年级 数学
函数的概念(第一课时)
世界上的万事万物都在不停地发展着、变化着,在这些发展和变化的过程中,存在着各式各样相关联的量.
下面所列举的每一项活动中,都存在着哪些互相关联的量?这些量中,哪些量是在不断变化的?哪些量是保持不变的?
例如,在商店里购物,飞机从北京飞往上海……
(1)在商店里购物
不变
的量
变化
的量
购物人数
标价
售价
购物量
购物付款
……
(2)飞机从北京飞往上海
飞行里程
飞行速度
飞行时间
乘客的总人数
行李的总重量
油箱内的剩余油量
……
不变
的量
变化
的量
变量和常量
一般地,在一个变化的过程中,可以取不同数值的量叫做变量,只取同一数值的量叫做常量.
例1 判断下面各题中,哪些是常量,哪些是变量:
(1)用公式 C = πd 计算圆的周长;
C -->变量
d -->变量
π -->常量
变化关联
例1 判断下面各题中,哪些是常量,哪些是变量:
(2)用公式 s = vt 解决百米赛跑有关问题;
从跑完100米角度看
s -->常量
v -->变量
t -->变量
例1 判断下面各题中,哪些是常量,哪些是变量:
(2)用公式 s = vt 解决百米赛跑有关问题;
假定某选手10米/秒匀速奔跑
s -->变量
v -->常量
t -->变量
例1 判断下面各题中,哪些是常量,哪些是变量:
(2)用公式 s = vt 解决百米赛跑有关问题;
从跑了5秒看谁领先
s -->变量
v -->变量
t -->常量
例1 判断下面各题中,哪些是常量,哪些是变量:
(2)用公式 s = vt 解决百米赛跑有关问题;
变量和变量之间的对应关系常是在常量存在的条件下发生的,而且一个量在一定条件下可能是变量,在另一定条件下又可能是常量.
例1 判断下面各题中,哪些是常量,哪些是变量:
(3)一个容积是10万升的储油罐内储满了汽油,如果每天运出4 000升,计算储油罐内的剩余油量.
起始油量
运油天数
累计运出油量
储油罐容积
日运出油量
剩余油量
常量
变量
10万升
4 000升/天
例1 判断下面各题中,哪些是常量,哪些是变量:
剩余油量=起始油量﹣日运出油量×天数
常量
变量
(3)一个容积是10万升的储油罐内储满了汽油,如果每天运出4 000升,计算储油罐内的剩余油量.
变式:一个容积是10万升的储油罐内储存了9万升汽油,如果每天运出4 000升,计算储油罐内的剩余油量.
例1 判断下面各题中,哪些是常量,哪些是变量:
剩余油量=起始油量﹣日运出油量×天数
常量
变量
9万升
4 000升/天
变量和常量的确定
1.分析变化过程,找出量;
2.找出各量之间的关联;
3.指出解决问题所涉及的变量和常量.
注:有些常量是显而易见的,有些是长期摸索后发现的;变化关联看问题有助发现常量;变量关系常是在常量存在的条件下发生的,一定条件下常量与变量是相对的.
在飞机飞行的过程中,起飞后的飞行里程与起飞后的飞行时间有什么关系呢?
若飞机的平均航速是14 km/min,请填写下表:
飞行时间(min)
飞行里程(km)
10
20
30
40
50
60
140
280
420
560
700
840
飞行里程=飞行速度×飞行时间
“飞行时间”的每一个值,
“飞行里程”都有唯一确定的值和它对应.
在飞机飞行的过程中,起飞后的剩余油量与起飞后的飞行时间有什么关系呢?
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
飞行时间(min)
剩余油量(t)
10
20
30
40
50
60
12
11
10
9
8
7
剩余油量=起飞油量﹣耗油速度×飞行时间
“飞行时间”的每一个值,
“剩余油量”都有唯一确定的值和它对应.
函数的定义
一般地,在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y 是x的函数.
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(1) y:正方形的面积.x:这个正方形的周长.
(2) y:长方形的面积.x:这个长方形一边的长.
(3) y:一个正数的平方根. x:这个正数.
(4) y:一个正数的算术平方根. x:这个正数.
是
分析:
4
8
12
16
20
24
1
2
3
4
5
6
周长x
边长
面积y
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(1) y:正方形的面积.x:这个正方形的周长.
1
4
9
16
25
36
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(2) y:长方形的面积.x:这个长方形一边的长.
分析:
1
?
一边x
另一边
面积y
?
不确定
不确定
不是
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(3) y:一个正数的平方根. x:这个正数.
分析:
正数x
平方根y
不是
1
2
3
4
5
对于每一个x值,y值都不唯一.
是
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断y是不是x的函数:
(4) y:一个正数的算术平方根. x:这个正数.
分析:
x
y
1
2
3
4
5
对于每一个x值,y值都唯一确定.
函数关系的确定
1.分析所研究的量谁是自变量,谁是因变量;
2.找出与所研究量相关联的量;
3.分析自变量每取一个值,因变量是否有唯一确定的值与之对应,并做出判断.
注:不确定,通常是有其它变量参与其中.
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(1) y:正方形的面积.x:这个正方形的周长.
(2) y:长方形的面积.x:这个长方形一边的长.
(3) y:一个正数的平方根. x:这个正数.
(4) y:一个正数的算术平方根. x:这个正数.
是
分析:
4
8
12
16
20
24
周长x
1
2
3
4
5
6
边长
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(1) y:正方形的面积.x:这个正方形的周长.
面积y
1
4
9
16
25
36
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(2) y:长方形的面积.x:这个长方形一边的长.
分析:
1
?
面积y
一边x
另一边
不确定
不确定
不是
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(3) y:一个正数的平方根. x:这个正数.
分析:
y
x
是
1
2
3
4
5
1
4
9
16
25
是
例2 下面每题都给出了某个变化过程中的两个变量 x和y,判断x是不是y的函数:
(4) y:一个正数的算术平方根. x:这个正数.
分析:
y
x
1
2
3
4
5
1
4
9
16
25
对比一下
例2 x是不是y的函数:
(1) 是
(2) 不是
(3) 是
(4) 是
例2 y是不是x的函数:
(1) 是
(2) 不是
(3) 不是
(4) 是
x取值,y唯一确定
y取值,x唯一确定
线索回顾
实际问题
量
运动
变化
常量
变量
两变量
对应关系
函数
…
…
设计
研究
唯一确定
作业
本章第一节函数中的前两个练习
作业
祝同学们越来越优秀!
初二年级 数学
函数的概念(第二课时)
回顾
实际问题
量
运动
变化
常量
变量
两变量
对应关系
函数
…
…
设计
研究
唯一确定
函数的定义
一般地,在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y 是x的函数.
函数有什么意义或用处呢?
1. 你能预测飞机能飞行多久吗?
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
飞行时间(min)
剩余油量(t)
10
20
30
40
50
60
12
11
10
9
8
7
剩余油量=起飞油量﹣耗油速度×飞行时间
飞行时间(min)
剩余油量(t)
70
80
90
100
110
120
6
5
4
3
2
1
剩余油量=起飞油量﹣耗油速度×飞行时间
130
0
1. 你能预测飞机能飞行多久吗?
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
设飞行时间为x(min),剩余油量为y(t),则函数关系可以写成:
剩余油量=起飞油量-耗油速度×飞行时间
1. 你能预测飞机能飞行多久吗?
y=13﹣0.1x.
令y=0,于是13﹣0.1x=0,解得x=130.
2. 画周长为10cm的等腰三角形.
常量
变量
周长
腰长
底长
面积
顶角
底角
变量关系
2. 画周长为10cm的等腰三角形.
设腰长为xcm,底长为ycm,则
腰长
底长
腰长x
底长y
3
4
4
2
y=10﹣2x
x
x
y
2. 画周长为10cm的等腰三角形.
腰长x
底长y
1
2
3
4
5
8
6
4
2
0
x﹣x<10﹣2x
y=10﹣2x
x
x
y
2. 画周长为10cm的等腰三角形.
(2.5
自变量取值范围不可缺少
若起飞时油量为13 t,飞行时耗油0. 1 t/min:
设飞行时间为x(min),剩余油量为y(t),则函数关系可以写成:y=13﹣0.1x,
令y=0,于是13-0.1x=0,解得x=130.
剩余油量=起飞油量-耗油速度×飞行时间
0≤飞行时间<130
函数的概念
一般地,在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y 是x的函数.
自变量的取值范围
例1 全校共有2 530名学生.现自愿购买运动服,每人限购一套,若每套85元.请问购买总金额是购买运动服人数的函数吗?自变量的取值范围是多少?
购买总金额=每套价格×购买套数
设购买人数为x人,购买总金额为y元,每人限购一套,则
对于x的每一个值,y都有唯一确定的值和它对应,故购买总金额是购买运动服人数的函数.
y=85x.
0≤x≤2 530,
且x为整数.
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
, , ,…
89
4
5
x
﹣5
0
1
…
…
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
, , ,…
2
x
﹣5
0
1
…
…
, , ,…
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
x
﹣5
0
1
…
…
, , ,…
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
(1)若把x 看做自变量,把代数式的值y 看做因变量,那么y 是x 的函数吗?
是
, , ,…
例2 当x 的值分别取﹣5,0,1,…时,求下列代数式的值.
(2)自变量x 的取值有限制吗?
代数式有意义
整式
分式
二次根式
单项式
多项式
除数不为0
负数不能开平方
分母不等于0
被开方数是非负数
任意实数
(1)
例3 求下列函数中自变量x 的取值范围:
(2)
(3)
(4)
(5)
(1)
例3 求下列函数中自变量x 的取值范围:
解:
自变量x 的取值范围是任意实数.
(2)
例3 求下列函数中自变量x 的取值范围:
由于3x﹣2≠0,
解:
所以自变量x 的取值范围是 .
(3)
例3 求下列函数中自变量x 的取值范围:
由于5﹣3x≥0,
解:
所以自变量x 的取值范围是 .
(4)
例3 求下列函数中自变量x 的取值范围:
解:自变量x 应满足的条件是
解得
所以自变量x 的取值范围是 .
(5)
例3 求下列函数中自变量x 的取值范围:
解:自变量x 应满足的条件是
解得
所以自变量x 的取值范围是 .
自变量取值范围的确定
式子有意义
符合实际意义
整式
分式
二次根式
分母不等于0
被开方数是非负数
任意实数
练习 搭1个正方形需要4根火柴棍.
(1) 按照图中的方式,搭2个正方形需要几根火柴棍?搭3个正方形呢?
10
7
4
(2) 如果用x 表示所搭正方形的个数,搭x 个这样的正方形需要y 根火柴棍,那么y 与x 之间存在函数关系吗?
10
7
4
每多用3根火柴,便可多搭出1个正方形.
y=4+3(x﹣1)
=3x+1
(x为正整数)
(3) 小明说,用了92根火柴这样搭,正好搭成30个正方形.他说得对吗?
y=3x+1
当x=30时,y=3×30+1=91≠92.
当y=92时,x=(92﹣1)÷3≈30.3≠30.
(x为正整数)
故小明说得不对.
函数的概念
一般地,在一个变化过程中,有两个变量x和y,对于变量x的每一个值,变量y都有唯一确定的值和它对应,我们就把x称为自变量,y称为因变量,y 是x的函数.
自变量的取值范围
唯一确定对应关系
?
作业
本章第一单元函数习题中基础3题和提升1题
作业
本章第一单元函数习题中基础3题和提升1题
祝同学们学习快乐!
同课章节目录
