人教版八年级下册数学 16.1二次根式概念及性质课件(2课时 共72张PPT)
文档属性
| 名称 | 人教版八年级下册数学 16.1二次根式概念及性质课件(2课时 共72张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 17:10:16 | ||
图片预览









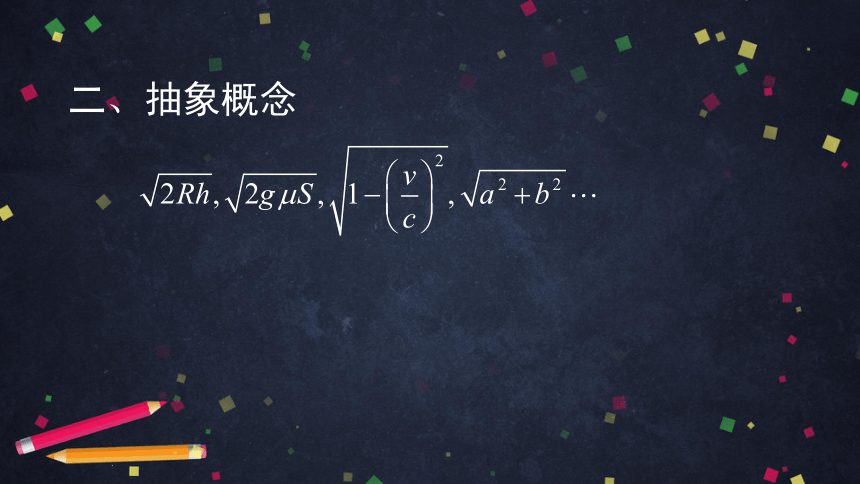


文档简介
(共72张PPT)
二次根式的概念及性质(第一课时)
初二年级 数学
一、引入概念
二次根式
整式、分式
字母表示数
数式通性
运算 数与字母运算 定义
加/减
乘
除
乘方
开方
单项式
多项式
整式
一般地,如果A , B表示两个整式,并且
B中含有字母,那么式子
叫做分式(fraction).
分式定义
运算 数与字母运算 定义
加/减
乘
除
乘方
开方
单项式
多项式
整式
?
分式
(分母含字母)
电视塔越高,从塔顶发射出的电磁波传播得越远,从而能收看到电视节目的区域就越广.电视塔高h(单位:km)与电视节目信号的传播半径r(单位:km )之间存在近似关系r=
其中R是地球半径, R≈6400km .
实际应用
汽车刹车时的速度v与汽车刹车后滑行的距离S之间存在关系 .其中, g是常数9.8 , μ是摩擦系数.
在解决交通肇事问题时,可以通过测量刹车后车轮滑过的距离计算车辆行驶的速度.
实际应用
爱因斯坦的相对论家喻户晓.它是关于时空和引力的理论.根据爱因斯坦的相对论, 地球上的1秒钟,宇宙飞船内只经过 秒.
其中, v是宇宙飞船的速度,
c是光速(约每秒30万千米) .
实际应用
一元二次方程的
求根公式:
直角三角形的斜边
a
b
c
数学应用
二、抽象概念
算术平方根:
一般地,如果一个正数x的平方等于a, 即x2=a , 那么这个正数x叫做a的算术平方根 .
规定:0的算术平方根是0 .
被开方数
二次根号
一般地, 我们把形如 的式子
叫做二次根式.
二次根式:
①含有二次根号.
②a可以是数,也可以是含字母的式子.
注意:
想一想
在二次根式的定义中,为什么要求“a≥0”?
“数式通性”:负数没有算术平方根.
若a是常数,则a为非负数;
若a是式子,则式子的值是非负的.
反过来:
当a > 0时, 0;
当a = 0时, 0.
=
想一想
二次根式的双重非负性:
归纳
如5 ,
它们都是用基本运算符号(基本运算包括加、减、
乘、除、乘方和开方)把数或表示数的字母连接起
来的式子,我们称这样的式子为代数式.
(1)下列式子一定是二次根式的是 ( ) .
(A)
(B)
(C)
(D)
例1 根据二次根式定义进行判断
C
(2)当x是怎样的实数时,下列各式在实数范围内有意义?
例1 根据二次根式定义进行判断
解:
解:
例1 根据二次根式定义进行判断
解:
解:
(2)当x是怎样的实数时,下列各式在实数范围内有意义?
例1 根据二次根式定义进行判断
解:
解:
(2)当x是怎样的实数时,下列各式在实数范围内有意义?
例1 根据二次根式定义进行判断
解:
解:
(2)当x是怎样的实数时,下列各式在实数范围内有意义?
总结:求使代数式有意义的字母取值范围的条件:
1.
二次根式型: 被开方数≥0;
2.
分式型: 分母 0 ;
3.
零指数幂型: 底数 0 ;
4. 复合型:
各部分取值范围的公共部分.
例2 二次根式双重非负性的应用
(1)当x取何值时, 的值最小,
最小值是多少?
≥0
0
解:
的值最小.
即当 时, 的值最小,
最小值是3.
,
当 时,
例2 二次根式双重非负性的应用
(2)若 , 则a+b?c= .
分析:
0 + 0 = 0
≥0
≥0
≥0
0 + 0 + 0 = 0
a =?2 , b=3 , c=?4.
a +b?c=5.
5
总结:二次根式的双重非负性
1. 二次根式的最小值为0;
2.常见的具有非负性的式子有:
若 , 则a=b=c=0.
(1)若 是正整数, 则n的最大整数值是 .
例3 二次根式双重非负性的应用
n取最大整数
完全平方数
正整数
10-n是非0的
最小的完全平方数
分析:
9
10-n =1
(2)已知a满足 ,
则 .
例3 二次根式双重非负性的应用
例3 二次根式双重非负性的应用
分析:
(2)已知a满足 ,
则 .
例3 二次根式双重非负性的应用
2021
分析:
例4 二次根式双重非负性的应用
已知:a与b为等腰三角形的两边长,且满足等式
求这个等腰三角形的周长.
分析:
(舍)
例4 二次根式双重非负性的应用
解:由题意可得
解得
a ,b为等腰三角形的两边长,
2+2=4(舍) ,
等腰三角形周长为4+4+2=10.
三边为2,2,4或4,4,2.
提升练习
1.下列式子中是二次根式的有( ) .
①
;②
;③
④
⑤ .
(m>2);
;
④ ⑤
提升练习
x 不可以取3的是( ) .
(A) 只有① (B) 只有② (C) ①和② (D) ①和③
C
2.在下列式子:①
, ②(x-3)0, ③
中,
归纳小结
1.二次根式的定义
形如 (a≥0)的式子叫做二次根式.
2.二次根式的性质
(1)双重非负性:
.
作业
1.当a是怎样的实数时,下列各式在实数范围内有意义?
2.当x是怎样的实数时,下列各式在实数范围内有意义?
3.(1)已知 是整数,求自然数n所有可能的值;
(2)已知 是整数,求正整数n的最小值.
祝同学们越来越优秀!
二次根式的概念及性质(第二课时)
初二年级 数学
复习回顾
1.二次根式的定义
形如 (a≥0)的式子叫做二次根式.
2.二次根式的性质
(1)双重非负性:
.
乘方 开方
互逆
乘 除
互逆
加 减
互逆
猜想:
规律探究
验证猜想:
猜想2:
猜想1:
算术平方根的定义:如果一个正数x的平方等于a, 即x2=a,
那么这个正数x叫做a的算术平方根. 0的算术平方根是0.
是4的算术平方根,因此它的平方等于4, 即 ;
4
验证猜想1:
4
2
0
是4的算术平方根,因此它的平方等于4 , 即 ;
是2的算术平方根,因此它的平方等于2 , 即 ;
是 的算术平方根,因此它的平方等于 , 即 ;
是0的算术平方根,因此它的平方等于0 , 即
.
验证猜想1:
是a的算术平方根,因此它的平方等于a ,即
4
2
0
验证猜想1:
是4的算术平方根,因此它的平方等于4 , 即 ;…
1.双重非负性:
2.
二次根式性质:
验证猜想:
猜想2:
猜想1:
验证猜想:
猜想2:
二次根式性质2:
2
0.1
0
是一个非负数,它的平方等于 所以
是一个非负数,它的平方等于 所以
是一个非负数,它的平方等于 所以
是一个非负数,它的平方等于 ,所以
验证猜想2:
2
0.1
0
是一个非负数,它的平方等于
验证猜想2:
是一个非负数,它的平方等于 所以
验证猜想2:
不成立.
反例:
是一个非负数,它的平方等于 所以
2
0.1
2
0.1
0
是一个非负数,它的平方等于
验证猜想2:
是一个非负数,它的平方等于 所以
2
0.1
0
验证猜想2:
是一个非负数,它的平方等于 所以
2
0.1
0
是一个非负数,它的平方等于
验证猜想2:
是一个非负数,它的平方等于 所以
2
0.1
0
是一个非负数,它的平方等于 ,所以
验证猜想2:
是一个非负数,它的平方等于 所以
2
0.1
0
验证猜想2:
是一个非负数,它的平方等于 所以
1.双重非负性:
2.
3.
二次根式性质:
验证猜想:
二次根式性质2:
二次根式性质3:
性质
含义
a的取值
运算结果
a为任意实数
一个数的平方的算术平方根等于这个数的绝对值
一个非负数算术平方根的平方等于它本身
运用性质
例1 运用性质进行计算
(1)
运用 进行计算.
运用性质
(2)
例1 运用性质进行计算
运用 进行计算.
运用性质
(2)
例1 运用性质进行计算
运用 进行计算.
运用性质
若
, 则a的取值范围是( ).
(B)
(C)
(D)
(A)
D
法1:
法2:
例1 运用性质进行计算
(3)
运用性质
(1)判断下列等式是否成立:
例2 性质运用的辨析
运用性质
(2)对于题目:化简并求值:
其中 .
乙的解答如下:
甲的解答如下:
例2 性质运用的辨析
乙的解答:
甲的解答:
逆用性质
逆用性质
任意一个非负数都能写成平方的形式.
一个非负数算术平方根的平方等于它本身.
逆用性质
任意一个非负数都能化成二次根式的形式.
一个数的平方的算术平方根等于这个数的绝对值.
任意一个非负数都能化成平方的形式.
任意一个非负数都能化成二次根式的形式.
逆用性质
归纳小结
1. 二次根式的定义:
形如 (a≥0)的式子.
2. 二次根式的性质
(1)双重非负性:
(2)
(3)
作业
1.计算:
2.把下列非负数分别写成一个非负数的平方的形式:
3.一个圆柱体的高为10 ,体积为V.求它的底面半径r(用含V的
代数式表示),并分别求当V =5π , 10π和20π时 ,
底面半径r的大小.
祝同学们越来越优秀!
二次根式的概念及性质(第一课时)
初二年级 数学
一、引入概念
二次根式
整式、分式
字母表示数
数式通性
运算 数与字母运算 定义
加/减
乘
除
乘方
开方
单项式
多项式
整式
一般地,如果A , B表示两个整式,并且
B中含有字母,那么式子
叫做分式(fraction).
分式定义
运算 数与字母运算 定义
加/减
乘
除
乘方
开方
单项式
多项式
整式
?
分式
(分母含字母)
电视塔越高,从塔顶发射出的电磁波传播得越远,从而能收看到电视节目的区域就越广.电视塔高h(单位:km)与电视节目信号的传播半径r(单位:km )之间存在近似关系r=
其中R是地球半径, R≈6400km .
实际应用
汽车刹车时的速度v与汽车刹车后滑行的距离S之间存在关系 .其中, g是常数9.8 , μ是摩擦系数.
在解决交通肇事问题时,可以通过测量刹车后车轮滑过的距离计算车辆行驶的速度.
实际应用
爱因斯坦的相对论家喻户晓.它是关于时空和引力的理论.根据爱因斯坦的相对论, 地球上的1秒钟,宇宙飞船内只经过 秒.
其中, v是宇宙飞船的速度,
c是光速(约每秒30万千米) .
实际应用
一元二次方程的
求根公式:
直角三角形的斜边
a
b
c
数学应用
二、抽象概念
算术平方根:
一般地,如果一个正数x的平方等于a, 即x2=a , 那么这个正数x叫做a的算术平方根 .
规定:0的算术平方根是0 .
被开方数
二次根号
一般地, 我们把形如 的式子
叫做二次根式.
二次根式:
①含有二次根号.
②a可以是数,也可以是含字母的式子.
注意:
想一想
在二次根式的定义中,为什么要求“a≥0”?
“数式通性”:负数没有算术平方根.
若a是常数,则a为非负数;
若a是式子,则式子的值是非负的.
反过来:
当a > 0时, 0;
当a = 0时, 0.
=
想一想
二次根式的双重非负性:
归纳
如5 ,
它们都是用基本运算符号(基本运算包括加、减、
乘、除、乘方和开方)把数或表示数的字母连接起
来的式子,我们称这样的式子为代数式.
(1)下列式子一定是二次根式的是 ( ) .
(A)
(B)
(C)
(D)
例1 根据二次根式定义进行判断
C
(2)当x是怎样的实数时,下列各式在实数范围内有意义?
例1 根据二次根式定义进行判断
解:
解:
例1 根据二次根式定义进行判断
解:
解:
(2)当x是怎样的实数时,下列各式在实数范围内有意义?
例1 根据二次根式定义进行判断
解:
解:
(2)当x是怎样的实数时,下列各式在实数范围内有意义?
例1 根据二次根式定义进行判断
解:
解:
(2)当x是怎样的实数时,下列各式在实数范围内有意义?
总结:求使代数式有意义的字母取值范围的条件:
1.
二次根式型: 被开方数≥0;
2.
分式型: 分母 0 ;
3.
零指数幂型: 底数 0 ;
4. 复合型:
各部分取值范围的公共部分.
例2 二次根式双重非负性的应用
(1)当x取何值时, 的值最小,
最小值是多少?
≥0
0
解:
的值最小.
即当 时, 的值最小,
最小值是3.
,
当 时,
例2 二次根式双重非负性的应用
(2)若 , 则a+b?c= .
分析:
0 + 0 = 0
≥0
≥0
≥0
0 + 0 + 0 = 0
a =?2 , b=3 , c=?4.
a +b?c=5.
5
总结:二次根式的双重非负性
1. 二次根式的最小值为0;
2.常见的具有非负性的式子有:
若 , 则a=b=c=0.
(1)若 是正整数, 则n的最大整数值是 .
例3 二次根式双重非负性的应用
n取最大整数
完全平方数
正整数
10-n是非0的
最小的完全平方数
分析:
9
10-n =1
(2)已知a满足 ,
则 .
例3 二次根式双重非负性的应用
例3 二次根式双重非负性的应用
分析:
(2)已知a满足 ,
则 .
例3 二次根式双重非负性的应用
2021
分析:
例4 二次根式双重非负性的应用
已知:a与b为等腰三角形的两边长,且满足等式
求这个等腰三角形的周长.
分析:
(舍)
例4 二次根式双重非负性的应用
解:由题意可得
解得
a ,b为等腰三角形的两边长,
2+2=4(舍) ,
等腰三角形周长为4+4+2=10.
三边为2,2,4或4,4,2.
提升练习
1.下列式子中是二次根式的有( ) .
①
;②
;③
④
⑤ .
(m>2);
;
④ ⑤
提升练习
x 不可以取3的是( ) .
(A) 只有① (B) 只有② (C) ①和② (D) ①和③
C
2.在下列式子:①
, ②(x-3)0, ③
中,
归纳小结
1.二次根式的定义
形如 (a≥0)的式子叫做二次根式.
2.二次根式的性质
(1)双重非负性:
.
作业
1.当a是怎样的实数时,下列各式在实数范围内有意义?
2.当x是怎样的实数时,下列各式在实数范围内有意义?
3.(1)已知 是整数,求自然数n所有可能的值;
(2)已知 是整数,求正整数n的最小值.
祝同学们越来越优秀!
二次根式的概念及性质(第二课时)
初二年级 数学
复习回顾
1.二次根式的定义
形如 (a≥0)的式子叫做二次根式.
2.二次根式的性质
(1)双重非负性:
.
乘方 开方
互逆
乘 除
互逆
加 减
互逆
猜想:
规律探究
验证猜想:
猜想2:
猜想1:
算术平方根的定义:如果一个正数x的平方等于a, 即x2=a,
那么这个正数x叫做a的算术平方根. 0的算术平方根是0.
是4的算术平方根,因此它的平方等于4, 即 ;
4
验证猜想1:
4
2
0
是4的算术平方根,因此它的平方等于4 , 即 ;
是2的算术平方根,因此它的平方等于2 , 即 ;
是 的算术平方根,因此它的平方等于 , 即 ;
是0的算术平方根,因此它的平方等于0 , 即
.
验证猜想1:
是a的算术平方根,因此它的平方等于a ,即
4
2
0
验证猜想1:
是4的算术平方根,因此它的平方等于4 , 即 ;…
1.双重非负性:
2.
二次根式性质:
验证猜想:
猜想2:
猜想1:
验证猜想:
猜想2:
二次根式性质2:
2
0.1
0
是一个非负数,它的平方等于 所以
是一个非负数,它的平方等于 所以
是一个非负数,它的平方等于 所以
是一个非负数,它的平方等于 ,所以
验证猜想2:
2
0.1
0
是一个非负数,它的平方等于
验证猜想2:
是一个非负数,它的平方等于 所以
验证猜想2:
不成立.
反例:
是一个非负数,它的平方等于 所以
2
0.1
2
0.1
0
是一个非负数,它的平方等于
验证猜想2:
是一个非负数,它的平方等于 所以
2
0.1
0
验证猜想2:
是一个非负数,它的平方等于 所以
2
0.1
0
是一个非负数,它的平方等于
验证猜想2:
是一个非负数,它的平方等于 所以
2
0.1
0
是一个非负数,它的平方等于 ,所以
验证猜想2:
是一个非负数,它的平方等于 所以
2
0.1
0
验证猜想2:
是一个非负数,它的平方等于 所以
1.双重非负性:
2.
3.
二次根式性质:
验证猜想:
二次根式性质2:
二次根式性质3:
性质
含义
a的取值
运算结果
a为任意实数
一个数的平方的算术平方根等于这个数的绝对值
一个非负数算术平方根的平方等于它本身
运用性质
例1 运用性质进行计算
(1)
运用 进行计算.
运用性质
(2)
例1 运用性质进行计算
运用 进行计算.
运用性质
(2)
例1 运用性质进行计算
运用 进行计算.
运用性质
若
, 则a的取值范围是( ).
(B)
(C)
(D)
(A)
D
法1:
法2:
例1 运用性质进行计算
(3)
运用性质
(1)判断下列等式是否成立:
例2 性质运用的辨析
运用性质
(2)对于题目:化简并求值:
其中 .
乙的解答如下:
甲的解答如下:
例2 性质运用的辨析
乙的解答:
甲的解答:
逆用性质
逆用性质
任意一个非负数都能写成平方的形式.
一个非负数算术平方根的平方等于它本身.
逆用性质
任意一个非负数都能化成二次根式的形式.
一个数的平方的算术平方根等于这个数的绝对值.
任意一个非负数都能化成平方的形式.
任意一个非负数都能化成二次根式的形式.
逆用性质
归纳小结
1. 二次根式的定义:
形如 (a≥0)的式子.
2. 二次根式的性质
(1)双重非负性:
(2)
(3)
作业
1.计算:
2.把下列非负数分别写成一个非负数的平方的形式:
3.一个圆柱体的高为10 ,体积为V.求它的底面半径r(用含V的
代数式表示),并分别求当V =5π , 10π和20π时 ,
底面半径r的大小.
祝同学们越来越优秀!
