4.3.3 利用边角边判定三角形全等课课练(含答案)
文档属性
| 名称 | 4.3.3 利用边角边判定三角形全等课课练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 22:09:53 | ||
图片预览

文档简介
北师大版数学七年级下册﹒同步课时训练
第四章 三角形
3 探索三角形全等的条件
第3课时 利用边角边判定三角形全等
一、选择题
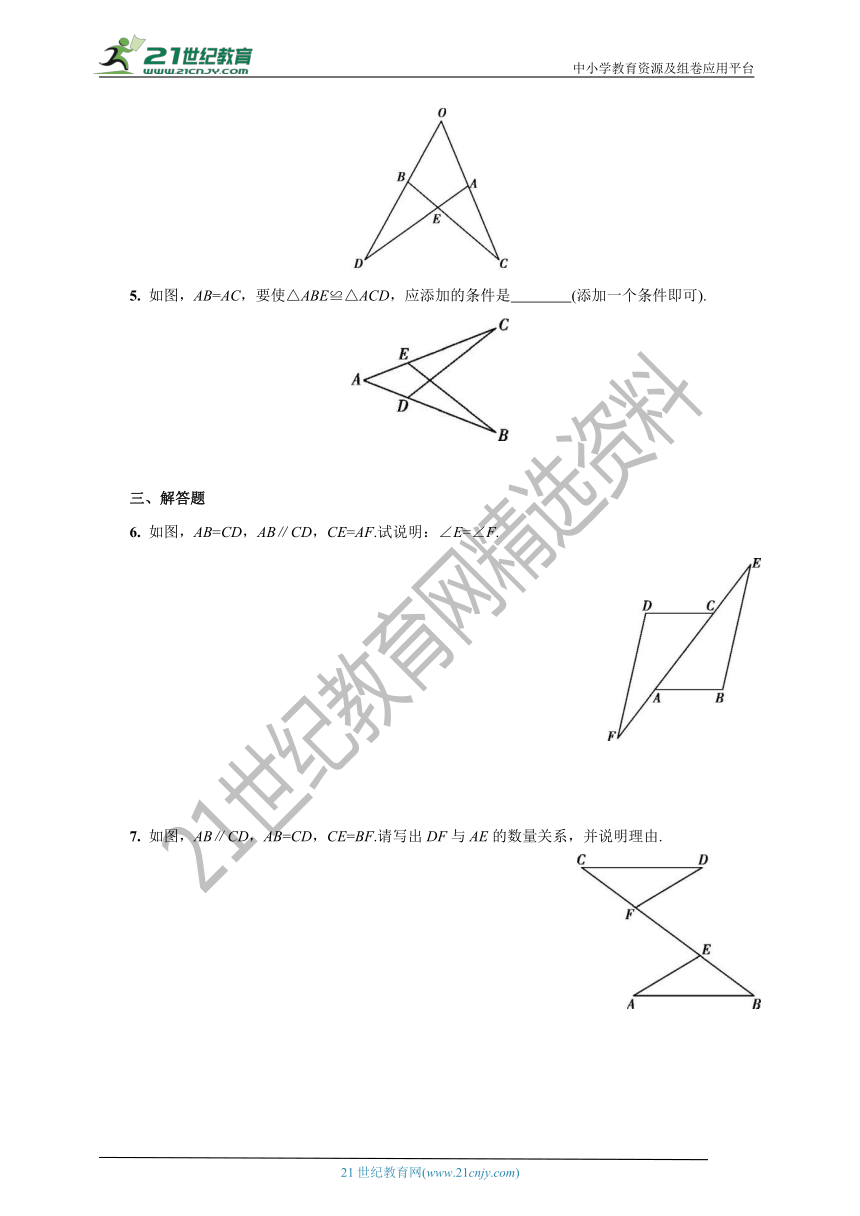
1. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,再添加以下的哪个条件仍不能判定△ABE≌△ACD的是( )
A. ∠B=∠C B. AD=AE C. BD=CE D. BE=CD
2. 如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为( )
A. 45 cm B. 48 cm C. 51 cm D. 54 cm
3. 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E的度数是( )
A. 25° B. 27° C. 30° D. 45°
二、填空题
4. 如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠OAD= 度. ?
5. 如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一个条件即可).?
三、解答题
6. 如图,AB=CD,AB∥CD,CE=AF.试说明:∠E=∠F.
7. 如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并说明理由.
8. 如图,已知AB=AD,AC=AE,∠BAE=∠DAC.试说明:∠C=∠E.
参 考 答 案
1. D 2. A 3. B
4. 95
5. ∠B=∠C(或AE=AD或∠AEB=∠ADC)
6. 解:∵CE=AF,∴AE=CF. ∵AB∥CD,∴∠DCA=∠CAB. 在△ABE与△CDF中,
∴△ABE≌△CDF(SAS),∴∠E=∠F.
7. 解:DF=AE. 理由:∵AB∥CD,∴∠C=∠B. ∵CE=BF,∴CE-EF=BF-FE,∴CF=BE. 又∵CD=AB,∴△DCF≌△ABE(SAS),∴DF=AE.
8. 解:∵∠BAE=∠DAC,∴∠BAE-∠CAE=∠DAC-∠CAE,即∠BAC=∠DAE,在△ABC和△ADE中,∵ ∴△ABC≌△ADE(SAS),∴∠C=∠E.
第四章 三角形
3 探索三角形全等的条件
第3课时 利用边角边判定三角形全等
一、选择题
1. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,再添加以下的哪个条件仍不能判定△ABE≌△ACD的是( )
A. ∠B=∠C B. AD=AE C. BD=CE D. BE=CD
2. 如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为( )
A. 45 cm B. 48 cm C. 51 cm D. 54 cm
3. 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E的度数是( )
A. 25° B. 27° C. 30° D. 45°
二、填空题
4. 如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠OAD= 度. ?
5. 如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 (添加一个条件即可).?
三、解答题
6. 如图,AB=CD,AB∥CD,CE=AF.试说明:∠E=∠F.
7. 如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并说明理由.
8. 如图,已知AB=AD,AC=AE,∠BAE=∠DAC.试说明:∠C=∠E.
参 考 答 案
1. D 2. A 3. B
4. 95
5. ∠B=∠C(或AE=AD或∠AEB=∠ADC)
6. 解:∵CE=AF,∴AE=CF. ∵AB∥CD,∴∠DCA=∠CAB. 在△ABE与△CDF中,
∴△ABE≌△CDF(SAS),∴∠E=∠F.
7. 解:DF=AE. 理由:∵AB∥CD,∴∠C=∠B. ∵CE=BF,∴CE-EF=BF-FE,∴CF=BE. 又∵CD=AB,∴△DCF≌△ABE(SAS),∴DF=AE.
8. 解:∵∠BAE=∠DAC,∴∠BAE-∠CAE=∠DAC-∠CAE,即∠BAC=∠DAE,在△ABC和△ADE中,∵ ∴△ABC≌△ADE(SAS),∴∠C=∠E.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
