4.3.2 利用角边角或角角边判定三角形全等课课练(含答案)
文档属性
| 名称 | 4.3.2 利用角边角或角角边判定三角形全等课课练(含答案) | 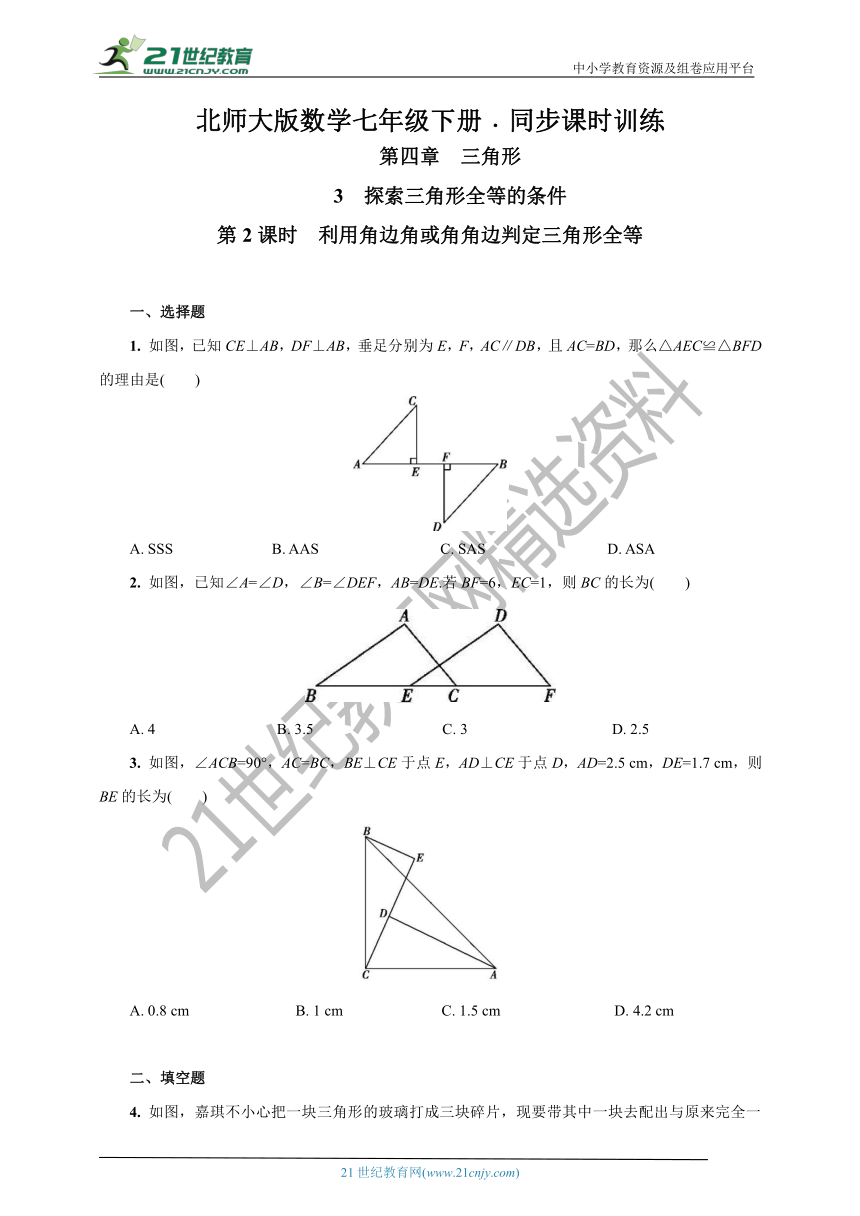 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 22:08:04 | ||
图片预览

文档简介
北师大版数学七年级下册﹒同步课时训练
第四章 三角形
3 探索三角形全等的条件
第2课时 利用角边角或角角边判定三角形全等
一、选择题
1. 如图,已知CE⊥AB,DF⊥AB,垂足分别为E,F,AC∥DB,且AC=BD,那么△AEC≌△BFD的理由是( )
A. SSS B. AAS C. SAS D. ASA
2. 如图,已知∠A=∠D,∠B=∠DEF,AB=DE.若BF=6,EC=1,则BC的长为( )
A. 4 B. 3.5 C. 3 D. 2.5
3. 如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,AD=2.5 cm,DE=1.7 cm,则BE的长为( )
A. 0.8 cm B. 1 cm C. 1.5 cm D. 4.2 cm
二、填空题
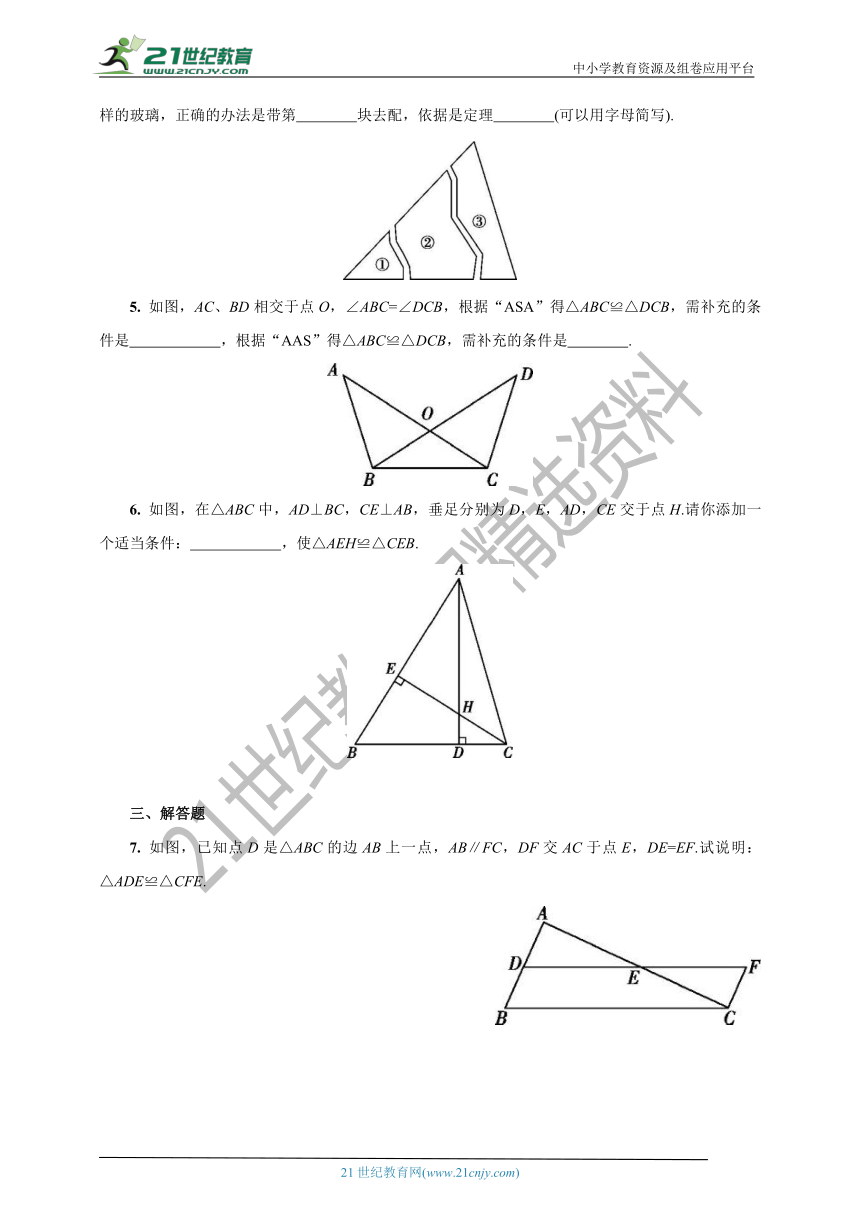
4. 如图,嘉琪不小心把一块三角形的玻璃打成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带第 块去配,依据是定理 (可以用字母简写).?
5. 如图,AC、BD相交于点O,∠ABC=∠DCB,根据“ASA”得△ABC≌△DCB,需补充的条件是 ,根据“AAS”得△ABC≌△DCB,需补充的条件是 .?
6. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H.请你添加一个适当条件: ,使△AEH≌△CEB.?
三、解答题
7. 如图,已知点D是△ABC的边AB上一点,AB∥FC,DF交AC于点E,DE=EF.试说明:△ADE≌△CFE.
8. 如图,在四边形ABCD中,E是AB的中点,AD∥EC,∠AED=∠B.
试说明:△AED≌△EBC.
参 考 答 案
1. B 2. B 3. A 4. ③ ASA
5. ∠ACB=∠DBC ∠A=∠D
6. AE=CE(或HE=BE或AH=CB或∠BAC=45°)
7. 解:解法一:∵AB∥FC,∴∠F=∠ADE. 在△ADE和△CFE中,有∴△ADE≌△CFE(ASA).
解法二:∵AB∥FC,∴∠A=∠ECF,在△ADE和△CFE中,有∴△ADE≌△CFE(AAS).
8. 解:∵AD∥EC,∴∠A=∠BEC. ∵E是AB的中点,∴AE=EB. ∵∠AED=∠B,∴△AED≌△EBC(ASA).
第四章 三角形
3 探索三角形全等的条件
第2课时 利用角边角或角角边判定三角形全等
一、选择题
1. 如图,已知CE⊥AB,DF⊥AB,垂足分别为E,F,AC∥DB,且AC=BD,那么△AEC≌△BFD的理由是( )
A. SSS B. AAS C. SAS D. ASA
2. 如图,已知∠A=∠D,∠B=∠DEF,AB=DE.若BF=6,EC=1,则BC的长为( )
A. 4 B. 3.5 C. 3 D. 2.5
3. 如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,AD=2.5 cm,DE=1.7 cm,则BE的长为( )
A. 0.8 cm B. 1 cm C. 1.5 cm D. 4.2 cm
二、填空题
4. 如图,嘉琪不小心把一块三角形的玻璃打成三块碎片,现要带其中一块去配出与原来完全一样的玻璃,正确的办法是带第 块去配,依据是定理 (可以用字母简写).?
5. 如图,AC、BD相交于点O,∠ABC=∠DCB,根据“ASA”得△ABC≌△DCB,需补充的条件是 ,根据“AAS”得△ABC≌△DCB,需补充的条件是 .?
6. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H.请你添加一个适当条件: ,使△AEH≌△CEB.?
三、解答题
7. 如图,已知点D是△ABC的边AB上一点,AB∥FC,DF交AC于点E,DE=EF.试说明:△ADE≌△CFE.
8. 如图,在四边形ABCD中,E是AB的中点,AD∥EC,∠AED=∠B.
试说明:△AED≌△EBC.
参 考 答 案
1. B 2. B 3. A 4. ③ ASA
5. ∠ACB=∠DBC ∠A=∠D
6. AE=CE(或HE=BE或AH=CB或∠BAC=45°)
7. 解:解法一:∵AB∥FC,∴∠F=∠ADE. 在△ADE和△CFE中,有∴△ADE≌△CFE(ASA).
解法二:∵AB∥FC,∴∠A=∠ECF,在△ADE和△CFE中,有∴△ADE≌△CFE(AAS).
8. 解:∵AD∥EC,∴∠A=∠BEC. ∵E是AB的中点,∴AE=EB. ∵∠AED=∠B,∴△AED≌△EBC(ASA).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
