人教版八年级数学 下册 第十八章 18.2.1 矩形 课时练(含答案)
文档属性
| 名称 | 人教版八年级数学 下册 第十八章 18.2.1 矩形 课时练(含答案) | 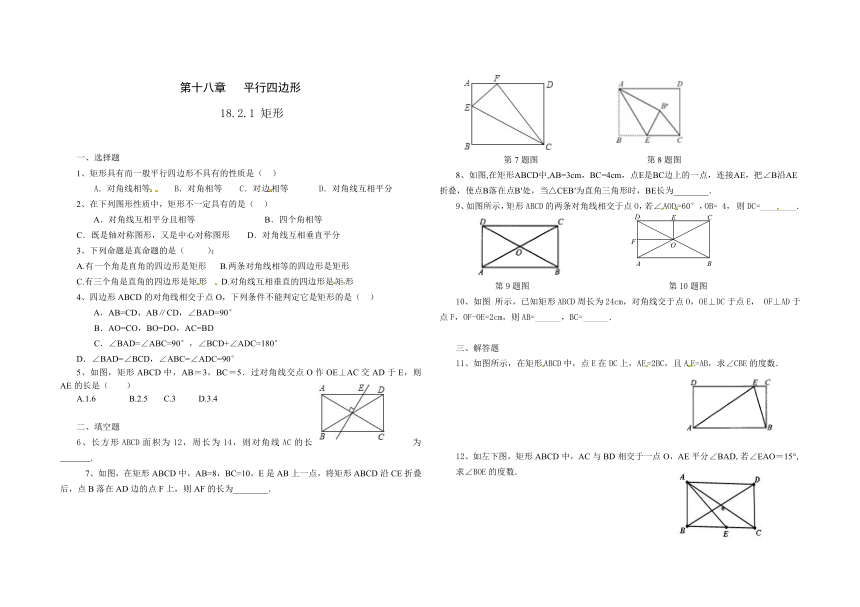 | |
| 格式 | zip | ||
| 文件大小 | 135.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 22:25:52 | ||
图片预览

文档简介
第十八章 平行四边形
18.2.1 矩形
一、选择题
1、矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对角相等 C.对边相等 D.对角线互相平分
2、在下列图形性质中,矩形不一定具有的是( )
A.对角线互相平分且相等 B.四个角相等
C.既是轴对称图形,又是中心对称图形 D.对角线互相垂直平分
3、下列命题是真命题的是( );
A.有一个角是直角的四边形是矩形 B.两条对角线相等的四边形是矩形
C.有三个角是直角的四边形是矩形 D.对角线互相垂直的四边形是矩形
4、四边形ABCD的对角线相交于点O,下列条件不能判定它是矩形的是( )
A.AB=CD,AB∥CD,∠BAD=90°
B.AO=CO,BO=DO,AC=BD
C.∠BAD=∠ABC=90°,∠BCD+∠ADC=180°
D.∠BAD=∠BCD,∠ABC=∠ADC=90°
5、如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是( )
A.1.6 B.2.5 C.3 D.3.4
填空题
6、长方形ABCD面积为12,周长为14,则对角线AC的长为 .
7、如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则AF的长为________.
第7题图 第8题图
8、如图,在矩形ABCD中,AB=3cm,BC=4cm,点E是BC边上的一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE长为________.
9、如图所示,矩形ABCD的两条对角线相交于点O,若∠AOD=60°,OB=4,则DC=________.
第9题图 第10题图
10、如图 所示,已知矩形ABCD周长为24cm,对角线交于点O,OE⊥DC于点E,OF⊥AD于点F,OF-OE=2cm,则AB=______,BC=______.
三、解答题
11、如图所示,在矩形ABCD中,点E在DC上,AE=2BC,且AE=AB,求∠CBE的度数.
12、如左下图,矩形ABCD中,AC与BD相交于一点O,AE平分∠BAD,若∠EAO=15°,
求∠BOE的度数.
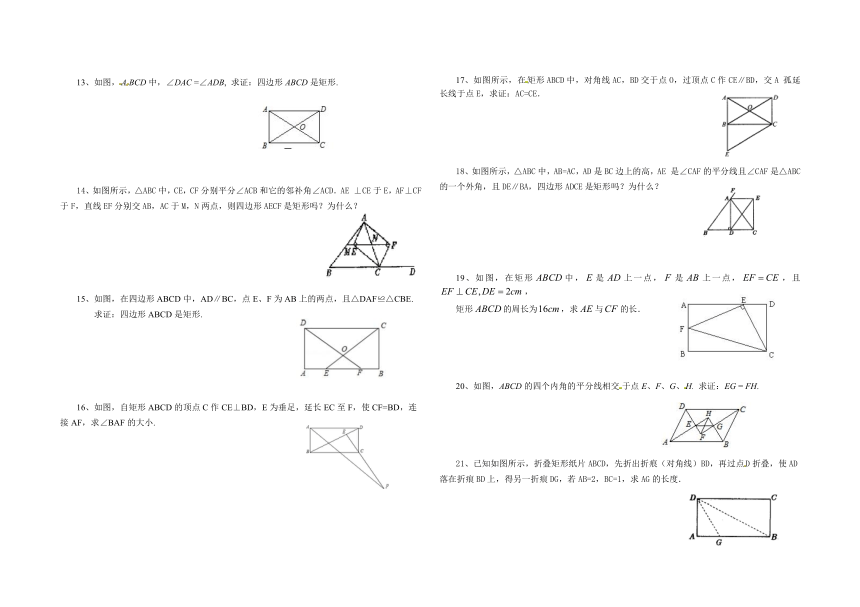
13、如图,ABCD中,∠DAC =∠ADB, 求证:四边形ABCD是矩形.
14、如图所示,△ABC中,CE,CF分别平分∠ACB和它的邻补角∠ACD.AE⊥CE于E,AF⊥CF于F,直线EF分别交AB,AC于M,N两点,则四边形AECF是矩形吗?为什么?
15、如图,在四边形ABCD中,AD∥BC,点E、F为AB上的两点,且△DAF≌△CBE.
求证:四边形ABCD是矩形.
16、如图,自矩形ABCD的顶点C作CE⊥BD,E为垂足,延长EC至F,使CF=BD,连接AF,求∠BAF的大小.
17、如图所示,在矩形ABCD中,对角线AC,BD交于点O,过顶点C作CE∥BD,交A孤延长线于点E,求证:AC=CE.
18、如图所示,△ABC中,AB=AC,AD是BC边上的高,AE是∠CAF的平分线且∠CAF是△ABC的一个外角,且DE∥BA,四边形ADCE是矩形吗?为什么?
19、如图,在矩形中,是上一点,是上一点,,且,
矩形的周长为,求与的长.
20、如图,ABCD的四个内角的平分线相交于点E、F、G、H. 求证:EG = FH.
21、已知如图所示,折叠矩形纸片ABCD,先折出折痕(对角线)BD,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,求AG的长度.
参考答案:
一、1、A 2、D 3、C 4、C 5、D
二、6、5
7、4
8、3或1.5
9、4
10、8cm ,4cm
三、11、15°
∠BOE=
提示:证明AC = BD
14、解:四边形AECF是矩形.∠ECF=(∠ACB+∠ACD)=90°.∠AEC=∠AFC=90°,
点拨:本题是通过证四边形中三个角为直角得出结论.还可以通过证其为平行四边形,再证有一个角为直角得出结论.
15、【提示】
由△DAF≌△CBE可知AD=BC,所以四边形ABCD是平行四边形;
再根据∠A=∠B,且∠A+∠B=180°,所以∠A=∠B=90°;
综上所述,四边形ABCD是矩形.
16、解:如图,连接AC,则AC=BD=CF,
所以∠F=∠5,而且∠1=∠3
∠4=∠6-∠7=∠BEF+∠F-∠7
=90°-∠7+∠F
=∠1+∠F
=∠3+∠5
=∠2
∴∠4=∠2= =45°,
∴∠BAF的度数为45°。
17、证四边形BDCE是平行四边形,得CE=BD=AC
18、解:是矩形;理由:∠CAE=∠ACB,所以AE∥BC.又DE∥BA,所以四边形ABDE是平行四边形,所以AE=BD,所以AE=DC.又因为AE∥DC,所以四边形ADCE是平行四边形.又因为∠ADC=90°,所以四边形ADCE是矩形.
19、【答案】 ,
20、提示:证四边形EFGH是矩形.
21、解:如图所示,过点G作GE⊥BD于点E, 则AG=EG,AD=ED.在Rt△ABD中,由勾股定理,得BD=,所以BE=BD-DE=BD-AD=-1,BG=AB-AG=2-AG,设AG=EG=x,则BG=2-x.在Rt△BEG中,由勾股定理,得BG2=EG2+BE2,即(2-x)2=(-1)2+x2,
解得x=,即AG=.
18.2.1 矩形
一、选择题
1、矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对角相等 C.对边相等 D.对角线互相平分
2、在下列图形性质中,矩形不一定具有的是( )
A.对角线互相平分且相等 B.四个角相等
C.既是轴对称图形,又是中心对称图形 D.对角线互相垂直平分
3、下列命题是真命题的是( );
A.有一个角是直角的四边形是矩形 B.两条对角线相等的四边形是矩形
C.有三个角是直角的四边形是矩形 D.对角线互相垂直的四边形是矩形
4、四边形ABCD的对角线相交于点O,下列条件不能判定它是矩形的是( )
A.AB=CD,AB∥CD,∠BAD=90°
B.AO=CO,BO=DO,AC=BD
C.∠BAD=∠ABC=90°,∠BCD+∠ADC=180°
D.∠BAD=∠BCD,∠ABC=∠ADC=90°
5、如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是( )
A.1.6 B.2.5 C.3 D.3.4
填空题
6、长方形ABCD面积为12,周长为14,则对角线AC的长为 .
7、如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的点F上,则AF的长为________.
第7题图 第8题图
8、如图,在矩形ABCD中,AB=3cm,BC=4cm,点E是BC边上的一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE长为________.
9、如图所示,矩形ABCD的两条对角线相交于点O,若∠AOD=60°,OB=4,则DC=________.
第9题图 第10题图
10、如图 所示,已知矩形ABCD周长为24cm,对角线交于点O,OE⊥DC于点E,OF⊥AD于点F,OF-OE=2cm,则AB=______,BC=______.
三、解答题
11、如图所示,在矩形ABCD中,点E在DC上,AE=2BC,且AE=AB,求∠CBE的度数.
12、如左下图,矩形ABCD中,AC与BD相交于一点O,AE平分∠BAD,若∠EAO=15°,
求∠BOE的度数.
13、如图,ABCD中,∠DAC =∠ADB, 求证:四边形ABCD是矩形.
14、如图所示,△ABC中,CE,CF分别平分∠ACB和它的邻补角∠ACD.AE⊥CE于E,AF⊥CF于F,直线EF分别交AB,AC于M,N两点,则四边形AECF是矩形吗?为什么?
15、如图,在四边形ABCD中,AD∥BC,点E、F为AB上的两点,且△DAF≌△CBE.
求证:四边形ABCD是矩形.
16、如图,自矩形ABCD的顶点C作CE⊥BD,E为垂足,延长EC至F,使CF=BD,连接AF,求∠BAF的大小.
17、如图所示,在矩形ABCD中,对角线AC,BD交于点O,过顶点C作CE∥BD,交A孤延长线于点E,求证:AC=CE.
18、如图所示,△ABC中,AB=AC,AD是BC边上的高,AE是∠CAF的平分线且∠CAF是△ABC的一个外角,且DE∥BA,四边形ADCE是矩形吗?为什么?
19、如图,在矩形中,是上一点,是上一点,,且,
矩形的周长为,求与的长.
20、如图,ABCD的四个内角的平分线相交于点E、F、G、H. 求证:EG = FH.
21、已知如图所示,折叠矩形纸片ABCD,先折出折痕(对角线)BD,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,求AG的长度.
参考答案:
一、1、A 2、D 3、C 4、C 5、D
二、6、5
7、4
8、3或1.5
9、4
10、8cm ,4cm
三、11、15°
∠BOE=
提示:证明AC = BD
14、解:四边形AECF是矩形.∠ECF=(∠ACB+∠ACD)=90°.∠AEC=∠AFC=90°,
点拨:本题是通过证四边形中三个角为直角得出结论.还可以通过证其为平行四边形,再证有一个角为直角得出结论.
15、【提示】
由△DAF≌△CBE可知AD=BC,所以四边形ABCD是平行四边形;
再根据∠A=∠B,且∠A+∠B=180°,所以∠A=∠B=90°;
综上所述,四边形ABCD是矩形.
16、解:如图,连接AC,则AC=BD=CF,
所以∠F=∠5,而且∠1=∠3
∠4=∠6-∠7=∠BEF+∠F-∠7
=90°-∠7+∠F
=∠1+∠F
=∠3+∠5
=∠2
∴∠4=∠2= =45°,
∴∠BAF的度数为45°。
17、证四边形BDCE是平行四边形,得CE=BD=AC
18、解:是矩形;理由:∠CAE=∠ACB,所以AE∥BC.又DE∥BA,所以四边形ABDE是平行四边形,所以AE=BD,所以AE=DC.又因为AE∥DC,所以四边形ADCE是平行四边形.又因为∠ADC=90°,所以四边形ADCE是矩形.
19、【答案】 ,
20、提示:证四边形EFGH是矩形.
21、解:如图所示,过点G作GE⊥BD于点E, 则AG=EG,AD=ED.在Rt△ABD中,由勾股定理,得BD=,所以BE=BD-DE=BD-AD=-1,BG=AB-AG=2-AG,设AG=EG=x,则BG=2-x.在Rt△BEG中,由勾股定理,得BG2=EG2+BE2,即(2-x)2=(-1)2+x2,
解得x=,即AG=.
