青岛版七年级数学下册 11.6零次幂和负整数指数幂课件(共21张PPT)
文档属性
| 名称 | 青岛版七年级数学下册 11.6零次幂和负整数指数幂课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 23:14:14 | ||
图片预览







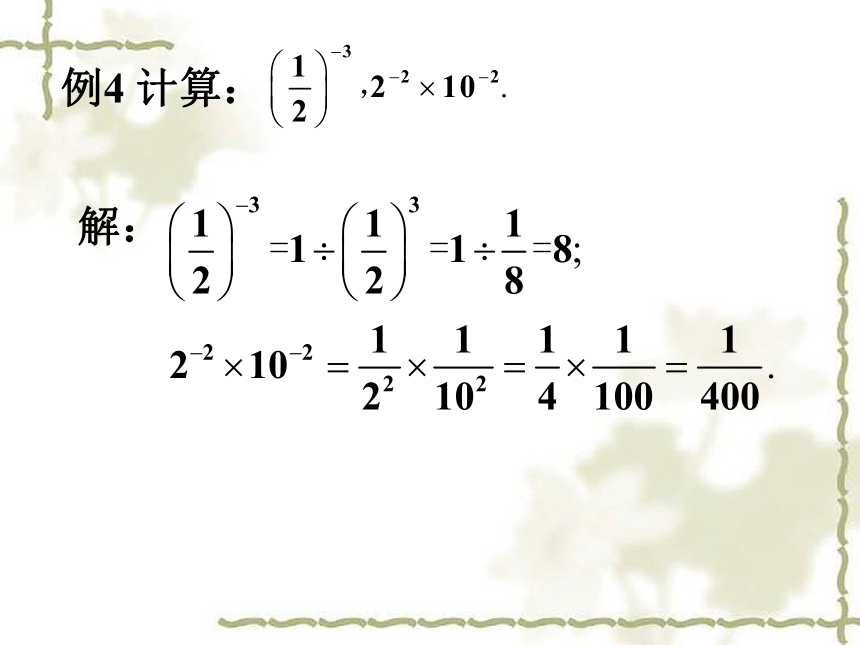

文档简介
(共21张PPT)
11.6零指数幂与负整数指数幂
复
习
正整数指数幂有哪些运算性质?
新课
1、计算
(1)52÷ 52=
(2)103 ÷103=
(3)a5 ÷a5= (a≠0)
52-2=50
103-3=100
a5-5=a0
规定:50=1 100=1 a0=1 (a≠0)
任何不等于零的数的零次幂都等于1
利用同底数幂的除法公式,结果如何呢?
1
1
1
例1 计算:
解:
例2 计算:
解:
am÷an=am-n (a≠0 m、n为正整数且m>n)
a5÷a3=a2
a3÷a5=?
分
析
a3÷a5=a3-5=a-2
a3÷a5=
=
n是正整数时,a-n属于分式.并且
(a≠0)
例如:
引入负整数指数幂后,指数的取值范围就扩大到全体整数.
am=
am (m是正整数)
1 (m=0)
(m是负整数)
即:a-n(a≠0)是an的倒数
例3 计算:
解:
例4 计算:
解:
(1)32=_____, 30=___, 3-2=_____;
(2)(-3)2=____,(-3)0=___,(-3)-2=_____;
(3)b2=_____,b0=____,b-2=____(b≠0).
练
习
指数从正整数推广到了整数,正整数指数幂的各种运算法则对整数指数幂都适用.
例6 计算:
解:
n
n
(n为正整数)
用小数表示
练习:用小数表示
n个0
n的值:有效数字前所有零的个数(包括小数点前的零)
(1) 0.005
= 5 × 0.001
= 5 × 10-3
(2) 0.020 4
= 2.04 × 0.01
= 2.04 × 10-2
(3) 0.000 36
= 3.6 × 0.000 1
= 3.6 × 10-4
用科学记数法表示下列各数:
例8 已知某花粉直径为360000纳米,用科学计数法表示,该花粉的直径是多少米?
解:
1.计算:
(1)(-0.1)0;
(4) 2-2 ;
.
(3)
(2)
2.用科学记数法填空:
(1)1秒是1微秒的1000000倍,则1微秒=________秒;
(2)1毫克=_________千克;
(3)1微米=_________米;
(4)1纳米=_________微米;
(5)1平方厘米=_________平方米;
(6)1毫升=_________立方米.
1
1
4
0.25
(1)0.000 03; (2)-0.000 0064;
(3)0.000 0314; (4)2013 000.
4.计算下列各式,并且把结果化为只含有正整指数幂的形式:
3.用科学记数法表示:
这节课我们学了什么?
11.6零指数幂与负整数指数幂
复
习
正整数指数幂有哪些运算性质?
新课
1、计算
(1)52÷ 52=
(2)103 ÷103=
(3)a5 ÷a5= (a≠0)
52-2=50
103-3=100
a5-5=a0
规定:50=1 100=1 a0=1 (a≠0)
任何不等于零的数的零次幂都等于1
利用同底数幂的除法公式,结果如何呢?
1
1
1
例1 计算:
解:
例2 计算:
解:
am÷an=am-n (a≠0 m、n为正整数且m>n)
a5÷a3=a2
a3÷a5=?
分
析
a3÷a5=a3-5=a-2
a3÷a5=
=
n是正整数时,a-n属于分式.并且
(a≠0)
例如:
引入负整数指数幂后,指数的取值范围就扩大到全体整数.
am=
am (m是正整数)
1 (m=0)
(m是负整数)
即:a-n(a≠0)是an的倒数
例3 计算:
解:
例4 计算:
解:
(1)32=_____, 30=___, 3-2=_____;
(2)(-3)2=____,(-3)0=___,(-3)-2=_____;
(3)b2=_____,b0=____,b-2=____(b≠0).
练
习
指数从正整数推广到了整数,正整数指数幂的各种运算法则对整数指数幂都适用.
例6 计算:
解:
n
n
(n为正整数)
用小数表示
练习:用小数表示
n个0
n的值:有效数字前所有零的个数(包括小数点前的零)
(1) 0.005
= 5 × 0.001
= 5 × 10-3
(2) 0.020 4
= 2.04 × 0.01
= 2.04 × 10-2
(3) 0.000 36
= 3.6 × 0.000 1
= 3.6 × 10-4
用科学记数法表示下列各数:
例8 已知某花粉直径为360000纳米,用科学计数法表示,该花粉的直径是多少米?
解:
1.计算:
(1)(-0.1)0;
(4) 2-2 ;
.
(3)
(2)
2.用科学记数法填空:
(1)1秒是1微秒的1000000倍,则1微秒=________秒;
(2)1毫克=_________千克;
(3)1微米=_________米;
(4)1纳米=_________微米;
(5)1平方厘米=_________平方米;
(6)1毫升=_________立方米.
1
1
4
0.25
(1)0.000 03; (2)-0.000 0064;
(3)0.000 0314; (4)2013 000.
4.计算下列各式,并且把结果化为只含有正整指数幂的形式:
3.用科学记数法表示:
这节课我们学了什么?
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
