北京版七年级数学下册4.1 不等式的概念 课件 (37张PPT)
文档属性
| 名称 | 北京版七年级数学下册4.1 不等式的概念 课件 (37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
七年级下册 数学
不等式的概念
生活中的不等关系
(1)妈妈每天起床的时间在6点之前;
(2)太阳的体积比地球大;
(3)哥哥与弟弟的身高不相等.
(1)妈妈每天起床的时间在6点之前;
如果用x表示妈妈每天起床的时间,那么就可表示为
x<6.
生活中的不等关系
(2)太阳的体积比地球大;
如果用a,b分别表示太阳、地球的体积,
那么就可表示为
a>b.
生活中的不等关系
(3)哥哥与弟弟的身高不相等.
m ≠ n.
如果用m 和 n分别表示哥哥与弟弟的身高,
那么就可表示为
生活中的不等关系
数学中的不等关系
55>20, 4>-1, 0<6 ,
-1>-2, 5-9<3+7.
数学中的不等关系
a<0, b>0,a<b,或写成 b>a.
数轴上右边的点表示的数
总比左边的点表示的数大
归纳概括
4>-1, 5-9 < 3+7, x < 6,a>b,
m≠n,a < 0,b>0,a < b,像这样的式子叫不等式.
回顾旧知
用“=”表示相等关系的式子叫做等式
等式
不等式
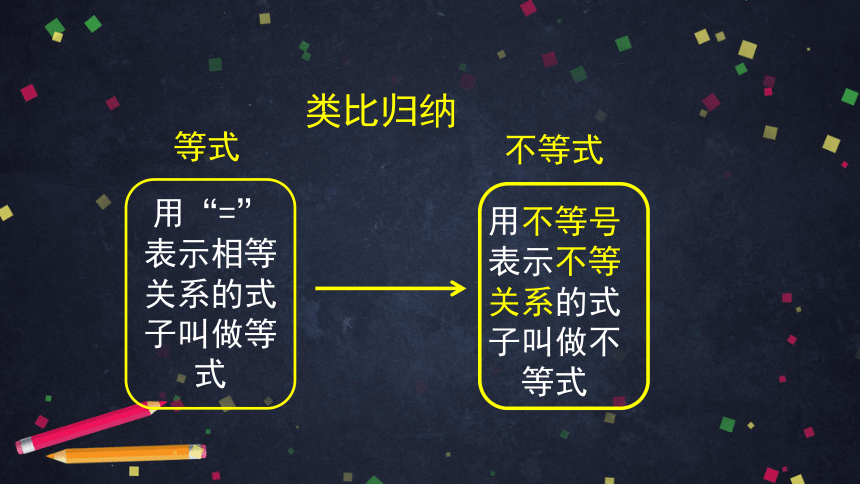
类比归纳
用“=”表示相等关系的式子叫做等式
等式
不等式
用不等号表示不等关系的式子叫做不等式
类比归纳
用“=”表示相等关系的式子叫做等式
等式
不等式
用不等号表示不等关系的式子叫做不等式
探索
在电脑前连续工作不宜超过1小时.怎样用不等式表示呢?
如果用t 表示在电脑前连续工作的时间,那么t 与1之间
的关系是
t <1
或t =1.
探索
在电脑前连续工作不宜超过1小时.怎样用不等式表示呢?
t<1或t =1.
把“<”和“=”结合起来使用,写成“≤”,
读作“小于或等于”,也就是“不大于”.
所以不等式表示为 t≤1.
探索
小红每月的生活费不少于1000元,怎样用不等式表示呢?
“不少于”的含义是“不小于”,也就是“大于或
等于”,用符号“≥”表示.
如果用x表示小红每月的生活费,那么x与1000的关系是:
x>1000
x≥1000.
或x =1000.
归纳:
用符号“≥”或“≤”连接起来的式子也叫做不等式.
表示不等关系的符号有“ >”,“<”,“≠”,“≥”,“≤”.
再探索
红圈表示“不超过”,
蓝底白字表示“不低于”.
用v表示小轿车时速,
表示为:v≤100,
v≥60.
再探索
红圈表示“不超过”,
蓝底白字表示“不低于”.
v≥60写成60≤v.
表示为: 60≤v≤100.
例题讲解
例1 用不等式表示下面的不等关系:
(1)张平的年龄比杨洋大;
(2)某种电梯标明“载客不超过13人”;
(3)北京某一天的最低气温是-3℃,最高气温是12 ℃ .
例题讲解
例1 用不等式表示下面的不等关系:
(1)张平的年龄比杨洋大;
分析:张平的年龄和杨洋的年龄,不等关系是大于.
解:设张平的年龄为a ,杨洋的年龄为b.
张平的年龄比杨洋大,用不等式表示为
a>b.
例1 用不等式表示下面的不等关系:
(2)某种电梯标明“载客不超过13人”;
分析:不等关系是“不超过”,也就是小于或等于.
解:设乘坐电梯的人数为 x 人,载客不超过13人,
用不等式表示为 x ≤13.
例题讲解
例1 用不等式表示下面的不等关系:
(3)北京某一天的最低气温是-3 ℃ ,最高气温是12 ℃ .
分析:最低气温是-3 ℃,也就是温度大于或等于-3 ℃ .
最高气温是12 ℃,也就是温度小于或等于12 ℃.
x≥-3,
x≤12
-3≤x≤12
例题讲解
例1 用不等式表示下面的不等关系:
(3)北京某一天的最低气温是-3 ℃ ,最高气温是12 ℃.
解:设北京某一天的气温为 x ℃ .
最低气温是-3 ℃ ,最高气温是12 ℃ ,用不等式表示为
-3≤x≤12.
例题讲解
总结积累
量的表示
理解关键词
列不等式
例题讲解
例2 用不等式表示下列关系:
(1)a与b的和大于3; (2)x与6的差是负数;
(3)x的5倍不小于20; (4)m 与7的和是非正数;
(5)2x 与4的差是非负数.
例题讲解
例2 用不等式表示下列关系:
(1)a与b的和大于3;
a + b
分析:两个量:a与b的和,3.
关键词:大于
3
>
.
解:
例题讲解
分析:x与6的差表示为x-6 ,负数是小于0的数.
解: x-6<0.
例2 用不等式表示下列关系:
(2) x与6的差是负数;
例题讲解
分析: 关键词:不小于,也就是大于或等于.
解: 5x≥ 20.
用符号“≥”连接.
例2 用不等式表示下列关系:
(3)x的5倍不小于20;
例题讲解
分析:
非正数是指不是正数的数,也就是负数或零,
比较m +7与 0 的大小,用“≤” 连接.
解: m+7≤ 0.
例2 用不等式表示下列关系:
(4) m与7的和是非正数;
例题讲解
分析:
非负数是指不是负数的数,也就是正数或零,
比较2x -4与0的大小,用符号“≥” 连接.
.
解: 2x-4 ≥ 0.
例2 用不等式表示下列关系:
(5) 2x与4的差是非负数.
总结积累
关键词语:大于 小于 不大于 不小于
超过 低于 不超过 不低于
比……大 比……小 不多于 不少于
符号: > < ≤
≥
总结积累
如果用a 表示一个数(或者一个量).
关键词语:a是正数 a是负数 a是非正数 a是非负数
表示为: a > 0 a < 0 a ≤ 0 a ≥ 0
巩固提高
1.用不等式表示下列关系:
(1)哥哥存款x元,弟弟存款y元,兄弟二人的存款总 数少于1000元;
x + y <1000.
(2)今年父亲的年龄是40岁,儿子的年龄是13岁,x年 后父亲的年龄与儿子的年龄的关系.
40+x > 13+x.
巩固提高
2.用不等式表示:
(1)a是正数;
(2)x与8的和小于6;
(3)y的相反数大于或等于5;
(4)2m与3n的差是非负数.
a>0
x + 8<6
-y ≥5
2m - 3n≥0
回顾小结
表示
不等关系
不等式
刻画
不等号
不等关系
解决
已有方法
新的问题
布置作业
1.根据下列数量关系,列出不等式:
(1)5x与4的和是负数;
(2)x 小于它的相反数;
(3)y 的四分之一与x的三分之一的和不大于0;
(4)m的3 倍大于或等于10 ;
(5)2a与3b的差是非负数.
2. 用不等式表示下列不等关系:
(1)学生甲的身高是a 厘米,学生乙的身高是b厘米,
甲与乙身高的差是正数.
(2)姐姐每月上网20小时,妹妹每月上网x小时,妹
妹每月上网的时间超过了姐姐上网时间的2倍.
(3)小明家每月的电话费m元在150元以内
(不含150元).
.
布置作业
3.写个人学习感想:哪个知识最重要,最有用
,需要注意的关键之处等.
七年级下册 数学
不等式的概念
生活中的不等关系
(1)妈妈每天起床的时间在6点之前;
(2)太阳的体积比地球大;
(3)哥哥与弟弟的身高不相等.
(1)妈妈每天起床的时间在6点之前;
如果用x表示妈妈每天起床的时间,那么就可表示为
x<6.
生活中的不等关系
(2)太阳的体积比地球大;
如果用a,b分别表示太阳、地球的体积,
那么就可表示为
a>b.
生活中的不等关系
(3)哥哥与弟弟的身高不相等.
m ≠ n.
如果用m 和 n分别表示哥哥与弟弟的身高,
那么就可表示为
生活中的不等关系
数学中的不等关系
55>20, 4>-1, 0<6 ,
-1>-2, 5-9<3+7.
数学中的不等关系
a<0, b>0,a<b,或写成 b>a.
数轴上右边的点表示的数
总比左边的点表示的数大
归纳概括
4>-1, 5-9 < 3+7, x < 6,a>b,
m≠n,a < 0,b>0,a < b,像这样的式子叫不等式.
回顾旧知
用“=”表示相等关系的式子叫做等式
等式
不等式
类比归纳
用“=”表示相等关系的式子叫做等式
等式
不等式
用不等号表示不等关系的式子叫做不等式
类比归纳
用“=”表示相等关系的式子叫做等式
等式
不等式
用不等号表示不等关系的式子叫做不等式
探索
在电脑前连续工作不宜超过1小时.怎样用不等式表示呢?
如果用t 表示在电脑前连续工作的时间,那么t 与1之间
的关系是
t <1
或t =1.
探索
在电脑前连续工作不宜超过1小时.怎样用不等式表示呢?
t<1或t =1.
把“<”和“=”结合起来使用,写成“≤”,
读作“小于或等于”,也就是“不大于”.
所以不等式表示为 t≤1.
探索
小红每月的生活费不少于1000元,怎样用不等式表示呢?
“不少于”的含义是“不小于”,也就是“大于或
等于”,用符号“≥”表示.
如果用x表示小红每月的生活费,那么x与1000的关系是:
x>1000
x≥1000.
或x =1000.
归纳:
用符号“≥”或“≤”连接起来的式子也叫做不等式.
表示不等关系的符号有“ >”,“<”,“≠”,“≥”,“≤”.
再探索
红圈表示“不超过”,
蓝底白字表示“不低于”.
用v表示小轿车时速,
表示为:v≤100,
v≥60.
再探索
红圈表示“不超过”,
蓝底白字表示“不低于”.
v≥60写成60≤v.
表示为: 60≤v≤100.
例题讲解
例1 用不等式表示下面的不等关系:
(1)张平的年龄比杨洋大;
(2)某种电梯标明“载客不超过13人”;
(3)北京某一天的最低气温是-3℃,最高气温是12 ℃ .
例题讲解
例1 用不等式表示下面的不等关系:
(1)张平的年龄比杨洋大;
分析:张平的年龄和杨洋的年龄,不等关系是大于.
解:设张平的年龄为a ,杨洋的年龄为b.
张平的年龄比杨洋大,用不等式表示为
a>b.
例1 用不等式表示下面的不等关系:
(2)某种电梯标明“载客不超过13人”;
分析:不等关系是“不超过”,也就是小于或等于.
解:设乘坐电梯的人数为 x 人,载客不超过13人,
用不等式表示为 x ≤13.
例题讲解
例1 用不等式表示下面的不等关系:
(3)北京某一天的最低气温是-3 ℃ ,最高气温是12 ℃ .
分析:最低气温是-3 ℃,也就是温度大于或等于-3 ℃ .
最高气温是12 ℃,也就是温度小于或等于12 ℃.
x≥-3,
x≤12
-3≤x≤12
例题讲解
例1 用不等式表示下面的不等关系:
(3)北京某一天的最低气温是-3 ℃ ,最高气温是12 ℃.
解:设北京某一天的气温为 x ℃ .
最低气温是-3 ℃ ,最高气温是12 ℃ ,用不等式表示为
-3≤x≤12.
例题讲解
总结积累
量的表示
理解关键词
列不等式
例题讲解
例2 用不等式表示下列关系:
(1)a与b的和大于3; (2)x与6的差是负数;
(3)x的5倍不小于20; (4)m 与7的和是非正数;
(5)2x 与4的差是非负数.
例题讲解
例2 用不等式表示下列关系:
(1)a与b的和大于3;
a + b
分析:两个量:a与b的和,3.
关键词:大于
3
>
.
解:
例题讲解
分析:x与6的差表示为x-6 ,负数是小于0的数.
解: x-6<0.
例2 用不等式表示下列关系:
(2) x与6的差是负数;
例题讲解
分析: 关键词:不小于,也就是大于或等于.
解: 5x≥ 20.
用符号“≥”连接.
例2 用不等式表示下列关系:
(3)x的5倍不小于20;
例题讲解
分析:
非正数是指不是正数的数,也就是负数或零,
比较m +7与 0 的大小,用“≤” 连接.
解: m+7≤ 0.
例2 用不等式表示下列关系:
(4) m与7的和是非正数;
例题讲解
分析:
非负数是指不是负数的数,也就是正数或零,
比较2x -4与0的大小,用符号“≥” 连接.
.
解: 2x-4 ≥ 0.
例2 用不等式表示下列关系:
(5) 2x与4的差是非负数.
总结积累
关键词语:大于 小于 不大于 不小于
超过 低于 不超过 不低于
比……大 比……小 不多于 不少于
符号: > < ≤
≥
总结积累
如果用a 表示一个数(或者一个量).
关键词语:a是正数 a是负数 a是非正数 a是非负数
表示为: a > 0 a < 0 a ≤ 0 a ≥ 0
巩固提高
1.用不等式表示下列关系:
(1)哥哥存款x元,弟弟存款y元,兄弟二人的存款总 数少于1000元;
x + y <1000.
(2)今年父亲的年龄是40岁,儿子的年龄是13岁,x年 后父亲的年龄与儿子的年龄的关系.
40+x > 13+x.
巩固提高
2.用不等式表示:
(1)a是正数;
(2)x与8的和小于6;
(3)y的相反数大于或等于5;
(4)2m与3n的差是非负数.
a>0
x + 8<6
-y ≥5
2m - 3n≥0
回顾小结
表示
不等关系
不等式
刻画
不等号
不等关系
解决
已有方法
新的问题
布置作业
1.根据下列数量关系,列出不等式:
(1)5x与4的和是负数;
(2)x 小于它的相反数;
(3)y 的四分之一与x的三分之一的和不大于0;
(4)m的3 倍大于或等于10 ;
(5)2a与3b的差是非负数.
2. 用不等式表示下列不等关系:
(1)学生甲的身高是a 厘米,学生乙的身高是b厘米,
甲与乙身高的差是正数.
(2)姐姐每月上网20小时,妹妹每月上网x小时,妹
妹每月上网的时间超过了姐姐上网时间的2倍.
(3)小明家每月的电话费m元在150元以内
(不含150元).
.
布置作业
3.写个人学习感想:哪个知识最重要,最有用
,需要注意的关键之处等.
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
