人教版八年级数学 下册 第十七章 17.2 勾股定理的逆定理 课时练(含答案)
文档属性
| 名称 | 人教版八年级数学 下册 第十七章 17.2 勾股定理的逆定理 课时练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 76.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-01 22:36:32 | ||
图片预览

文档简介
第十七章 勾股定理
17.2 勾股定理的逆定理
一、选择题
1、下列定理中,有逆定理的个数是( )
①有两边相等的三角形是等腰三角形;②若三角形的三边长a,b,c满足a2+b2=c2,则该三角形是直角三角形;③全等三角形的对应角相等;④若a=b, a2 =b2.
A. 1个 B. 2个 C. 3个 D. 4个
2、在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A-∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2-c2,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形
D.如果a2:b2:c2=9:16:25,那么△ABC是直角三角形
3、下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6
C.5,12,13 D.4,6,7
4、一个三角形的三边的长分别是3,4,5,则这个三角形最长边上的高是 ( )
A.4 B.3 C.2.5 D.2.4
5、下列命题的逆命题是真命题的是 ( )
A.若a=b,则|a|=|b|
B.全等三角形的周长相等
C.若a=0,则ab=0
D.有两边相等的三角形是等腰三角形
填空题
6、在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做____________;如果把其中一个命题叫做原命题,那么另一个命题叫做它的____________.
7、一个三角形三条边的比为5:12:13,且周长为60cm,则它的面积是
8、 已知两条线段长分别为3,4,那么能与它们组成直角三角形的第三条线段长是
9、已知△ ABC中,BC=41,AC=40,AB=9,则此三角形为 三角形, 是最大角.
10、已知△ABC的三边a,b,c满足(a-5)2+(b-12)2+|c-13|=0,则△ABC是__________三角形.
三、解答题
11、写出下列命题的逆命题,并判断这些逆命题是否成立.
(1) 如果a=0,那么 ab=0;
(2) 如果x=4,那么x2=16;
(3) 面积相等的三角形是全等三角形;
(4) 如果三角形有一个内角是钝角,那么其余两个角是锐角;
(5) 在一个三角形中,等角对等边.
12、如图所示,在四边形ABCD中,AB=2,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积。
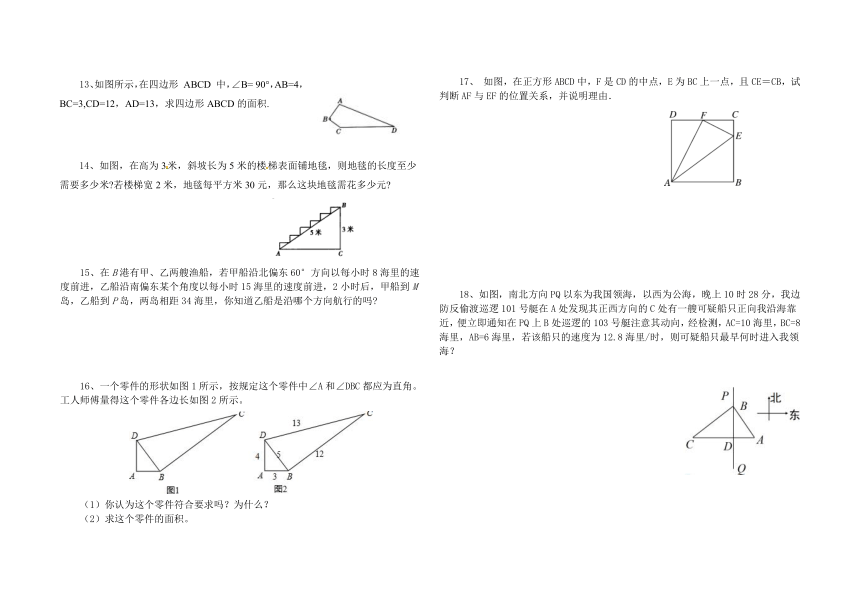
13、如图所示,在四边形 ABCD 中,∠B= 90°,AB=4,BC=3,CD=12,AD=13,求四边形ABCD的面积.
14、如图,在高为3米,斜坡长为5米的楼梯表面铺地毯,则地毯的长度至少需要多少米?若楼梯宽2米,地毯每平方米30元,那么这块地毯需花多少元?
15、在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里的速度前进,乙船沿南偏东某个角度以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?
16、一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边长如图2所示。
(1)你认为这个零件符合要求吗?为什么?
(2)求这个零件的面积。
17、 如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
18、如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
参考答案:
一、1、B 解析 ①的逆命题是“等腰三角形有两边相等”,是真命题;②的逆命题是“若直角三角形的两条直角边长分别为a,b,斜边长为c,则三边长a,b,c满足a2+b2=c2”,是真命题;③对应角相等的两个三角形不一定全等;④若a2=b2,则a与b不一定相等,所以③④的逆命题是假命题,没有逆等理.
2、B【答案】B
【解析】如果∠A-∠B=∠C,那么△ABC是直角三角形,A正确;如果a2=b2-c2,那么△ABC是直角三角形且∠B=90°,B错误;如果∠A:∠B:∠C=1:3:2,设∠A=x,则∠B=2x,∠C=3x,则x+3x+2x=180°,解得,x=30°,则3x=90°,那么△ABC是直角三角形,C正确;如果a2:b2:c2=9:16:25,则如果a2+b2=c2,那么△ABC是直角三角形,D正确;故选:B。
C
D
【解析】选D.A的逆命题是若|a|=|b|,则a=b.假命题;B的逆命题是周长相等的三角形是全等三角形.假命题;C的逆命题是若ab=0,则a=0.假命题;D的逆命题是等腰三角形的其中两边相等.真命题.
二、6、互逆命题,逆命题.
7、120cm2
8、5或。解析:当第三条线段为直角边时,4为斜边,根据勾股定理得第三边长为=;当第三条线段为斜边时,根据勾股定理得第三边长为=5.
9、直角,∠A
10、【解析】∵(a-5)2+(b-12)2+|c-13|=0,
∴a=5,b=12,c=13,
∵52+122=132,∴△ABC是直角三角形.
答案:直角
三、11、解:(1)的逆命题是如果ab=0,那么a=0.不成立.(2)的逆命题是如果x2=16,那么x=4.不成立.(3)的逆命题是全等三角形的面积相等.成立.(4)的逆命题是如果三角形有两个内角是锐角,那么另一个内角是钝角.不成立.(5)的逆命题是在一个三角形中,等边对等角.成立.
点拨:要确定一个命题的逆命题,只要将原命题的题设与结论互换即可.
12、【答案】连接BD,
∵∠C=90°,
∴△BCD为直角三角形,
∵BD2=BC2+CD2=22+12=()2,
∵BD>0,
∴BD=,
在△ABD中,
∵AB2+BD2=20+5=25,AD2=52=25,
∴AB2+BD2=AD2,
∴△ABD为直角三角形,且∠ABD=90°,
∴S四边形ABCD=S△ABD+S△BCD=×2×+×2×1=6.
故四边形ABCD的面积是6。
13、解:如图所示,连接AC.
∵∠B=90°,
∴ΔABC是直角三角形.
依据勾股定理的AC2=AB2+BC2=42+32=25=52,∴AC=5.
在ΔACD中,AD2=132=169,CD2+AC2=122+52=169,∴AD2=AC2+CD2.
∴ΔACD是直角三角形,∠ACD=90°.
∴S四边形ABCD=SΔABC+SΔACD=AB?BC+AC?CD=×4×3+×5×12=6+30=36.
∴四边形ABCD的面积为36.
方法:要求不规则四边形ABCD的面积,可把四边形分割成几个三角形,这是常用的方法.此题是先利用勾股定理求出AC的长,再利用勾股定理的逆定理判断ΔACD为直角三角形,即原四边形ABCD可分割成两个直角三角形.[来源:学_科_网
14、7米,420元.
15、南偏东30°
16、【答案】(1)∵AD=4,AB=3,BD=5,DC=13,BC=12,
∴AB2+AD2=BD2,
BD2+BC2=DC2,
∴△ABD、△BDC是直角三角形,
∴∠A=90°,∠DBC=90°,
故这个零件符合要求。
(2)这个零件的面积=△ABD的面积+△BDC的面积
=3×4÷2+5×12÷2
=6+30
=36.
故这个零件的面积是36。
17、解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
18、解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三
角形面积公式有 BC·AB= AC·BD,
即6×8=10BD,解得BD=24/5
在Rt△BCD中,解CD=6.4(海里)
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
17.2 勾股定理的逆定理
一、选择题
1、下列定理中,有逆定理的个数是( )
①有两边相等的三角形是等腰三角形;②若三角形的三边长a,b,c满足a2+b2=c2,则该三角形是直角三角形;③全等三角形的对应角相等;④若a=b, a2 =b2.
A. 1个 B. 2个 C. 3个 D. 4个
2、在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A-∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2-c2,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形
D.如果a2:b2:c2=9:16:25,那么△ABC是直角三角形
3、下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6
C.5,12,13 D.4,6,7
4、一个三角形的三边的长分别是3,4,5,则这个三角形最长边上的高是 ( )
A.4 B.3 C.2.5 D.2.4
5、下列命题的逆命题是真命题的是 ( )
A.若a=b,则|a|=|b|
B.全等三角形的周长相等
C.若a=0,则ab=0
D.有两边相等的三角形是等腰三角形
填空题
6、在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论是第二个命题的题设,那么这两个命题叫做____________;如果把其中一个命题叫做原命题,那么另一个命题叫做它的____________.
7、一个三角形三条边的比为5:12:13,且周长为60cm,则它的面积是
8、 已知两条线段长分别为3,4,那么能与它们组成直角三角形的第三条线段长是
9、已知△ ABC中,BC=41,AC=40,AB=9,则此三角形为 三角形, 是最大角.
10、已知△ABC的三边a,b,c满足(a-5)2+(b-12)2+|c-13|=0,则△ABC是__________三角形.
三、解答题
11、写出下列命题的逆命题,并判断这些逆命题是否成立.
(1) 如果a=0,那么 ab=0;
(2) 如果x=4,那么x2=16;
(3) 面积相等的三角形是全等三角形;
(4) 如果三角形有一个内角是钝角,那么其余两个角是锐角;
(5) 在一个三角形中,等角对等边.
12、如图所示,在四边形ABCD中,AB=2,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积。
13、如图所示,在四边形 ABCD 中,∠B= 90°,AB=4,BC=3,CD=12,AD=13,求四边形ABCD的面积.
14、如图,在高为3米,斜坡长为5米的楼梯表面铺地毯,则地毯的长度至少需要多少米?若楼梯宽2米,地毯每平方米30元,那么这块地毯需花多少元?
15、在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里的速度前进,乙船沿南偏东某个角度以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?
16、一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角。工人师傅量得这个零件各边长如图2所示。
(1)你认为这个零件符合要求吗?为什么?
(2)求这个零件的面积。
17、 如图,在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=CB,试判断AF与EF的位置关系,并说明理由.
18、如图,南北方向PQ以东为我国领海,以西为公海,晚上10时28分,我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近,便立即通知在PQ上B处巡逻的103号艇注意其动向,经检测,AC=10海里,BC=8海里,AB=6海里,若该船只的速度为12.8海里/时,则可疑船只最早何时进入我领海?
参考答案:
一、1、B 解析 ①的逆命题是“等腰三角形有两边相等”,是真命题;②的逆命题是“若直角三角形的两条直角边长分别为a,b,斜边长为c,则三边长a,b,c满足a2+b2=c2”,是真命题;③对应角相等的两个三角形不一定全等;④若a2=b2,则a与b不一定相等,所以③④的逆命题是假命题,没有逆等理.
2、B【答案】B
【解析】如果∠A-∠B=∠C,那么△ABC是直角三角形,A正确;如果a2=b2-c2,那么△ABC是直角三角形且∠B=90°,B错误;如果∠A:∠B:∠C=1:3:2,设∠A=x,则∠B=2x,∠C=3x,则x+3x+2x=180°,解得,x=30°,则3x=90°,那么△ABC是直角三角形,C正确;如果a2:b2:c2=9:16:25,则如果a2+b2=c2,那么△ABC是直角三角形,D正确;故选:B。
C
D
【解析】选D.A的逆命题是若|a|=|b|,则a=b.假命题;B的逆命题是周长相等的三角形是全等三角形.假命题;C的逆命题是若ab=0,则a=0.假命题;D的逆命题是等腰三角形的其中两边相等.真命题.
二、6、互逆命题,逆命题.
7、120cm2
8、5或。解析:当第三条线段为直角边时,4为斜边,根据勾股定理得第三边长为=;当第三条线段为斜边时,根据勾股定理得第三边长为=5.
9、直角,∠A
10、【解析】∵(a-5)2+(b-12)2+|c-13|=0,
∴a=5,b=12,c=13,
∵52+122=132,∴△ABC是直角三角形.
答案:直角
三、11、解:(1)的逆命题是如果ab=0,那么a=0.不成立.(2)的逆命题是如果x2=16,那么x=4.不成立.(3)的逆命题是全等三角形的面积相等.成立.(4)的逆命题是如果三角形有两个内角是锐角,那么另一个内角是钝角.不成立.(5)的逆命题是在一个三角形中,等边对等角.成立.
点拨:要确定一个命题的逆命题,只要将原命题的题设与结论互换即可.
12、【答案】连接BD,
∵∠C=90°,
∴△BCD为直角三角形,
∵BD2=BC2+CD2=22+12=()2,
∵BD>0,
∴BD=,
在△ABD中,
∵AB2+BD2=20+5=25,AD2=52=25,
∴AB2+BD2=AD2,
∴△ABD为直角三角形,且∠ABD=90°,
∴S四边形ABCD=S△ABD+S△BCD=×2×+×2×1=6.
故四边形ABCD的面积是6。
13、解:如图所示,连接AC.
∵∠B=90°,
∴ΔABC是直角三角形.
依据勾股定理的AC2=AB2+BC2=42+32=25=52,∴AC=5.
在ΔACD中,AD2=132=169,CD2+AC2=122+52=169,∴AD2=AC2+CD2.
∴ΔACD是直角三角形,∠ACD=90°.
∴S四边形ABCD=SΔABC+SΔACD=AB?BC+AC?CD=×4×3+×5×12=6+30=36.
∴四边形ABCD的面积为36.
方法:要求不规则四边形ABCD的面积,可把四边形分割成几个三角形,这是常用的方法.此题是先利用勾股定理求出AC的长,再利用勾股定理的逆定理判断ΔACD为直角三角形,即原四边形ABCD可分割成两个直角三角形.[来源:学_科_网
14、7米,420元.
15、南偏东30°
16、【答案】(1)∵AD=4,AB=3,BD=5,DC=13,BC=12,
∴AB2+AD2=BD2,
BD2+BC2=DC2,
∴△ABD、△BDC是直角三角形,
∴∠A=90°,∠DBC=90°,
故这个零件符合要求。
(2)这个零件的面积=△ABD的面积+△BDC的面积
=3×4÷2+5×12÷2
=6+30
=36.
故这个零件的面积是36。
17、解:AF⊥EF.理由如下:
设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
18、解:∵AC=10,AB=6,BC=8,
∴AC2=AB2+BC2,
即△ABC是直角三角形.
设PQ与AC相交于点D,根据三
角形面积公式有 BC·AB= AC·BD,
即6×8=10BD,解得BD=24/5
在Rt△BCD中,解CD=6.4(海里)
又∵该船只的速度为12.8海里/时,
6.4÷12.8=0.5(小时)=30(分钟),
∴需要30分钟进入我领海,即最早晚上10时58分进入我领海.
