2020年春人教版八年级物理下册课件 10.2 阿基米德原理 共29页ppt
文档属性
| 名称 | 2020年春人教版八年级物理下册课件 10.2 阿基米德原理 共29页ppt |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-04 13:22:35 | ||
图片预览






文档简介
课件29张PPT。第十章 浮力10.2
阿基米德原理皇冠到底是真的还是假的
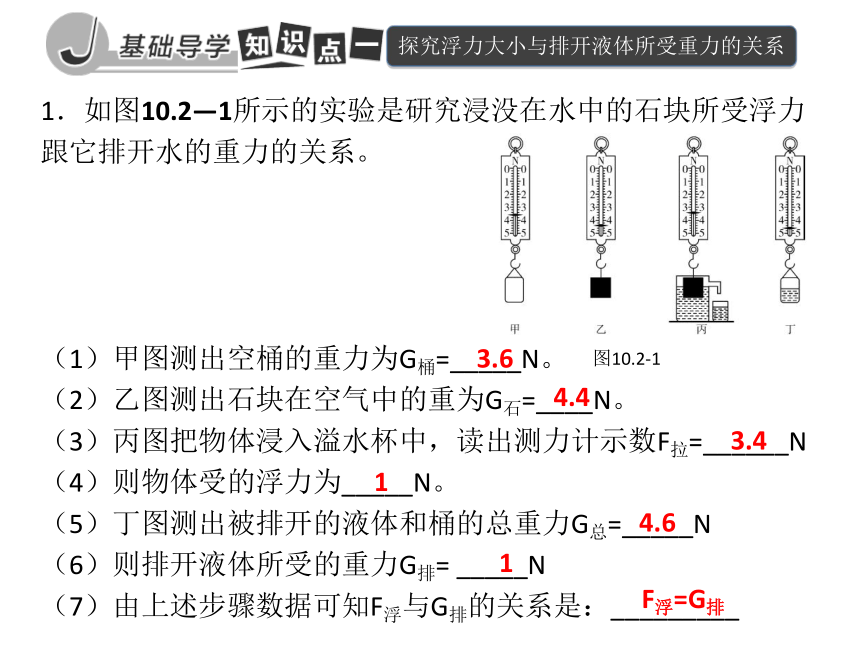
如何才能在不破坏皇冠的基础上测出它的体积呢?1.如图10.2—1所示的实验是研究浸没在水中的石块所受浮力跟它排开水的重力的关系。
(1)甲图测出空桶的重力为G桶=_____N。
(2)乙图测出石块在空气中的重为G石=____N。
(3)丙图把物体浸入溢水杯中,读出测力计示数F拉=______N
(4)则物体受的浮力为_____N。
(5)丁图测出被排开的液体和桶的总重力G总=_____N
(6)则排开液体所受的重力G排= _____N
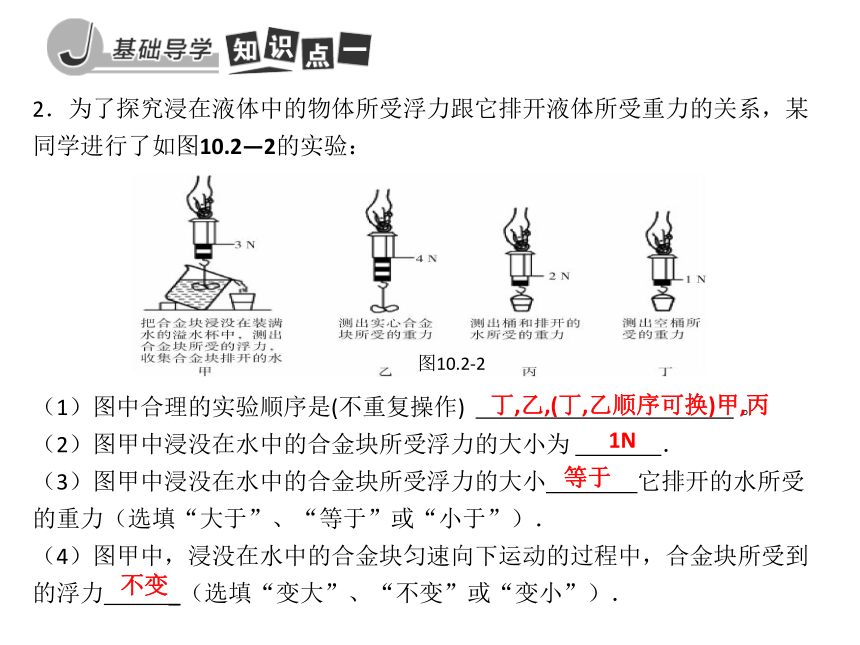
(7)由上述步骤数据可知F浮与G排的关系是:_________3.64.43.414.61F浮=G排图10.2-1探究浮力大小与排开液体所受重力的关系2.为了探究浸在液体中的物体所受浮力跟它排开液体所受重力的关系,某同学进行了如图10.2—2的实验:
(1)图中合理的实验顺序是(不重复操作) 。
(2)图甲中浸没在水中的合金块所受浮力的大小为 .
(3)图甲中浸没在水中的合金块所受浮力的大小 它排开的水所受的重力(选填“大于”、“等于”或“小于”).
(4)图甲中,浸没在水中的合金块匀速向下运动的过程中,合金块所受到的浮力 _(选填“变大”、“不变”或“变小”).图10.2-2丁,乙,(丁,乙顺序可换)甲,丙1N等于不变3.阿基米德原理:浸在液体里的物体受到竖直向 的浮力,浮力的大小等于它排开的 。用公式表示为F浮= 。上液体所受的重力G排=m排g=ρ浮gV排写出下列用不同方法计算浮力的公式:
1.弹簧测力计称重法测浮力: 。
2.压力差法计算浮力: 。
3.阿基米德原理: 。
4.当物体漂浮或悬浮在液体中: 。F浮=G物-F示F浮=F下表面-F上表面F浮=G排=m排g=ρ液gV排F浮=G物=m物g阿基米德原理——
浸在液体中的物体所受浮力大小 物体
公式: .
注意:1、无论物体浸入液体中,是部分浸入还是全部浸没,是下沉还是漂浮 。
2、物体浸入气体,受到气体的浮力大小也等于排开的气体所受的重力,即 , 。学习总结等于 排开的液体所
受到的重力 。F浮=G排=m排g=ρ液gV排任何状态,任何情况,阿基米德原理均适用对于气体阿基米德原理同样适用1.如图10.2-3所示,体积相同、形状不同的铅块、铁块和铝块,浸没在水中不同深度的地方,则 ( )
A.铝块受到的浮力最大,因为它浸入水中的深度最大
B.铅块受到的浮力最大,因为它的密度最大
C.铅块、铁块、铝块受的浮力一样大
D.因素太多,无法判断图10.2-3C2.有三个体积相同的木球、铜球和铁球,放入水中,静止时如图10.2-4所示,它们受到的浮力( )
A.木球受到的浮力最大
B.铁球受到的浮力最大
C.铜球和铁球受到的浮力一样大
D.三个球受到的浮力一样大图10.2-3C3.2010年5月,美国“海神”号潜艇在太平洋成功下潜至11 000 m深处,探秘世界上最深的马里亚纳海沟。从100 m深处下潜到11 000 m深处的过程,潜艇体积不变,则其受到的压强和浮力的变化情况是( )
A.压强逐渐变大,浮力逐渐变大
B.压强逐渐变大,浮力大小不变
C.压强逐渐变小,浮力逐渐变小
D.压强逐渐变小,浮力大小不变B3.2010年5月,美国“海神”号潜艇在太平洋成功下潜至11 000 m深处,探秘世界上最深的马里亚纳海沟。从100 m深处下潜到11 000 m深处的过程,潜艇体积不变,则其受到的压强和浮力的变化情况是( )
A.压强逐渐变大,浮力逐渐变大
B.压强逐渐变大,浮力大小不变
C.压强逐渐变小,浮力逐渐变小
D.压强逐渐变小,浮力大小不变B4.将一个质量为3 kg的物体放入一个装满酒精的溢酒精杯中后,从杯中溢出了1 kg的酒精,则物体在酒精中受到的浮力的大小为 N;
你的依据是 。(g=10 N/kg)10F浮=G排=m排g5.先在溢水杯中装满水(水面与溢水口齐平),水深为10 cm,再放入一木块,溢出的水全部用小烧杯接住(如图10.2-5所示)。测出小烧杯收集到的水的质量为300 g,则木块受到的浮力 N,木块的重力为 N。(g取10 N/kg)33图10.2-56.如图10.2-6所示,将三个体积相同的铁球分别浸没在盐水、纯水和煤油(密度是0.8×103 kg/m3)中,根据阿基米德原理公式 可知物体受到的浮力大小是由 和
这两个因素决定的,而它们的 相同, 最大,则铁球在 中受到的浮力最大。F浮=ρ液gV排图10.2-6ρ液V排V排盐水密度盐水7.悬浮在海水中的潜艇排开海水的重量为3×107 N(g取10 N/kg,海水的密度取1×103 kg/m3)。
(1)潜艇受到的浮力是多少?
(2)潜艇排开海水的质量和体积分别是多少?(1)悬浮时F浮=G物,又F浮=G排,
所以F浮=G排=G物=3×107 N。(2)m排=G排/g=3×107 N/10=3×106 kg;
V排=m排/ρ海水=3×106 kg/1000kg/m3=3000 m38.把一木块放入盛有水的量筒中,木块漂浮在水面上,量筒中的水面从40 mL处上升到90 mL处,则木块受到的浮力为多少?这个木块重为多少?(g取10 N/ kg,ρ水=1.0×103 kg/m3)解:V排=90 mL-40 mL=50 mL=5×10-5 m3,
F浮=ρ液gV排
=1.0×103 kg/m3×10 N/kg×5×10-5 m3
=0.5 N,
又因为木块处于漂浮状态,所以F浮=G木=0.5 N9.一块体积为0.03 m3的铁块,当它完全浸没在酒精中时,铁块受到的浮力是多少?(g=10 N/kg,ρ酒精=0.8×103 kg/m3)解:物体浸没时V物=V排=0.03 m3,
所以:F浮=ρ液gV排
=0.8×103 kg/m3×10 N/kg×0.03 m3
=240 N10.有一金属,在空气中称时,弹簧测力计的示数为4.9 N,浸没在水中称时,弹簧测力计的示数为3.92 N,求:(本题g=9.8 N/kg)
(1)金属块受到的浮力。
(2)金属块的体积是多少 cm3?
(3)金属块的密度是多少g/cm3?解:(1)F浮=G金-F拉=4.9 N-3.92 N=0.98 N。
(2)物体浸没时:
V物=V排=0.98N/ 1000kg/m3×9.8N/kg
=10-4m3=100 cm3
(3)p=m/V=G/gV=4.9N / 9.8N/kg×10-4m3
=5g/cm3解:(1)∵金属块处于静止状态, 受到的力相互平衡,
有F浮+F拉= G∴ F拉=F浮- G=5N-3N=2N
(2) ∵F浮=ρ液g V排
∴ V排=F浮/ρ液g =2N/( 1×103kg/m3× 10N/kg )=2 × 10-4m3
∵金属块浸没, ∴ V物=V排=2 × 10-4m3
金属块质量m=G/g=5N/10N/kg=0.5kg
密度ρ=m/V=0.5kg/2 × 10-4m31.(2017?潮州)如图10.2-7所示,用手提住弹簧测力计(图中手未画出),下面吊着一个金属块。当金属块未接触容器中的水时(如图甲),弹簧测力计的示数为5N;当金属块全部浸入水中时(如图丙),弹簧测力计的示数为3N。(已知ρ水=1.0×103kg/m3,g取10N/kg)
(1)求金属块全部浸入水中时受到的浮力;
(2)求金属块的体积和密度;
图10.2-7(3)在使金属块由图(乙)位置渐渐浸入水中至图(丙)位置的过程中,试分析水对容器底部压力的变化情况。 根据液体压强公式p=ρgh知:当从图乙起物体逐渐浸入水中, 水面升高, 容器底部离水面的深度h增大,水的密度ρ不变,所以容器底受到水的压强p变大。 当物体上表面浸入水中后,物体继续向下,水面不再升高,容器底部离水面的深度h不变,水的密度ρ不变,所以容器底受到水的压强p不变。图10.2-72.(2016?广州)除图10.2-8中的器材外,还可提供足够的水(密度为ρ水),测量漂浮在水面的玩具鸭所受重力。
(1)简要写出实验的合理方案(可用画图或文字表述);
(2)用题目所给及所测出的物理量推导出玩具鸭所受重力的表达式(玩具鸭不能放入量筒)。解:(1)实验方案:测出玩具鸭排开水的体积;
①标记下鸭漂浮在水面时的水位;
②把玩具鸭取出;
③用量筒量取水倒入水槽中( 可能要用量筒分多次取水), 让水位回复原标记位置,记录倒入的水体积V,V就是鸭排开的水的体积。
(2)因为玩具鸭处于静止状态,只受到浮力和重力,
根据二力平衡有:F浮=G鸭,
而F浮=ρ水g V排,所以G鸭=ρ水g V排图10.2-83.(2018·广州)如图10.2-9所示,小明每天测量同一个鸡蛋的质量,再把鸡蛋放入水中,观察它的浮沉情况后,取出放好。下表是他记录的部分数据及现象。(鸡蛋的体积保持不变,g=10 N/kg,ρ水=1.0×103 kg/m3)(1)求第57天鸡蛋所受浮力及鸡蛋的体积。(1)根据表格可知,第57天鸡蛋处于悬浮状态,
浮力大小为:F浮=G蛋=mg=0.062 kg×10 N/kg=0.62 N,
所以鸡蛋体积为解:(1)G=mg=62.0×10-3 kg×10 N/kg=0.62 N
因为鸡蛋悬浮,所以F浮=G=0.62 N
由F浮=G排=ρ液gV排得:
V=V排=F浮/ρ水g=6.2×10-5 m3。(2)比较第1天和第70天鸡蛋受到浮力的大小,写出判断依据。(2)第70天鸡蛋受到的浮力小于第1天受到的浮力.
根据公式F浮=G排=ρ水gV排,第70天鸡蛋排水的体积比第1天少,
而ρ水g不变,可知,第70天鸡蛋受到的浮力小于第1天受到的浮力。(3)根据表格的现象你如何判断鸡蛋存放时间的长短?(3)由表格中的数据和鸡蛋的状态可知,当鸡蛋在水中下沉时,鸡蛋放置不超过29天;鸡蛋悬浮时,鸡蛋的放置时间为58天以上阿基米德的故事
两千多年前的一天,在古希腊的叙拉古城上演了科学史上极其悲壮的一幕:一个罗马士兵闯入了一位老人的屋子,老人正在炭灰地上专心致志地画着几何图形。士兵的脚踩在了图上,老人气冲冲地喊道:“别弄乱了我的这些图!”勃然大怒的士兵,拔出剑刺向了手无寸铁的老人。就这样,这位七十五岁高龄的老人走完了自己的一生,临终前仍像他活着时一样,执着于他所喜爱的科学研究。
在这悲壮一幕中由于全神贯注于数学图形的冥想而殉难的老人就是同学们并不陌生的伟大科学家阿基米德。有关他的生平没有详细记载,但关于他的许多故事却广为流传。
最著名的自然是关于叙拉古城国王希伦的王冠的故事。国王怀疑金匠用一些合金偷换了他王冠上的黄金,就请阿基米德来测定王冠的真正含金量。阿基米德一直解不开这道难题。但有一天,在洗澡中他忽然找到了答案。兴奋之余,他从浴盆里跳出来,跑到了叙拉古城的大街上,边跑边欢呼:“尤里卡!尤里卡!”(这一古希腊语的意思是“我找到了!我找到了!”)不过遗憾的是,完全沉浸在新发现之中的阿基米德,竟然忘记了自己没穿衣服!他的这一发现在物理学课本上被称作“阿基米德原理”,是流体静力学中的第一个基本原理。
正如这则著名故事中我们所看到的,阿基米德能够在一段时间里非常专注地研究问题,以至于当他进行研究时,常常会忽略日常的生活问题。有人曾如此描绘过这位心不在焉的科学家的形象:“……忘记了吃饭,甚至忘记了他自己的存在,有时,人们会强制他洗浴或敷油,他都浑然不知,他会在火烧过的灰烬中,甚至在身上涂的油膏中寻找几何图形,完全进入了一种忘我的境界,更确切些说,他已如醉如痴地沉浸在对科学的热爱之中”。
正是凭着自己过人的天赋与这种勤奋、执着忘我的精神,阿基米德创作出了众多的科学杰作。作为物理学家,除了阿基米德原理外,他还发展了光学,创立了机械学,发明了水泵,发现了杠杆、滑轮的工作原理。为后一发现而感动的他曾发出豪言壮语:“给我一个立足点和一根足够长的杠杆,我就可以移动整个地球!”有些怀疑的国王想考验一下阿基米德的论断是否确实,于是挑选出一艘通常要用很多人花很大力气才能拖得动的船交给阿基米德做实际演习。阿基米德安装了一组滑轮,自己站在远处,手握绳子的一端,轻而易举地将船拖动了。据说国王佩服得五体投地,当即宣布:“从现在起,阿基米德说的话我们都要相信。”
在他为之献身的第二次布匿战争中,他那擅长将抽象的理论和工程技术的具体应用紧密结合在一起的天才又一次得到了充分的体现。他发明了许多杀伤力很强的武器为祖国效劳。传说他用起重机抓起敌人的船只摔得粉碎,发明奇妙的机器射出大石、火球,用巨大的火镜反射日光去焚毁敌船,等。最后,罗马敌兵成了惊弓之鸟。甚至看到一根绳子或一块木头从城里扔出来,立刻抱头鼠窜,并惊呼:“阿基米德的机器又瞄准我们了。” 除了可以脚踏实地地研究实际问题外,阿基米德还能够在最抽象、最微妙的数学领域中探索。他是有史以来最伟大的数学家之一。在其辉煌的数学生涯中,他将熟练的计算技巧和严格证明融为一体,将数学疆界向前推进了一大步。其几何著作是希腊数学的顶峰,体现了其非凡的创造力。他的数学著作很多,《论球与圆柱》是他最得意之作,在这本杰作中他推导出著名定理:“球的体积等于和它外切而等高的圆柱体体积的,球的表面积等于这个圆柱体的表面积的。”这标志着他数学事业的顶峰。阿基米德本人对这一发现也深感自豪,他希望后人能在他的墓碑上刻一个内接于圆柱的球体。当他悲剧性地结束了自己的生命后,据说当时的罗马统帅不但杀死了无知的士兵,而且遵从他的遗愿,为他建造了墓碑,上面刻着“圆柱和它的内切球”这样一个几何图形,以使后世永远缅怀他的伟大业绩! 阅读短文,回答下列问题: 阿基米德测定王冠含金量的方法有什么不足的地方? 1.无论物体浸入液体中,是部分浸入还是全部浸没,是下沉还是漂浮……任何状态,任何情况,阿基米德原理均适用。
2.物体浸入气体,受到气体的浮力大小也等于排开的气体所受的重力,即对于气体,阿基米德原理同样适用。
3.判断浮力大小的变化情况时,应根据实际情况选用公式。特别是利用阿基米德原理公式时,注意浮力的大小只与物体排开体积的大小和液体的密度有关,与其他因素无关。
阿基米德原理皇冠到底是真的还是假的
如何才能在不破坏皇冠的基础上测出它的体积呢?1.如图10.2—1所示的实验是研究浸没在水中的石块所受浮力跟它排开水的重力的关系。
(1)甲图测出空桶的重力为G桶=_____N。
(2)乙图测出石块在空气中的重为G石=____N。
(3)丙图把物体浸入溢水杯中,读出测力计示数F拉=______N
(4)则物体受的浮力为_____N。
(5)丁图测出被排开的液体和桶的总重力G总=_____N
(6)则排开液体所受的重力G排= _____N
(7)由上述步骤数据可知F浮与G排的关系是:_________3.64.43.414.61F浮=G排图10.2-1探究浮力大小与排开液体所受重力的关系2.为了探究浸在液体中的物体所受浮力跟它排开液体所受重力的关系,某同学进行了如图10.2—2的实验:
(1)图中合理的实验顺序是(不重复操作) 。
(2)图甲中浸没在水中的合金块所受浮力的大小为 .
(3)图甲中浸没在水中的合金块所受浮力的大小 它排开的水所受的重力(选填“大于”、“等于”或“小于”).
(4)图甲中,浸没在水中的合金块匀速向下运动的过程中,合金块所受到的浮力 _(选填“变大”、“不变”或“变小”).图10.2-2丁,乙,(丁,乙顺序可换)甲,丙1N等于不变3.阿基米德原理:浸在液体里的物体受到竖直向 的浮力,浮力的大小等于它排开的 。用公式表示为F浮= 。上液体所受的重力G排=m排g=ρ浮gV排写出下列用不同方法计算浮力的公式:
1.弹簧测力计称重法测浮力: 。
2.压力差法计算浮力: 。
3.阿基米德原理: 。
4.当物体漂浮或悬浮在液体中: 。F浮=G物-F示F浮=F下表面-F上表面F浮=G排=m排g=ρ液gV排F浮=G物=m物g阿基米德原理——
浸在液体中的物体所受浮力大小 物体
公式: .
注意:1、无论物体浸入液体中,是部分浸入还是全部浸没,是下沉还是漂浮 。
2、物体浸入气体,受到气体的浮力大小也等于排开的气体所受的重力,即 , 。学习总结等于 排开的液体所
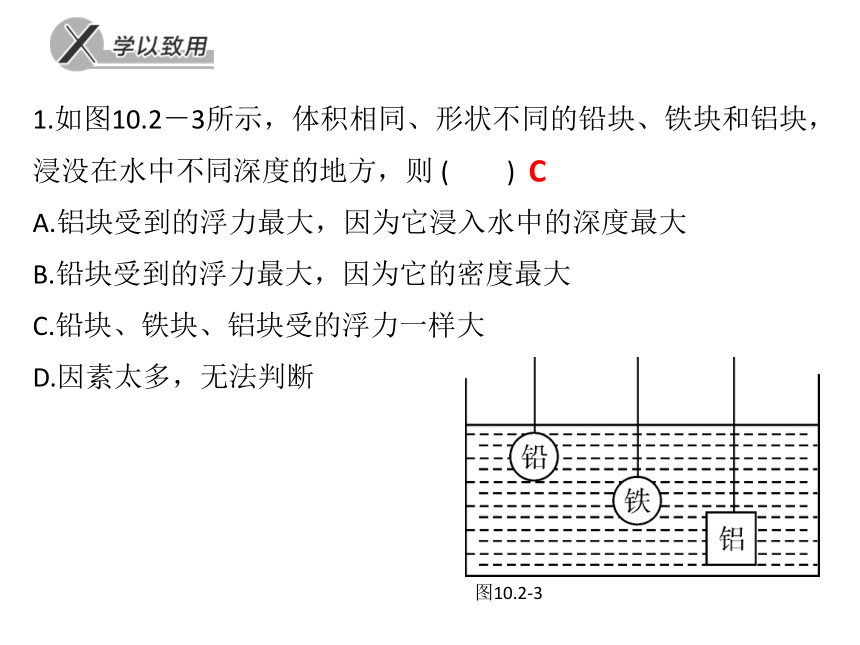
受到的重力 。F浮=G排=m排g=ρ液gV排任何状态,任何情况,阿基米德原理均适用对于气体阿基米德原理同样适用1.如图10.2-3所示,体积相同、形状不同的铅块、铁块和铝块,浸没在水中不同深度的地方,则 ( )
A.铝块受到的浮力最大,因为它浸入水中的深度最大
B.铅块受到的浮力最大,因为它的密度最大
C.铅块、铁块、铝块受的浮力一样大
D.因素太多,无法判断图10.2-3C2.有三个体积相同的木球、铜球和铁球,放入水中,静止时如图10.2-4所示,它们受到的浮力( )
A.木球受到的浮力最大
B.铁球受到的浮力最大
C.铜球和铁球受到的浮力一样大
D.三个球受到的浮力一样大图10.2-3C3.2010年5月,美国“海神”号潜艇在太平洋成功下潜至11 000 m深处,探秘世界上最深的马里亚纳海沟。从100 m深处下潜到11 000 m深处的过程,潜艇体积不变,则其受到的压强和浮力的变化情况是( )
A.压强逐渐变大,浮力逐渐变大
B.压强逐渐变大,浮力大小不变
C.压强逐渐变小,浮力逐渐变小
D.压强逐渐变小,浮力大小不变B3.2010年5月,美国“海神”号潜艇在太平洋成功下潜至11 000 m深处,探秘世界上最深的马里亚纳海沟。从100 m深处下潜到11 000 m深处的过程,潜艇体积不变,则其受到的压强和浮力的变化情况是( )
A.压强逐渐变大,浮力逐渐变大
B.压强逐渐变大,浮力大小不变
C.压强逐渐变小,浮力逐渐变小
D.压强逐渐变小,浮力大小不变B4.将一个质量为3 kg的物体放入一个装满酒精的溢酒精杯中后,从杯中溢出了1 kg的酒精,则物体在酒精中受到的浮力的大小为 N;
你的依据是 。(g=10 N/kg)10F浮=G排=m排g5.先在溢水杯中装满水(水面与溢水口齐平),水深为10 cm,再放入一木块,溢出的水全部用小烧杯接住(如图10.2-5所示)。测出小烧杯收集到的水的质量为300 g,则木块受到的浮力 N,木块的重力为 N。(g取10 N/kg)33图10.2-56.如图10.2-6所示,将三个体积相同的铁球分别浸没在盐水、纯水和煤油(密度是0.8×103 kg/m3)中,根据阿基米德原理公式 可知物体受到的浮力大小是由 和
这两个因素决定的,而它们的 相同, 最大,则铁球在 中受到的浮力最大。F浮=ρ液gV排图10.2-6ρ液V排V排盐水密度盐水7.悬浮在海水中的潜艇排开海水的重量为3×107 N(g取10 N/kg,海水的密度取1×103 kg/m3)。
(1)潜艇受到的浮力是多少?
(2)潜艇排开海水的质量和体积分别是多少?(1)悬浮时F浮=G物,又F浮=G排,
所以F浮=G排=G物=3×107 N。(2)m排=G排/g=3×107 N/10=3×106 kg;
V排=m排/ρ海水=3×106 kg/1000kg/m3=3000 m38.把一木块放入盛有水的量筒中,木块漂浮在水面上,量筒中的水面从40 mL处上升到90 mL处,则木块受到的浮力为多少?这个木块重为多少?(g取10 N/ kg,ρ水=1.0×103 kg/m3)解:V排=90 mL-40 mL=50 mL=5×10-5 m3,
F浮=ρ液gV排
=1.0×103 kg/m3×10 N/kg×5×10-5 m3
=0.5 N,
又因为木块处于漂浮状态,所以F浮=G木=0.5 N9.一块体积为0.03 m3的铁块,当它完全浸没在酒精中时,铁块受到的浮力是多少?(g=10 N/kg,ρ酒精=0.8×103 kg/m3)解:物体浸没时V物=V排=0.03 m3,
所以:F浮=ρ液gV排
=0.8×103 kg/m3×10 N/kg×0.03 m3
=240 N10.有一金属,在空气中称时,弹簧测力计的示数为4.9 N,浸没在水中称时,弹簧测力计的示数为3.92 N,求:(本题g=9.8 N/kg)
(1)金属块受到的浮力。
(2)金属块的体积是多少 cm3?
(3)金属块的密度是多少g/cm3?解:(1)F浮=G金-F拉=4.9 N-3.92 N=0.98 N。
(2)物体浸没时:
V物=V排=0.98N/ 1000kg/m3×9.8N/kg
=10-4m3=100 cm3
(3)p=m/V=G/gV=4.9N / 9.8N/kg×10-4m3
=5g/cm3解:(1)∵金属块处于静止状态, 受到的力相互平衡,
有F浮+F拉= G∴ F拉=F浮- G=5N-3N=2N
(2) ∵F浮=ρ液g V排
∴ V排=F浮/ρ液g =2N/( 1×103kg/m3× 10N/kg )=2 × 10-4m3
∵金属块浸没, ∴ V物=V排=2 × 10-4m3
金属块质量m=G/g=5N/10N/kg=0.5kg
密度ρ=m/V=0.5kg/2 × 10-4m31.(2017?潮州)如图10.2-7所示,用手提住弹簧测力计(图中手未画出),下面吊着一个金属块。当金属块未接触容器中的水时(如图甲),弹簧测力计的示数为5N;当金属块全部浸入水中时(如图丙),弹簧测力计的示数为3N。(已知ρ水=1.0×103kg/m3,g取10N/kg)
(1)求金属块全部浸入水中时受到的浮力;
(2)求金属块的体积和密度;
图10.2-7(3)在使金属块由图(乙)位置渐渐浸入水中至图(丙)位置的过程中,试分析水对容器底部压力的变化情况。 根据液体压强公式p=ρgh知:当从图乙起物体逐渐浸入水中, 水面升高, 容器底部离水面的深度h增大,水的密度ρ不变,所以容器底受到水的压强p变大。 当物体上表面浸入水中后,物体继续向下,水面不再升高,容器底部离水面的深度h不变,水的密度ρ不变,所以容器底受到水的压强p不变。图10.2-72.(2016?广州)除图10.2-8中的器材外,还可提供足够的水(密度为ρ水),测量漂浮在水面的玩具鸭所受重力。
(1)简要写出实验的合理方案(可用画图或文字表述);
(2)用题目所给及所测出的物理量推导出玩具鸭所受重力的表达式(玩具鸭不能放入量筒)。解:(1)实验方案:测出玩具鸭排开水的体积;
①标记下鸭漂浮在水面时的水位;
②把玩具鸭取出;
③用量筒量取水倒入水槽中( 可能要用量筒分多次取水), 让水位回复原标记位置,记录倒入的水体积V,V就是鸭排开的水的体积。
(2)因为玩具鸭处于静止状态,只受到浮力和重力,
根据二力平衡有:F浮=G鸭,
而F浮=ρ水g V排,所以G鸭=ρ水g V排图10.2-83.(2018·广州)如图10.2-9所示,小明每天测量同一个鸡蛋的质量,再把鸡蛋放入水中,观察它的浮沉情况后,取出放好。下表是他记录的部分数据及现象。(鸡蛋的体积保持不变,g=10 N/kg,ρ水=1.0×103 kg/m3)(1)求第57天鸡蛋所受浮力及鸡蛋的体积。(1)根据表格可知,第57天鸡蛋处于悬浮状态,
浮力大小为:F浮=G蛋=mg=0.062 kg×10 N/kg=0.62 N,
所以鸡蛋体积为解:(1)G=mg=62.0×10-3 kg×10 N/kg=0.62 N
因为鸡蛋悬浮,所以F浮=G=0.62 N
由F浮=G排=ρ液gV排得:
V=V排=F浮/ρ水g=6.2×10-5 m3。(2)比较第1天和第70天鸡蛋受到浮力的大小,写出判断依据。(2)第70天鸡蛋受到的浮力小于第1天受到的浮力.
根据公式F浮=G排=ρ水gV排,第70天鸡蛋排水的体积比第1天少,
而ρ水g不变,可知,第70天鸡蛋受到的浮力小于第1天受到的浮力。(3)根据表格的现象你如何判断鸡蛋存放时间的长短?(3)由表格中的数据和鸡蛋的状态可知,当鸡蛋在水中下沉时,鸡蛋放置不超过29天;鸡蛋悬浮时,鸡蛋的放置时间为58天以上阿基米德的故事
两千多年前的一天,在古希腊的叙拉古城上演了科学史上极其悲壮的一幕:一个罗马士兵闯入了一位老人的屋子,老人正在炭灰地上专心致志地画着几何图形。士兵的脚踩在了图上,老人气冲冲地喊道:“别弄乱了我的这些图!”勃然大怒的士兵,拔出剑刺向了手无寸铁的老人。就这样,这位七十五岁高龄的老人走完了自己的一生,临终前仍像他活着时一样,执着于他所喜爱的科学研究。
在这悲壮一幕中由于全神贯注于数学图形的冥想而殉难的老人就是同学们并不陌生的伟大科学家阿基米德。有关他的生平没有详细记载,但关于他的许多故事却广为流传。
最著名的自然是关于叙拉古城国王希伦的王冠的故事。国王怀疑金匠用一些合金偷换了他王冠上的黄金,就请阿基米德来测定王冠的真正含金量。阿基米德一直解不开这道难题。但有一天,在洗澡中他忽然找到了答案。兴奋之余,他从浴盆里跳出来,跑到了叙拉古城的大街上,边跑边欢呼:“尤里卡!尤里卡!”(这一古希腊语的意思是“我找到了!我找到了!”)不过遗憾的是,完全沉浸在新发现之中的阿基米德,竟然忘记了自己没穿衣服!他的这一发现在物理学课本上被称作“阿基米德原理”,是流体静力学中的第一个基本原理。
正如这则著名故事中我们所看到的,阿基米德能够在一段时间里非常专注地研究问题,以至于当他进行研究时,常常会忽略日常的生活问题。有人曾如此描绘过这位心不在焉的科学家的形象:“……忘记了吃饭,甚至忘记了他自己的存在,有时,人们会强制他洗浴或敷油,他都浑然不知,他会在火烧过的灰烬中,甚至在身上涂的油膏中寻找几何图形,完全进入了一种忘我的境界,更确切些说,他已如醉如痴地沉浸在对科学的热爱之中”。
正是凭着自己过人的天赋与这种勤奋、执着忘我的精神,阿基米德创作出了众多的科学杰作。作为物理学家,除了阿基米德原理外,他还发展了光学,创立了机械学,发明了水泵,发现了杠杆、滑轮的工作原理。为后一发现而感动的他曾发出豪言壮语:“给我一个立足点和一根足够长的杠杆,我就可以移动整个地球!”有些怀疑的国王想考验一下阿基米德的论断是否确实,于是挑选出一艘通常要用很多人花很大力气才能拖得动的船交给阿基米德做实际演习。阿基米德安装了一组滑轮,自己站在远处,手握绳子的一端,轻而易举地将船拖动了。据说国王佩服得五体投地,当即宣布:“从现在起,阿基米德说的话我们都要相信。”
在他为之献身的第二次布匿战争中,他那擅长将抽象的理论和工程技术的具体应用紧密结合在一起的天才又一次得到了充分的体现。他发明了许多杀伤力很强的武器为祖国效劳。传说他用起重机抓起敌人的船只摔得粉碎,发明奇妙的机器射出大石、火球,用巨大的火镜反射日光去焚毁敌船,等。最后,罗马敌兵成了惊弓之鸟。甚至看到一根绳子或一块木头从城里扔出来,立刻抱头鼠窜,并惊呼:“阿基米德的机器又瞄准我们了。” 除了可以脚踏实地地研究实际问题外,阿基米德还能够在最抽象、最微妙的数学领域中探索。他是有史以来最伟大的数学家之一。在其辉煌的数学生涯中,他将熟练的计算技巧和严格证明融为一体,将数学疆界向前推进了一大步。其几何著作是希腊数学的顶峰,体现了其非凡的创造力。他的数学著作很多,《论球与圆柱》是他最得意之作,在这本杰作中他推导出著名定理:“球的体积等于和它外切而等高的圆柱体体积的,球的表面积等于这个圆柱体的表面积的。”这标志着他数学事业的顶峰。阿基米德本人对这一发现也深感自豪,他希望后人能在他的墓碑上刻一个内接于圆柱的球体。当他悲剧性地结束了自己的生命后,据说当时的罗马统帅不但杀死了无知的士兵,而且遵从他的遗愿,为他建造了墓碑,上面刻着“圆柱和它的内切球”这样一个几何图形,以使后世永远缅怀他的伟大业绩! 阅读短文,回答下列问题: 阿基米德测定王冠含金量的方法有什么不足的地方? 1.无论物体浸入液体中,是部分浸入还是全部浸没,是下沉还是漂浮……任何状态,任何情况,阿基米德原理均适用。
2.物体浸入气体,受到气体的浮力大小也等于排开的气体所受的重力,即对于气体,阿基米德原理同样适用。
3.判断浮力大小的变化情况时,应根据实际情况选用公式。特别是利用阿基米德原理公式时,注意浮力的大小只与物体排开体积的大小和液体的密度有关,与其他因素无关。
