湘教版八年级数学下册 4.1函数和它的表示方法课件(2课时、共38张ppt)
文档属性
| 名称 | 湘教版八年级数学下册 4.1函数和它的表示方法课件(2课时、共38张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-02 00:00:00 | ||
图片预览









文档简介
(共38张PPT)
4.1函数和它的表示法
第1课时
万物皆变
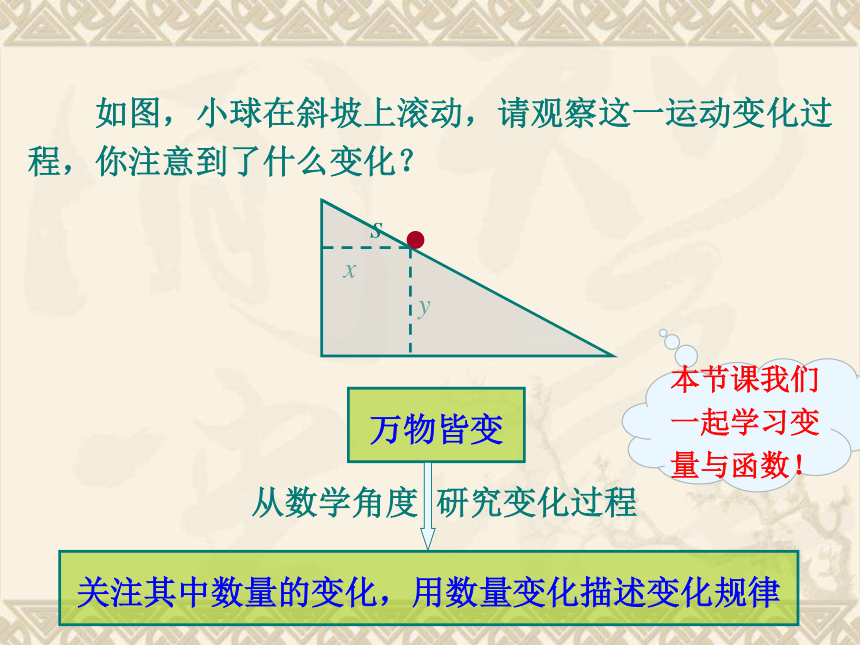
如图,小球在斜坡上滚动,请观察这一运动变化过
程,你注意到了什么变化?
万物皆变
关注其中数量的变化,用数量变化描述变化规律
从数学角度 研究变化过程
本节课我们一起学习变量与函数!
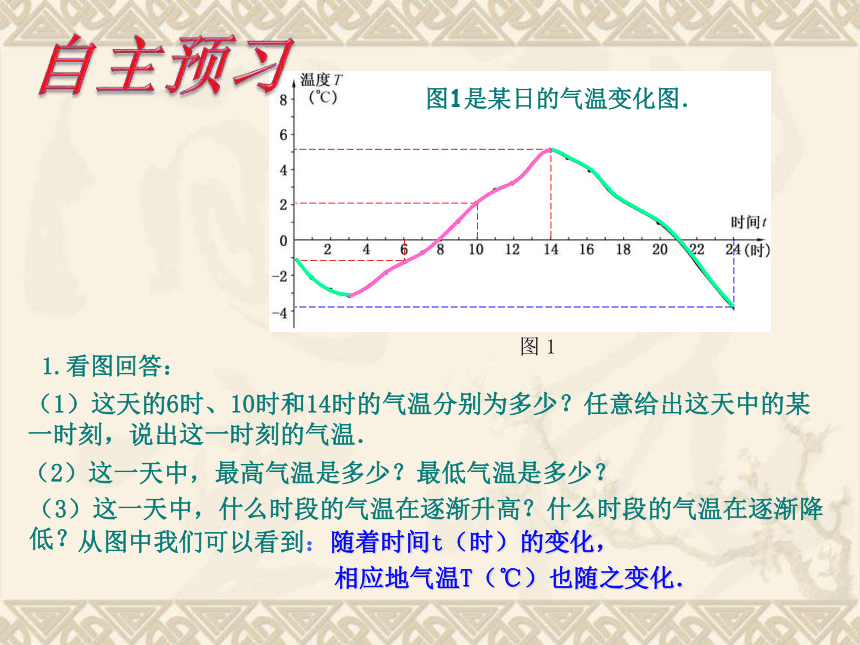
图1是某日的气温变化图.
1.看图回答:
(1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温.
(2)这一天中,最高气温是多少?最低气温是多少?
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
从图中我们可以看到:随着时间t(时)的变化,
相应地气温T(℃)也随之变化.
2.银行对各种不同的存款方式都规定了相应的利率,下表是2002年7月中国工商银行为“整存整取”的存款方式规定的利率:
观察上表,说说随着存期x的增长,相应的利率y是如何变化的.
随着存期x的增长,相应的利率y增大。
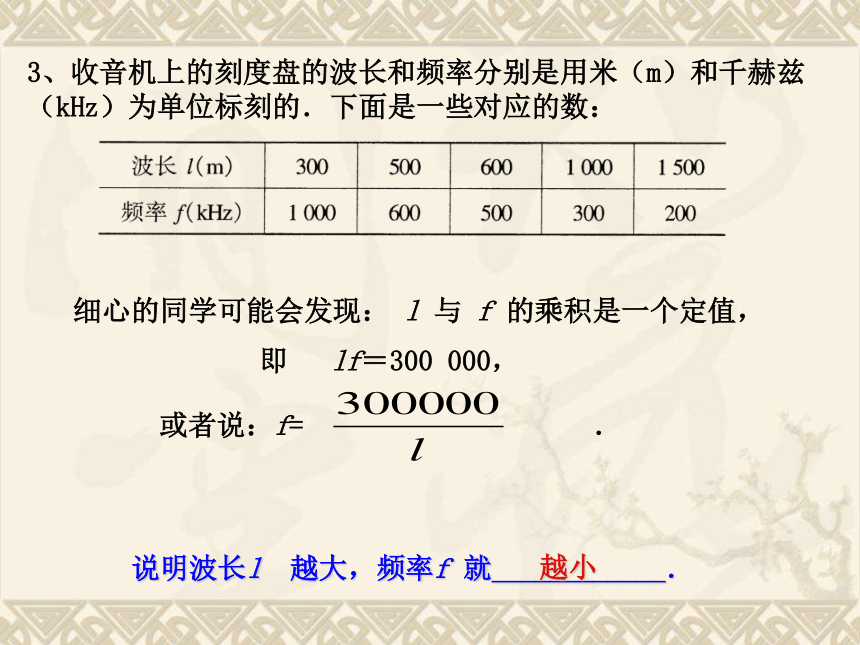
3、收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:
细心的同学可能会发现: l 与 f 的乘积是一个定值,
即 lf=300 000,
说明波长l 越大,频率f 就____________.
越小
我们研究了一些数量关系,它们都刻画了某些变化规律.
这里出现了各种各样的量,特别值得注意的是出现了一些数值会发生变化的量.
例如 问题1中,刻画气温变化规律的量是时间t和气温T,气温T随着时间t的变化而变化,它们都会取不同的数值.
像这样在某一变化过程中,取值会发生变化的量叫做变量(variable).
在其他三个问题中,有哪些变量?
上面问题中,都出现了两个变量,它们互相依赖,密切相关.
一般地,如果变量y随着变量x而变化,并且对于x的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数(function),记作y=f(x)。这时把x叫作自变量,把y叫做自变量。对于自变量x的每一个值a,因变量y的对应值称为函数值。和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量(independent variable),y是因变量(dependent variable),此时也称y是x的函数(function).
说一说
1、在问题1中,_________是自变量,_______是_______的函数。
2、在问题2中,存款是________,相应的利率是存款的______.
3、在问题3中,________是自变量,_________是_________的函数。
时间
温度
时间
自变量
函数
波长l
频率f
波长l
例1 已知圆柱的高是4cm,底面半径是r(cm),当圆柱的底面半径r由小变大时,圆柱的体积v(cm 3 )是r的函数。
(1)用含r的代数式来表示圆柱的体积v,指出自变量r的取值范围。
(2)当r=5,10时,V是多少?(结果保留∏)
1. 指出下列问题中的变量和常量:
(1)购买一些铅笔,单价为0.2元/支,记某同学购买铅笔的数量为x支,应付的总价为y元;
(2)用长为50 cm的铁丝围成一个等腰三角形,记这个等腰三角形的腰长为x cm,底边长为y cm;
(3)如图,△ABC中,∠ACB=90°,AC=3cm,BC=4cm.现有一动点P从点B出发,沿射线BA方向以1 cm/s的速度运动,到达点A随即停止运动.记点P的运动时间为x(s),△ACP的面积为y(cm?).
(4)出售某种文具盒,若每个获利 x元,一天可售出(6-x)个,一天出售该种文具盒的总利润为 y元.
2.如图,正形ABCD的边长为4 cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,当P、Q到达点C时都停止运动.设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2).
(1)在这个运动变化过程中,当运动时间x发生变化时,四边形PBDQ的面积y是否也随之发生变化?当运动时间x增大时,四边形PBDQ的面积y如何变化?
(2)在这个运动变化过程中,运动时间x的取值有什么要求吗?为什么?
问题2:在一个变化过程中,量与量之间是否是相互依存和变化的?是否存在变化规律?量的变化是否有限制条件?如何确定变量的变化条件?
课堂小结:
问题1:在一个变化过程中,什么是变量?什么是常量?常量是否都是显现的?请举例说明.
4.1函数和它的表示法 第2课时
问题1:上节课我们学习了函数的概念,你能说出什么叫做函数吗?
一般地, 如果变量y随着变量x而变化, 并且对于x取的每一个值, y都有唯一的一个值与它对应, 那么称y是x的函数.
问题2:(1)中,是怎样表示气温T与时间t之间的函数关系的?
用平面直角坐标系中的一个图形来表示.
问题2:(2)中,是怎样表示利率y与存期x之间的函数
关系的?
列一张表来表示.
( 2)银行对各种不同的存款方式都规定了相应的利率,下表是2002年7月中国工商银行为“整存整取”的存款方式规定的利率:
问题2:(3)中,是怎样表示频率f与波长x的函数关系的?
用一个式子 来表示.
(3)收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:
问题3:你能谈谈用图象法、列表法、公式法表示函数关系时各自的优点吗?
用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化;
用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值;
用公式法表示函数关系,可以方便地计算函数值.
函数的三种表示方法
列表法
图象法
公式法
函数的三种表示方法:图象法、列表法、公式法。
表示方法 定义 特点
________ 通过列表给出自变量
与函数的对应值。 能直接显示自变量的值
和与之对应的函数值。
________ 用图象表示两个变量
之间的关系。 形象直观地显示数据的
变化规律。
________ 用式子表示函数关系的方法。
简单明了,能准确地反映
整个变化过程中自变量
与函数的对应关系。
问题4:你能举出一些用图象法、列表法、表达式表示函数关系的例子吗?
举例:
(1)某班8名学生的身高y(单位:厘米)与学号x的函数关系如下表:如下表:
(2)一支铅笔2元,买x支铅笔所需的费用为y元,则y与x的函数关系可表示为:y=2x(x为正整数).
学号x 1 2 3 4 5 6 7 8
身高y 150 152 165 178 159 163 138 166
问题4:你能举出一些用图像法、列表法、表达式表示函数关系的例子吗?
举例:
(3)下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数y是日期x的函数.
问题5:是不是所有的函数都可以用函数表达式的形式表示出来呢?
举例:
S=x2
这个函数可以用函数表达式的形式表示.
问题5:是不是所有的函数都可以用函数表达式的形式表示出来呢?
举例:
这些函数不能用函数表达式的形式表示
学号x 1 2 3 4 5 6 7 8
身高y 150 152 165 178 159 163 138 166
请建立平面直角坐标系,任意画出一个函数图象
(1)请判断你周围的同学画的图象是不是函数图象?
(2)下面的图象中,y是x的函数吗?
(3)怎么判断一个图象是否是函数图象?
1.用边长为1 的等边三角形拼成如图所示的图形, 用y 表示拼成的图形的周长, 用n表示其中等边三角形的数目, 显然拼成的图形的周长y是n的函数.
3 4 5 6 7 8 9 10
y=n+2(n为正整数)
y=n+2(n为正整数)
例1 某天7时, 小明从家骑自行车上学, 途中因自行车发生故障, 修车耽误了一段时间后继续骑行, 按时赶到了学校. 图反映了他骑车的整个过程, 结合图象, 回答下列问题:
解(1)从横坐标看出, 自行车发生故障的时间是7:05; 从纵坐标看出, 此时离家1000 m.
(1) 自行车发生故障是在什么时间? 此时离家有多远?
例1 某天7时, 小明从家骑自行车上学, 途中因自行车发生故障, 修车耽误了一段时间后继续骑行, 按时赶到了学校. 图反映了他骑车的整个过程, 结合图象, 回答下列问题:
(2) 修车花了多长时间? 修好车后又花了多长时间到达学校?
解(2)从横坐标看出, 小明修车花了15 min; 小明修好车后又花了10 min到达学校.
例1 某天7时, 小明从家骑自行车上学, 途中因自行车发生故障, 修车耽误了一段时间后继续骑行, 按时赶到了学校. 图反映了他骑车的整个过程, 结合图象, 回答下列问题:
(3) 小明从家到学校的平均速度是多少?
解(3)从纵坐标看出, 小明家离学校2100 m; 从横坐标看出, 他在路上共花了30 min, 因此, 他从家到学校的平均速度是2 100 ÷ 30 = 70 (m/min).
例2 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y (米)与爬山所用时间x (分)的关系(从小强开始爬山时计时).
⑴ 小强让爷爷先上多少米?
⑵ 山顶离山脚的距离有多少米?谁先爬上山顶?
解:
⑴ 小强让爷爷先上60米;
⑵ 山顶离山脚的距离有300米,小强先爬上山顶;
(3)小强通过多少时间追上爷爷?
解:
(3)小强经过8分钟追上爷爷.
例2 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y (米)与爬山所用时间x (分)的关系(从小强开始爬山时计时).
1、
用固定的速度向如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( ).
C
2、
甲、乙两人在一次百米赛跑中,路程S(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是( )
A.甲、乙两人的速度相同
B.甲先到达终点
C.乙用的时间短
D.乙比甲跑的路程多
B
3、
小芳的爷爷每天坚持体育锻炼,某天他慢步行走到离家较远的公园,打了一会儿太极拳,然后沿原路跑步到家里,下面能够反映当天小芳爷爷离家的距离y(米)与时间x(分钟)之间的关系的大致图象是( )
C
A B C D
有下列说法:
①“龟兔再次赛跑”的路为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .
(把你认为正确说法的序号都填上)
4、
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了
“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的
时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).
①③④
(1)当用电量是180千瓦时时,电费
是 元;
(2)第二档的用电量范围是 ;
(3)“基本电价”是 元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
5、
为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如右折线图,请根据图像回答下列问题;
108
1800.6
500千瓦时
结 束
小结:
函数有哪些表示法?
4.1函数和它的表示法
第1课时
万物皆变
如图,小球在斜坡上滚动,请观察这一运动变化过
程,你注意到了什么变化?
万物皆变
关注其中数量的变化,用数量变化描述变化规律
从数学角度 研究变化过程
本节课我们一起学习变量与函数!
图1是某日的气温变化图.
1.看图回答:
(1)这天的6时、10时和14时的气温分别为多少?任意给出这天中的某一时刻,说出这一时刻的气温.
(2)这一天中,最高气温是多少?最低气温是多少?
(3)这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?
从图中我们可以看到:随着时间t(时)的变化,
相应地气温T(℃)也随之变化.
2.银行对各种不同的存款方式都规定了相应的利率,下表是2002年7月中国工商银行为“整存整取”的存款方式规定的利率:
观察上表,说说随着存期x的增长,相应的利率y是如何变化的.
随着存期x的增长,相应的利率y增大。
3、收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:
细心的同学可能会发现: l 与 f 的乘积是一个定值,
即 lf=300 000,
说明波长l 越大,频率f 就____________.
越小
我们研究了一些数量关系,它们都刻画了某些变化规律.
这里出现了各种各样的量,特别值得注意的是出现了一些数值会发生变化的量.
例如 问题1中,刻画气温变化规律的量是时间t和气温T,气温T随着时间t的变化而变化,它们都会取不同的数值.
像这样在某一变化过程中,取值会发生变化的量叫做变量(variable).
在其他三个问题中,有哪些变量?
上面问题中,都出现了两个变量,它们互相依赖,密切相关.
一般地,如果变量y随着变量x而变化,并且对于x的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数(function),记作y=f(x)。这时把x叫作自变量,把y叫做自变量。对于自变量x的每一个值a,因变量y的对应值称为函数值。和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量(independent variable),y是因变量(dependent variable),此时也称y是x的函数(function).
说一说
1、在问题1中,_________是自变量,_______是_______的函数。
2、在问题2中,存款是________,相应的利率是存款的______.
3、在问题3中,________是自变量,_________是_________的函数。
时间
温度
时间
自变量
函数
波长l
频率f
波长l
例1 已知圆柱的高是4cm,底面半径是r(cm),当圆柱的底面半径r由小变大时,圆柱的体积v(cm 3 )是r的函数。
(1)用含r的代数式来表示圆柱的体积v,指出自变量r的取值范围。
(2)当r=5,10时,V是多少?(结果保留∏)
1. 指出下列问题中的变量和常量:
(1)购买一些铅笔,单价为0.2元/支,记某同学购买铅笔的数量为x支,应付的总价为y元;
(2)用长为50 cm的铁丝围成一个等腰三角形,记这个等腰三角形的腰长为x cm,底边长为y cm;
(3)如图,△ABC中,∠ACB=90°,AC=3cm,BC=4cm.现有一动点P从点B出发,沿射线BA方向以1 cm/s的速度运动,到达点A随即停止运动.记点P的运动时间为x(s),△ACP的面积为y(cm?).
(4)出售某种文具盒,若每个获利 x元,一天可售出(6-x)个,一天出售该种文具盒的总利润为 y元.
2.如图,正形ABCD的边长为4 cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,当P、Q到达点C时都停止运动.设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2).
(1)在这个运动变化过程中,当运动时间x发生变化时,四边形PBDQ的面积y是否也随之发生变化?当运动时间x增大时,四边形PBDQ的面积y如何变化?
(2)在这个运动变化过程中,运动时间x的取值有什么要求吗?为什么?
问题2:在一个变化过程中,量与量之间是否是相互依存和变化的?是否存在变化规律?量的变化是否有限制条件?如何确定变量的变化条件?
课堂小结:
问题1:在一个变化过程中,什么是变量?什么是常量?常量是否都是显现的?请举例说明.
4.1函数和它的表示法 第2课时
问题1:上节课我们学习了函数的概念,你能说出什么叫做函数吗?
一般地, 如果变量y随着变量x而变化, 并且对于x取的每一个值, y都有唯一的一个值与它对应, 那么称y是x的函数.
问题2:(1)中,是怎样表示气温T与时间t之间的函数关系的?
用平面直角坐标系中的一个图形来表示.
问题2:(2)中,是怎样表示利率y与存期x之间的函数
关系的?
列一张表来表示.
( 2)银行对各种不同的存款方式都规定了相应的利率,下表是2002年7月中国工商银行为“整存整取”的存款方式规定的利率:
问题2:(3)中,是怎样表示频率f与波长x的函数关系的?
用一个式子 来表示.
(3)收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:
问题3:你能谈谈用图象法、列表法、公式法表示函数关系时各自的优点吗?
用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化;
用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值;
用公式法表示函数关系,可以方便地计算函数值.
函数的三种表示方法
列表法
图象法
公式法
函数的三种表示方法:图象法、列表法、公式法。
表示方法 定义 特点
________ 通过列表给出自变量
与函数的对应值。 能直接显示自变量的值
和与之对应的函数值。
________ 用图象表示两个变量
之间的关系。 形象直观地显示数据的
变化规律。
________ 用式子表示函数关系的方法。
简单明了,能准确地反映
整个变化过程中自变量
与函数的对应关系。
问题4:你能举出一些用图象法、列表法、表达式表示函数关系的例子吗?
举例:
(1)某班8名学生的身高y(单位:厘米)与学号x的函数关系如下表:如下表:
(2)一支铅笔2元,买x支铅笔所需的费用为y元,则y与x的函数关系可表示为:y=2x(x为正整数).
学号x 1 2 3 4 5 6 7 8
身高y 150 152 165 178 159 163 138 166
问题4:你能举出一些用图像法、列表法、表达式表示函数关系的例子吗?
举例:
(3)下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数y是日期x的函数.
问题5:是不是所有的函数都可以用函数表达式的形式表示出来呢?
举例:
S=x2
这个函数可以用函数表达式的形式表示.
问题5:是不是所有的函数都可以用函数表达式的形式表示出来呢?
举例:
这些函数不能用函数表达式的形式表示
学号x 1 2 3 4 5 6 7 8
身高y 150 152 165 178 159 163 138 166
请建立平面直角坐标系,任意画出一个函数图象
(1)请判断你周围的同学画的图象是不是函数图象?
(2)下面的图象中,y是x的函数吗?
(3)怎么判断一个图象是否是函数图象?
1.用边长为1 的等边三角形拼成如图所示的图形, 用y 表示拼成的图形的周长, 用n表示其中等边三角形的数目, 显然拼成的图形的周长y是n的函数.
3 4 5 6 7 8 9 10
y=n+2(n为正整数)
y=n+2(n为正整数)
例1 某天7时, 小明从家骑自行车上学, 途中因自行车发生故障, 修车耽误了一段时间后继续骑行, 按时赶到了学校. 图反映了他骑车的整个过程, 结合图象, 回答下列问题:
解(1)从横坐标看出, 自行车发生故障的时间是7:05; 从纵坐标看出, 此时离家1000 m.
(1) 自行车发生故障是在什么时间? 此时离家有多远?
例1 某天7时, 小明从家骑自行车上学, 途中因自行车发生故障, 修车耽误了一段时间后继续骑行, 按时赶到了学校. 图反映了他骑车的整个过程, 结合图象, 回答下列问题:
(2) 修车花了多长时间? 修好车后又花了多长时间到达学校?
解(2)从横坐标看出, 小明修车花了15 min; 小明修好车后又花了10 min到达学校.
例1 某天7时, 小明从家骑自行车上学, 途中因自行车发生故障, 修车耽误了一段时间后继续骑行, 按时赶到了学校. 图反映了他骑车的整个过程, 结合图象, 回答下列问题:
(3) 小明从家到学校的平均速度是多少?
解(3)从纵坐标看出, 小明家离学校2100 m; 从横坐标看出, 他在路上共花了30 min, 因此, 他从家到学校的平均速度是2 100 ÷ 30 = 70 (m/min).
例2 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y (米)与爬山所用时间x (分)的关系(从小强开始爬山时计时).
⑴ 小强让爷爷先上多少米?
⑵ 山顶离山脚的距离有多少米?谁先爬上山顶?
解:
⑴ 小强让爷爷先上60米;
⑵ 山顶离山脚的距离有300米,小强先爬上山顶;
(3)小强通过多少时间追上爷爷?
解:
(3)小强经过8分钟追上爷爷.
例2 王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y (米)与爬山所用时间x (分)的关系(从小强开始爬山时计时).
1、
用固定的速度向如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( ).
C
2、
甲、乙两人在一次百米赛跑中,路程S(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是( )
A.甲、乙两人的速度相同
B.甲先到达终点
C.乙用的时间短
D.乙比甲跑的路程多
B
3、
小芳的爷爷每天坚持体育锻炼,某天他慢步行走到离家较远的公园,打了一会儿太极拳,然后沿原路跑步到家里,下面能够反映当天小芳爷爷离家的距离y(米)与时间x(分钟)之间的关系的大致图象是( )
C
A B C D
有下列说法:
①“龟兔再次赛跑”的路为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .
(把你认为正确说法的序号都填上)
4、
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了
“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的
时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).
①③④
(1)当用电量是180千瓦时时,电费
是 元;
(2)第二档的用电量范围是 ;
(3)“基本电价”是 元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
5、
为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如右折线图,请根据图像回答下列问题;
108
180
500千瓦时
结 束
小结:
函数有哪些表示法?
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
