安徽省涡阳县王元中学2019-2020学年第二学期九年级第一次月考数学试卷(含答案)
文档属性
| 名称 | 安徽省涡阳县王元中学2019-2020学年第二学期九年级第一次月考数学试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 560.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-02 15:42:39 | ||
图片预览



文档简介
2019—2020学年度第二学期九年级质量检测试卷(一)
数学
注意事项:
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列事件中的不可能事件是( )
A.三角形的两个内角的和小于第三个内角
B.未来3天内将下雨
C.经过交通信号灯的路口遇到红灯
D.三根长度分别为2cm、3cm、5cm的木棒摆成三角形
2.二次函数y=2x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
A.y=2x2+3 B.y=-2x2+3 C.y=2(x-3)2 D.y=-2(x-3)2
3.如图所示的几何体,从上边看得到的图形是( )
4.如图,一个小球由地面沿着坡角为30°的坡面向上前进了10m,此时小球距离地面的
高度为( )
A.5m B.m
C. D.
5.下列说法中,不正确的是( )
A.圆既是轴对称图形又是旋转对称图形 B.一个圆的直径的长是它半径的2倍
C.圆的每一条直径都是它的对称轴 D.直径是圆的弦,但半径不是弦
6.如图,在△ABC中,点D,E分别在边AB,AC上,∠ADE=∠B,已知AE=6,,
则EC的长是( )
A.4.5 B.8 C.10.5 D.14
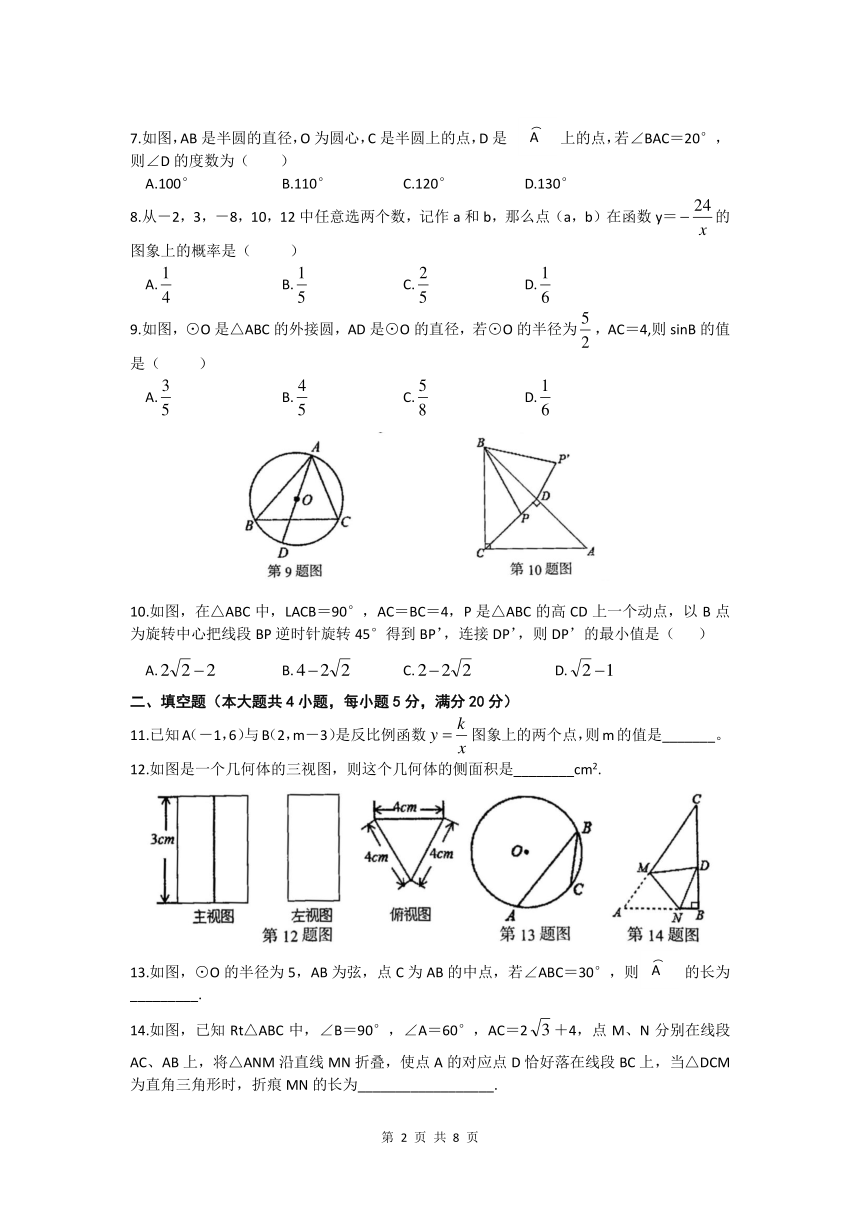
7.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BAC=20°,
则∠D的度数为( )
A.100° B.110° C.120° D.130°
8.从-2,3,-8,10,12中任意选两个数,记作a和b,那么点(a,b)在函数y=的图象上的概率是( )
A. B. C. D.
9.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为,AC=4,则sinB的值是( )
A. B. C. D.
10.如图,在△ABC中,LACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP’,连接DP’,则DP’的最小值是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知A(-1,6)与B(2,m-3)是反比例函数图象上的两个点,则m的值是_______。
12.如图是一个几何体的三视图,则这个几何体的侧面积是________cm2.
13.如图,⊙O的半径为5,AB为弦,点C为AB的中点,若∠ABC=30°,则 的长为_________.
14.如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__________________.
三、(本大题共两小题,每小题8分,共16分)
15.计算:
16.在平面直角坐标系中,二次函数的图象交坐标轴于A(-2.0),B(4,0),C(1,3)三点。求这个二次函数的解析式。
四、(本大题共两小题,每小题10分,共20分)
17.有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y)。
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=图象上的概率。
18.如图,在平面直角坐标系xoy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),
C(-5,2)。
(1)将△ABC绕着O顺时针旋转90°得到△A1B1C1,请画出△A1B1C1,并写出A1的坐标;
(2)以原点O为位似中心,在第一象限画出△A1B1C1的位似图形△A2B2C2,相似比为1:2,并写出A2的坐标。
五、(本大题共两小题,每小题12分,共24分)
19.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求v关于t的函数表达式;
(2)方方上午8点驾驶小汽车从A地出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围;
②方方能否在当天11点30分前到达B地?说明理由.
20.如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物一部分(把汽车看成一个点),这时视线与公路夹角为30°;
(1)汽车行驶到什么位置时,司机刚好看不到甲建筑物?请在图中标出这个D点;
(2)若CF的高度40米,当刚好看不到甲建筑物时,司机的视线与与公路夹角为45°,请问汽车行驶了多少米?
六、(本题12分)
21.在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃3、4、5三张牌,小明先抽一张,记录后放回,小刚再从3张中随机抽一张,若两张牌上的数字之积是奇数,则小明看电影,否则小刚看电影,乙的方案公平吗?请说明理由.
七、(本题12分)
22.如图,△ABC内接于⊙O,AB为直径,作OD⊥AB交AC于点D,延长BC,OD交于点F,过点C作OO的切线CE,交OF于点E.
(1)求证:EC=ED;
(2)如果OA=4,EF=3,求弦AC的长.
八、(本题14分)
23.超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件,设销售单价增加x元,每天售出y件.
(1)请写出y与x之间的函数表达式;
(2)当x为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利w元,当x为多少时w最大,最大值是多少?
2019—2020学年度第二学期九年级质量检测试卷参考答案
数学
1-5.DCBAC 6-10.BBBBA
11.0 12.36 13. 14.或
15.【答案】解:
==4-1+9=12.
16.【答案】由题意得,此二次函数的顶点为C(1,3),所以设此函数的解析式为,∵图象过点B(4, 0),∴,;.
17.【答案】解:(1)根据题意,可以画出如下的树状图:
则点A所有可能的坐标有:(1,﹣1)、(1,0)、(1,2)、(﹣2,﹣1)、(﹣2,0)、(﹣2,﹣2);
(2)在反比例函数y=图象上的坐标有:(1,2)、(﹣2,﹣1),
所以点A在反比例函数y=图象上的概率为:.
18.【答案】(1)如图,△A1B1C1是所画的图形,A1(4,2);
(2)如图,△A2B2C2是所画的图形,A2(8,4).
19.【解答】(1)根据题意,得vt=480,所以,因为,所以当时,,
综上,v关于t的函数表达式为;
(2)①根据题意,得,当t=4.8时,v=10;当t=6时,v=8.
∴小汽车行驶速度v的范围是;
②方方不能在11点30分前到达B地.理由如下:法一:若方方要在11点30分前到达B地,则,
所以,所以方方不能在11点30分前到达B地;
20.【答案】解:(1)如图所示:汽车行驶到点位置D时,司机刚好看不到建筑物B;
设CF=x米,∵CF⊥AE,∠CDF=45°,∴tan45°=∴DF=CF=40m.
∵∠A=30°,tan30°==,∴AF=40,∴AD=AF﹣DF=(40﹣40)m.
则他向前行驶了(40﹣40)米.
21.【答案】解:(1)甲同学的方案不公平.理由如下:列表法,
小明 小刚 2 3 4 5
2 (2,2) (2,3) (2,4) (2,5)
3 (3,2) (3,4) (3,5)
4 (4,2) (4,3) (4,5)
5 (5,2) (5,3) (5,4)
所有可能出现的结果共有12种,其中抽出的牌面上的数字之和为奇数的有:8种,故小明获胜的概率为:=,则小刚获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平;
(2)不公平.理由如下:
小明 小刚 3 4 5
3 (3,3) (3,4) (3,5)
4 (4,3) (4,4) (4,5)
5 (5,3) (4,5) (5,5)
所有可能出现的结果共有9种,其中抽出的牌面上的数字之积为奇数的有:4种,故小明获胜的概率为:,则小刚获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平.
22.【答案】解:(1)证明:连接OC,
∵CE与⊙O相切,OC是⊙O的半径,∴OC⊥CE,∴∠OCA+∠ACE=90°.
∵OA=OC,∴∠A=∠OCA,∴∠ACE+∠A=90°.
∵OD⊥AB,∴∠ODA+∠A=90°.又∵∠ODA=∠CDE,∴∠CDE+∠A=90°.
∴∠CDE=∠ACE,∴EC=ED.
(2)解:∵AB为直径,∴∠ACB=90°.
在Rt△DCF中,∠DCE+∠ECF=90°,又∠DCE=∠CDE,
∴∠CDE+∠ECF=90°,又∵∠CDE+∠F=90°,
∴∠ECF=∠F,∴EC=EF.
∵EF=3,∴EC=DE=3.在Rt△OCE中,OC=4,CE=3,
∴OE===5.
∴OD=OE-DE=2.
在Rt△OAD中,AD===.
在Rt△AOD和Rt△ACB中,∵∠A=∠A,∴Rt△AOD∽Rt△ACB,
∴,即,∴AC=.
23.【答案】解: (1);
(2)由题意得(50-)(40+x)=2250
解得x1=10,x2=50,因为x+40≤60,所以x≤20.所以x=10.
(3)w=(50-)(40+x)=(x-30)2+2450
因为<0,所以当x<30时,w随x的增大而增大,因为0所以x=20时,w最大=2400元.
数学
注意事项:
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,共40分)
1.下列事件中的不可能事件是( )
A.三角形的两个内角的和小于第三个内角
B.未来3天内将下雨
C.经过交通信号灯的路口遇到红灯
D.三根长度分别为2cm、3cm、5cm的木棒摆成三角形
2.二次函数y=2x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
A.y=2x2+3 B.y=-2x2+3 C.y=2(x-3)2 D.y=-2(x-3)2
3.如图所示的几何体,从上边看得到的图形是( )
4.如图,一个小球由地面沿着坡角为30°的坡面向上前进了10m,此时小球距离地面的
高度为( )
A.5m B.m
C. D.
5.下列说法中,不正确的是( )
A.圆既是轴对称图形又是旋转对称图形 B.一个圆的直径的长是它半径的2倍
C.圆的每一条直径都是它的对称轴 D.直径是圆的弦,但半径不是弦
6.如图,在△ABC中,点D,E分别在边AB,AC上,∠ADE=∠B,已知AE=6,,
则EC的长是( )
A.4.5 B.8 C.10.5 D.14
7.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BAC=20°,
则∠D的度数为( )
A.100° B.110° C.120° D.130°
8.从-2,3,-8,10,12中任意选两个数,记作a和b,那么点(a,b)在函数y=的图象上的概率是( )
A. B. C. D.
9.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为,AC=4,则sinB的值是( )
A. B. C. D.
10.如图,在△ABC中,LACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP’,连接DP’,则DP’的最小值是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知A(-1,6)与B(2,m-3)是反比例函数图象上的两个点,则m的值是_______。
12.如图是一个几何体的三视图,则这个几何体的侧面积是________cm2.
13.如图,⊙O的半径为5,AB为弦,点C为AB的中点,若∠ABC=30°,则 的长为_________.
14.如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__________________.
三、(本大题共两小题,每小题8分,共16分)
15.计算:
16.在平面直角坐标系中,二次函数的图象交坐标轴于A(-2.0),B(4,0),C(1,3)三点。求这个二次函数的解析式。
四、(本大题共两小题,每小题10分,共20分)
17.有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y)。
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=图象上的概率。
18.如图,在平面直角坐标系xoy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),
C(-5,2)。
(1)将△ABC绕着O顺时针旋转90°得到△A1B1C1,请画出△A1B1C1,并写出A1的坐标;
(2)以原点O为位似中心,在第一象限画出△A1B1C1的位似图形△A2B2C2,相似比为1:2,并写出A2的坐标。
五、(本大题共两小题,每小题12分,共24分)
19.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求v关于t的函数表达式;
(2)方方上午8点驾驶小汽车从A地出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围;
②方方能否在当天11点30分前到达B地?说明理由.
20.如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物一部分(把汽车看成一个点),这时视线与公路夹角为30°;
(1)汽车行驶到什么位置时,司机刚好看不到甲建筑物?请在图中标出这个D点;
(2)若CF的高度40米,当刚好看不到甲建筑物时,司机的视线与与公路夹角为45°,请问汽车行驶了多少米?
六、(本题12分)
21.在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃3、4、5三张牌,小明先抽一张,记录后放回,小刚再从3张中随机抽一张,若两张牌上的数字之积是奇数,则小明看电影,否则小刚看电影,乙的方案公平吗?请说明理由.
七、(本题12分)
22.如图,△ABC内接于⊙O,AB为直径,作OD⊥AB交AC于点D,延长BC,OD交于点F,过点C作OO的切线CE,交OF于点E.
(1)求证:EC=ED;
(2)如果OA=4,EF=3,求弦AC的长.
八、(本题14分)
23.超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件,设销售单价增加x元,每天售出y件.
(1)请写出y与x之间的函数表达式;
(2)当x为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利w元,当x为多少时w最大,最大值是多少?
2019—2020学年度第二学期九年级质量检测试卷参考答案
数学
1-5.DCBAC 6-10.BBBBA
11.0 12.36 13. 14.或
15.【答案】解:
==4-1+9=12.
16.【答案】由题意得,此二次函数的顶点为C(1,3),所以设此函数的解析式为,∵图象过点B(4, 0),∴,;.
17.【答案】解:(1)根据题意,可以画出如下的树状图:
则点A所有可能的坐标有:(1,﹣1)、(1,0)、(1,2)、(﹣2,﹣1)、(﹣2,0)、(﹣2,﹣2);
(2)在反比例函数y=图象上的坐标有:(1,2)、(﹣2,﹣1),
所以点A在反比例函数y=图象上的概率为:.
18.【答案】(1)如图,△A1B1C1是所画的图形,A1(4,2);
(2)如图,△A2B2C2是所画的图形,A2(8,4).
19.【解答】(1)根据题意,得vt=480,所以,因为,所以当时,,
综上,v关于t的函数表达式为;
(2)①根据题意,得,当t=4.8时,v=10;当t=6时,v=8.
∴小汽车行驶速度v的范围是;
②方方不能在11点30分前到达B地.理由如下:法一:若方方要在11点30分前到达B地,则,
所以,所以方方不能在11点30分前到达B地;
20.【答案】解:(1)如图所示:汽车行驶到点位置D时,司机刚好看不到建筑物B;
设CF=x米,∵CF⊥AE,∠CDF=45°,∴tan45°=∴DF=CF=40m.
∵∠A=30°,tan30°==,∴AF=40,∴AD=AF﹣DF=(40﹣40)m.
则他向前行驶了(40﹣40)米.
21.【答案】解:(1)甲同学的方案不公平.理由如下:列表法,
小明 小刚 2 3 4 5
2 (2,2) (2,3) (2,4) (2,5)
3 (3,2) (3,4) (3,5)
4 (4,2) (4,3) (4,5)
5 (5,2) (5,3) (5,4)
所有可能出现的结果共有12种,其中抽出的牌面上的数字之和为奇数的有:8种,故小明获胜的概率为:=,则小刚获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平;
(2)不公平.理由如下:
小明 小刚 3 4 5
3 (3,3) (3,4) (3,5)
4 (4,3) (4,4) (4,5)
5 (5,3) (4,5) (5,5)
所有可能出现的结果共有9种,其中抽出的牌面上的数字之积为奇数的有:4种,故小明获胜的概率为:,则小刚获胜的概率为:,
故此游戏两人获胜的概率不相同,即他们的游戏规则不公平.
22.【答案】解:(1)证明:连接OC,
∵CE与⊙O相切,OC是⊙O的半径,∴OC⊥CE,∴∠OCA+∠ACE=90°.
∵OA=OC,∴∠A=∠OCA,∴∠ACE+∠A=90°.
∵OD⊥AB,∴∠ODA+∠A=90°.又∵∠ODA=∠CDE,∴∠CDE+∠A=90°.
∴∠CDE=∠ACE,∴EC=ED.
(2)解:∵AB为直径,∴∠ACB=90°.
在Rt△DCF中,∠DCE+∠ECF=90°,又∠DCE=∠CDE,
∴∠CDE+∠ECF=90°,又∵∠CDE+∠F=90°,
∴∠ECF=∠F,∴EC=EF.
∵EF=3,∴EC=DE=3.在Rt△OCE中,OC=4,CE=3,
∴OE===5.
∴OD=OE-DE=2.
在Rt△OAD中,AD===.
在Rt△AOD和Rt△ACB中,∵∠A=∠A,∴Rt△AOD∽Rt△ACB,
∴,即,∴AC=.
23.【答案】解: (1);
(2)由题意得(50-)(40+x)=2250
解得x1=10,x2=50,因为x+40≤60,所以x≤20.所以x=10.
(3)w=(50-)(40+x)=(x-30)2+2450
因为<0,所以当x<30时,w随x的增大而增大,因为0
