2019-2020学年八年级下册第十九章一次函数同步练习:19.3《课题学习 选择方案》(解析版)
文档属性
| 名称 | 2019-2020学年八年级下册第十九章一次函数同步练习:19.3《课题学习 选择方案》(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 206.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-02 17:28:31 | ||
图片预览



文档简介
2020年春八年级下册同步练习:19.3《课题学习 选择方案》
一.选择题(共6小题)
1.某公司为调动职工工作积极性,向工会代言人提供了两个加薪方案,要求他从中选择:
方案一:是12个月后,在年薪20000元的基础上每年提高500元(第一年年薪20000元);
方案二:是6个月后,在半年薪10000元的基础上每半年提高250元(第6个月末发薪水10000元)
但不管是选哪一种方案,公司都是每半年发一次工资,如果你是工会代言人,认为哪种方案对员工更有利?( )
A.方案一 B.方案二
C.两种方案一样 D.工龄短的选方案一,工龄长的选方案二
2.某地为了改善生态环境,政府决定绿化荒山,计划第一年先植树0.5万公顷,以后每年比上年增加1万公顷,结果植树面积y(万公顷)是时间x(年)的一次函数,这个函数图象是( )
A. B.
C. D.
3.声音在空气中传播的速度与气温的关系如下表:
气温T/℃ ﹣20 ﹣10 0 10 20 30
声速v/(m/s) 318 324 330 336 342 348
根据表格下列分析错误的是( )
A.在这个变化过程中,气温和声速都是变量
B.声速随气温的升高而增大
C.声速v与气温T的关系式为v=T+330
D.气温每升高10℃,声速增加6m/s
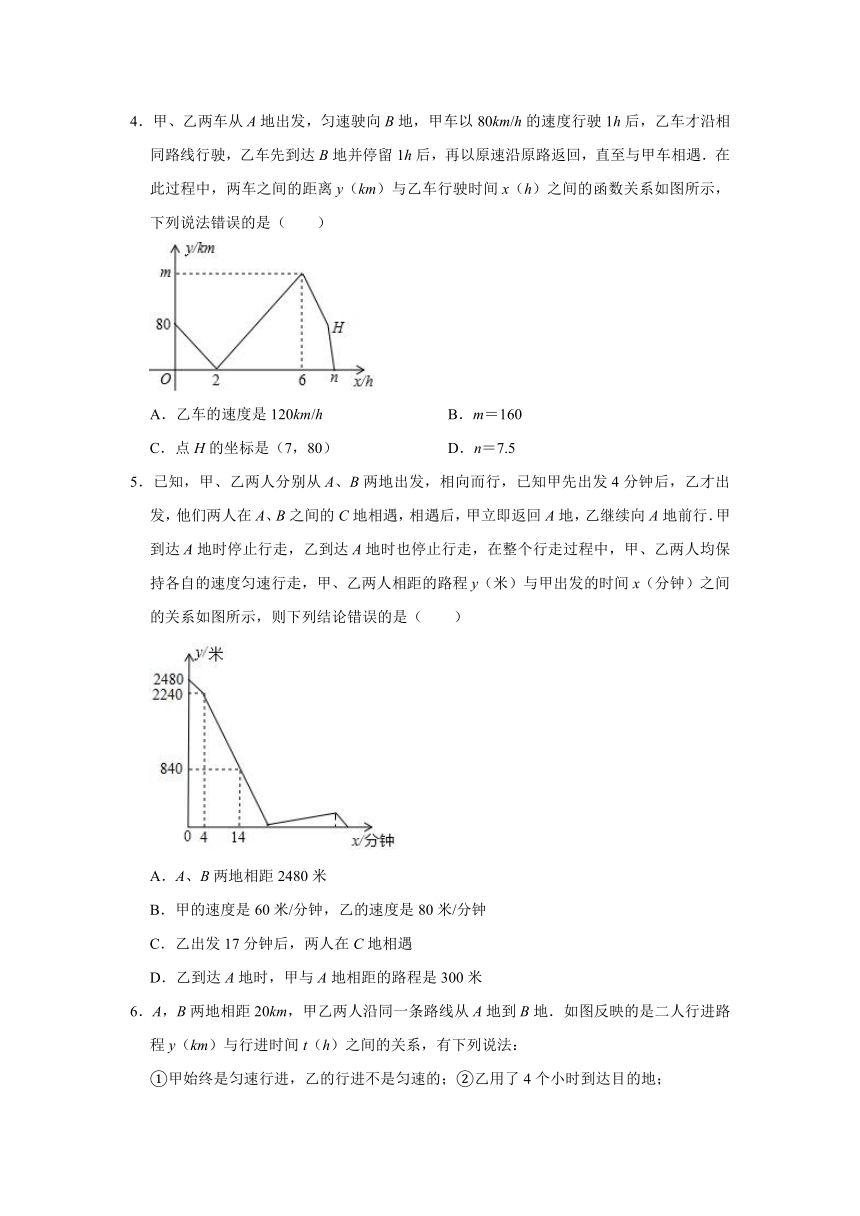
4.甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶,乙车先到达B地并停留1h后,再以原速沿原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示,下列说法错误的是( )
A.乙车的速度是120km/h B.m=160
C.点H的坐标是(7,80) D.n=7.5
5.已知,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发4分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则下列结论错误的是( )
A.A、B两地相距2480米
B.甲的速度是60米/分钟,乙的速度是80米/分钟
C.乙出发17分钟后,两人在C地相遇
D.乙到达A地时,甲与A地相距的路程是300米
6.A,B两地相距20km,甲乙两人沿同一条路线从A地到B地.如图反映的是二人行进路程y(km)与行进时间t(h)之间的关系,有下列说法:
①甲始终是匀速行进,乙的行进不是匀速的;②乙用了4个小时到达目的地;
③乙比甲先出发1小时;④甲在出发4小时后被乙追上.
在这些说法中,正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题)
7.如图,OA和BA分别表示甲、乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判定快者比慢者每秒多跑 米.
8.某市政府大力扶持大学生创业.小甬在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数:y=﹣10x+500.根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果小甬想要每月获得的利润不低于2000元,那么他每月的成本最少需要 元.(成本=进价×销售量)
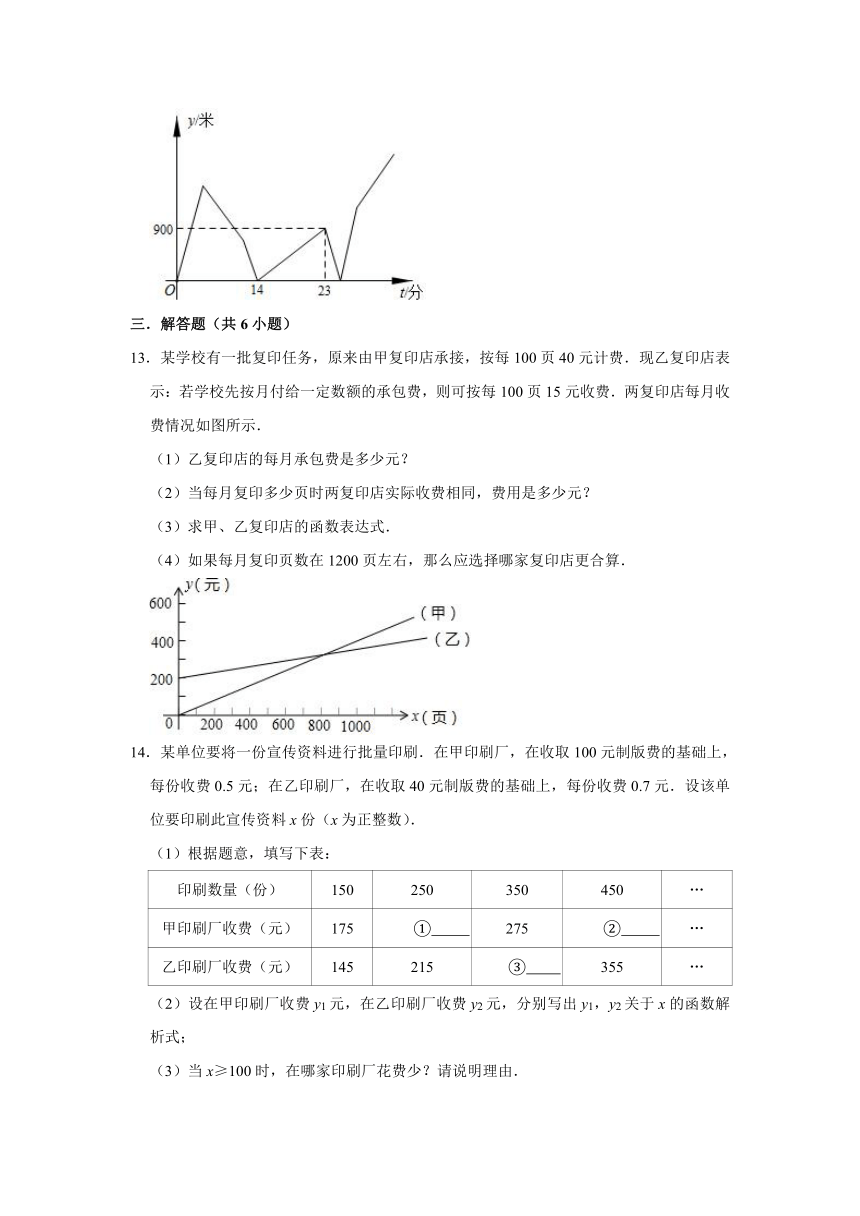
9.某快递公司每天上午9:30﹣10:30为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么从9:30开始,经过 分钟时,当两仓库快递件数相同.
10.小红从家到图书馆查阅资料然后返回,她离家的距离y与离家的时间x之间的对应关系如图所示,如果小红离家50分钟时离家的距离为0.3km,那么她在图书馆查阅资料的时间为 .
11.如图是某企业职工养老保险个人缴费y(元)随个人月工资x(元)变化的图象,请你根椐图象回答下列问题:
①张总工程师5月份工资是3000元,这个月他应缴个人养老保险费 元.
②小王5月份工资为500元,这个月他应缴个人养老保险费 元.
③当月工资在600?2800元之间时,个人养老保险费y(元)与月工资x(元)之间的函数关系式为 .
12.已知A、B、C三地顺次在同一直线上,甲、乙两人均骑车从A地出发,向C地匀速行驶.甲比乙早出发5分钟,甲到达B地并休息了2分钟后,乙追上了甲.甲、乙同时从B地以各自原速继续向C地行驶.当乙到达C地后,乙立即掉头并提速为原速的倍按原路返回A地,而甲也立即提速为原速的倍继续向C地行驶,到达C地就停止.若甲、乙间的距离y(米)与甲出发的时间t(分)之间的函数关系如图所示,则下列说法①甲、乙提速前的速度分别为300米/分、400米/分;②A、C两地相距7200米;③甲从A地到C地共用时26分钟;④当甲到达C地时,乙距A地6075米;其中正确的是 .
三.解答题(共6小题)
13.某学校有一批复印任务,原来由甲复印店承接,按每100页40元计费.现乙复印店表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印店每月收费情况如图所示.
(1)乙复印店的每月承包费是多少元?
(2)当每月复印多少页时两复印店实际收费相同,费用是多少元?
(3)求甲、乙复印店的函数表达式.
(4)如果每月复印页数在1200页左右,那么应选择哪家复印店更合算.
14.某单位要将一份宣传资料进行批量印刷.在甲印刷厂,在收取100元制版费的基础上,每份收费0.5元;在乙印刷厂,在收取40元制版费的基础上,每份收费0.7元.设该单位要印刷此宣传资料x份(x为正整数).
(1)根据题意,填写下表:
印刷数量(份) 150 250 350 450 …
甲印刷厂收费(元) 175 ① 275 ② …
乙印刷厂收费(元) 145 215 ③ 355 …
(2)设在甲印刷厂收费y1元,在乙印刷厂收费y2元,分别写出y1,y2关于x的函数解析式;
(3)当x≥100时,在哪家印刷厂花费少?请说明理由.
15.某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30时,求y与x之间的函数关系式;
(2)若小李4月份上网35小时,他应付多少元的上网费用?
16.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图象进行探究:
(1)甲、乙两地之间的距离为 km;
(2)请解释图中点B的实际意义: ;
(3)求线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
17.甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/kg.在乙批发店,一次购买数量不超过20kg时,价格为7元/kg;一次购买数量超过20kg时,其中有20kg的价格仍为7元/kg,超过20kg部分的价格为5元/kg.设小王在同一个批发店一次购买苹果的数量为xkg(x>0).
(Ⅰ)根据题意填空:
①若一次购买数量为10kg时,在甲批发店的花费为 元,在乙批发店的花费为 元;
②若一次购买数量为50kg时,在甲批发店的花费为 元,在乙批发店的花费为 元;
(Ⅱ)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数解析式;
(Ⅲ)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为 kg;
②若小王在同一个批发店一次购买苹果的数量为30kg,则他在甲、乙两个批发店中的 批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了260元,则他在甲、乙两个批发店中的 批发店购买数量多.
18.已知A地,火神山医院、B地顺次在一条笔直的公路上,且A地、B地距火神山医院的路程相同,甲、乙两家车队分别从A、B两地向火神山医院运送货物,甲车队比乙车队晚出发0.75小时.为避免拥堵,总调度部门通知距火神山医院更近的车队进工地卸货(卸货时间忽略不计),然后原路原速返回,而另一车队则在火神山医院40千米处等待直到另一车队卸货完毕后再按原速继续行驶进入工地,卸货后原路原速返回.甲车队距A地的路程y(千米)与甲车队行驶的时间x(小时)之间的函数关系如图所示:
(1)甲车队的速度为 千米/时,乙车队的速度为 千米/时,A地与火神山医院之间的距离为 千米.
(2)甲车队原路返回时y与x之间的函数关系式.
(3)直接写出两车队相距80千米时x的值.
参考答案
一.选择题(共6小题)
1.【解答】解:∵方案一:是12个月后,在年薪20000元的基础上每年提高500元(第一年年薪20000元),
∴按这种方案计算,第一年年薪为20000元,第二年年薪为20000+500=20500元,
∵方案二:是6个月后,在半年薪10000元的基础上每半年提高250元(第6个月末发薪水10000元),
∴按这种方案计算,第一年年薪为10000+(10000+250)=20250元,第二年年薪为(10000+500)+(10000+750)=21250元,
由上可知,方案二比方案一对员工更有利.
故选:B.
2.【解答】解:总面积y(万亩)是x的一次函数,y=x﹣0.5,
当x=1,y=0.5,x=2,y=1.5,
所以图象A符合题意.
故选:A.
3.【解答】解:在这个变化过程中,气温和声速都是变量,故选项A正确;
声速随气温的升高而增大,故选项B正确;
由表格可知,气温每升高10℃,速度增加6m/s,
设v=kT+b,
,得
故声速v与气温T的关系式为v=0.6T+330,故选项C错误;
气温每升高10℃,声速增加6m/s,故选项D正确;
故选:C.
4.【解答】解:由图象可知,乙出发时,甲乙相距80km,2小时后,乙车追上甲.则说明乙每小时比甲快40km,则乙的速度为120km/h.A正确;
由图象第2﹣6小时,乙由相遇点到达B,用时4小时,每小时比甲快40km,则此时甲乙距离4×40=160km,则m=160,B正确;
当乙在B休息1h时,甲前进80km,则H点坐标为(7,80),C正确;
乙返回时,甲乙相距80km,到两车相遇用时80÷(120+80)=0.4小时,则n=6+1+0.4=7.4,D错误.
故选:D.
5.【解答】解:由图象可知,A、B两地相距2480米,故选项A不合题意;
甲的速度为(2480﹣2240)÷4=60(米/分钟),
乙的速度为(2240﹣840)÷(14﹣4)﹣60=80(米/分钟),故选项B不合题意;
甲、乙相遇的时间为4+2240÷(60+80)=20(分钟),故选项C符合题意;
A、C两地之间的距离为60×20=1200(米),
乙到达A地时,甲与A地相距的路程为1200﹣1200÷80×60=300(米).故选项D不合题意.
故选:C.
6.【解答】解:由图象可得,
甲始终是匀速行进,乙的行进不是匀速的,刚开始一段时间匀速,后来提速,继续做匀速运动,故①正确;
乙用了3个小时到达目的地,故②错误;
乙比甲晚出发1小时,故③错误;
甲在出发4小时后被乙超过,故④错误;
由上可得,正确是①,
故选:A.
二.填空题(共6小题)
7.【解答】解:如图所示:快者的速度为:64÷8=8(m/s),
慢者的速度为:(64﹣12)÷8=6.5(m/s),
8﹣6.5=1.5(米),
所以快者比慢者每秒多跑1.5米.
故答案为:1.5
8.【解答】解:设成本为P(元),由题意,得:P=20(﹣10x+500)=﹣200x+10000,
∵a=﹣200<0,
∴P随x的增大而减小,
由∵x≤32,
∴当x=32时,P最小=3600,
答:想要每月获得的利润不低于2000元,每月的成本最少为3600元.
故答案为:
9.【解答】解:设甲仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y1=k1x+40,根据题意得60k1+40=400,解得k1=6,
∴y1=6x+40;
设乙仓库的快件数量y(件)与时间x(分)之间的函数关系式为:y2=k2x+240,根据题意得60k2+240=0,解得k2=﹣4,
∴y2=﹣4x+240,
联立,
解得,
∴经过20分钟时,当两仓库快递件数相同.
故答案为:20
10.【解答】解:设她返回时距离y与离家的时间x之间的函数解析式为y=kx+b,
∵小红离家50分钟时离家的距离为0.3km,
∴,
解得:∴y=﹣x+3.3,
当y=0.9时,x=40,
40﹣10=30,
答:她在图书馆查阅资料的时间为30分钟.
故答案为:30分钟.
11.【解答】解:(1)根据图象可知当x≥2800时,y=200,
∴张总工程师五月份工资3000元,这个月他个人应缴养老保险200元;
(2)根据图象可知当350≤x≤600时,y=40;
∴小王5月份工资500元,这月他应缴养老保险40元;
(3)设工资在600?2800元之间所交养老保险金的函数关系式为y=kx+b(k≠0),
,解得,
∴个人养老保险费y(元)与月工资x(元)之间的函数关系式为.
故答案为:(1)200;(2)40;(3).
12.【解答】解:由题意可得,
甲乙两人刚开始的速度之差为:900÷(23﹣14)=100(米/分),
设甲刚开始的速度为x米/分,乙刚开始的速度为(x+100)米/分,
12x=(14﹣5)×(x+100),
解得,x=300,
则x+100=400,
即甲、乙提速前的速度分别为300米/分、400米/分.故①正确;
A、B两地之间的距离为:300×12=3600(米),
A、C两地之间的距离为:400×(23﹣5)=7200(米),故②正确;
∵当乙到达C地后,乙立即掉头并提速为原速的倍按原路返回A地,而甲也立即提速为原速的倍继续向C地行驶,
∴后来乙的速度为:400×=500(米/分),甲的速度为300×=400(米/分),
∴甲从A地到C地共用时:23+[7200﹣(23﹣2)×300]÷400=25(分钟),故③错误;
∴当甲到达C地时,乙距A地:7200﹣(25﹣23)×500=6075(米),故④正确.
综上所述,正确的有①②④.
故答案为:①②④
三.解答题(共6小题)
13.【解答】解:(1)x=0时,y=200,乙复印店的每月承包费是200元.
(2)设复印x页时两复印店实际收费相同,
由题意0.4x=200+0.15x,
解得x=800.
0.4×800=320(元),
答:当每月复印800页时两复印店实际收费相同,费用是320元;
(3),,
y甲=0.4x,
y乙=0.15x+200;
(4)当x=1200时,
y甲=0.4×1200=480(元),
y乙=0.15×1200+200=380(元).
∵480元>380元,
∴如果每月复印页数在1200页左右,那么应选择乙家复印店更合算.
14.【解答】解:(1)由题意可得,
当x=250时,甲印刷厂的费用为:100+0.5×250=225(元),
当x=450时,甲印刷厂的费用为:100+0.5×450=325(元),
当x=350时,乙印刷厂的费用为:40+0.7×350=285(元),
故答案为:①225;②325;③285.
(2)根据题意,得y1=100+0.5x,y2=40+0.7x.
(3)设在甲、乙两个印刷厂收费金额的差为y元,则y=y1﹣y2=60﹣0.2x.
当y=0时,即60﹣0.2x=0,得x=300.
∴当x=300时,在甲、乙两个印刷厂花费相同.
∵﹣0.2<0,
∴y随x的增大而减小.
∴当100≤x<300时,有y>0,在乙印刷厂花费少;
当x>300时,有y<0,在甲印刷厂花费少.
15.【解答】解:(1)设当x≥30时,y与x之间的函数关系式是y=kx+b,
,
解得,,
即当x≥30时,y与x之间的函数关系式是y=3x﹣30;
(2)当x=35时,
y=3×35﹣30=105﹣30=75,
即小李4月份上网35小时,他应付75元的上网费用.
16.【解答】解:(1)由题意,得
甲、乙两地之间的距为900km.
故答案为:900;
(2)由函数图象,得图中点B的实际意义是:当慢车行驶4 h时,慢车和快车相遇.
故答案为:当慢车行驶4 h时,慢车和快车相遇;
(3)设线段CD的解析式为y=kx+b,
快车与慢车的速度和为:900÷4=225(km/h),
慢车的速度为:900÷12=75(km/h),
快车的速度为:225﹣75=150( km/h).
由题意,得快车走完全程的时间按为:900÷150=6h,
6时时两车之间的距离为:225×(6﹣4)=450km.
则C(6,450).
将点C(6,450)、D(12,900)代入函数关系式得
,解得,
∴线段CD的解析式为y=75x(6≤x≤12).
17.【解答】解:(I)①根据题意得,
在甲批发店的花费为:6×10=60(元),
在乙批发店的花费为:7×10=70(元);
故答案为:60;70;
②根据题意得,
在甲批发店的花费为:6×50=300(元);
在乙批发店的花费为:7×20+5×(50﹣20)=290(元);
故答案为:300;290;
(II)根据题意得,
y1=6x(x>0);
当0<x≤20时,y2=7x;
当x>20时,y2=7×20+5(x﹣20)=5x+40.
即;
(III)①设他在同一个批发店一次购买苹果的数量为xkg,根据题意得
6x=7×20+5(x﹣20),
解得,x=40,
故答案为40;
②在甲店的花费为:6×30=180(元),
在乙店的花费为:7×20+5×(30﹣20)=190(元),
则在甲店批发购买花费较少,
故答案为:甲;
③在甲店购买苹果数量为:260÷6=(kg),
设在乙店购买苹果数量为ykg,由题意得,
5x+40=260,
解得,x=44(kg),
则在乙店批发购买的苹果数量较多.
故答案为:乙.
18.【解答】解:(1)设甲车队速度为v甲千米/时,v甲×1+40=v甲(3.25﹣1.75),v甲=80,
80+40=120千米.
v乙=120÷[1.75﹣(3.25﹣1.75)+1+0.75]=60(千米/时),
故答案为:80;60;120.
(2)设甲车队返回时一次函数为y=kx+b.有,
解得k=﹣80,b=260,
∴y=﹣80x+260.
(3)在乙车队没有到达火神山医院前,有80x+60(x+0.75)=240﹣80,解得x=;
在甲车队卸货结束后,有80(x﹣1.75)+60(x﹣1.75+40÷80)=80,解得x=.
即两车队相距80千米时x的值为或.
